
信号検出理論の説明(type 2 と meta-d')
type 2 とは?
信号検出理論では type 1 の課題(以下 type 1 task)に続く形で type 2 の課題(以下 type 2 task)が存在する。
2者の違いを一言で表すと,type 1 task が signal の有無を判断するものだったのに対して,type 2 task はその判断に対する確信度(その判断が正しいという自信)を評価するものである。
この確信度評価は,特に心理学の領域においては「メタ認知」能力を測る際に使用されることが多く,この評価では主に「低 or 高」の2値や「(低い)1 〜 6(高い)」のようなスケールが用いられる。
(メタ認知: 認知の認知。自分の認知を一歩離れたところから観察するというセルフモニタリング能力)
メタ認知の例
メタ認知能力が高い人は type 1 task の結果が正解の試行では確信度を高く,誤りの試行では確信度を低く評価する,すなわち,自分の判断の正誤を自分の中で明確に区別できていると考えられる。
日常生活での例を考えてみると,ある犯罪現場を目撃したとして,後ほど警察から複数人の写真を見せられて「この中に現場にいた人はいますか?」と聞かれたとする。
目撃者のメタ認知能力が高い場合は「絶対この人です」や「この人は確実にいませんでした」と断言され,その証言は信用に値すると考えられる。対照的に,メタ認知能力が低い場合は「多分この人だったような…」のような曖昧な証言となるか,「絶対この人です」と証言した場合でもそれが誤りである危険度が高い。
メタ認知能力を算出する方法
メタ認知能力を算出するには以下の 4 つの方法が考えられる。ただし,今日では重大な欠点や考慮すべき問題点が指摘されているものもあり,現実的な方法は 2 つであることには注意されたい。
① 正誤判断の結果と確信度との相関を見る
最も単純な方法は,正誤判断の結果とその確信度との相関を見ることである。
例えば type 1 task での正解を1,誤りを0とすると,[1, 0, 0, 1, 1, 1, 0, 1, …] といった各試行での正誤を示す配列を得ることができる。さらに,各試行での判断に対して確信度の評価が行われるため,高確信度を1,低確信度を0とすると,上と同様に [0, 1, 0, 1, 1, 1, 0, 0, …] といった配列を得ることができる。
よって,得られた正誤判断の結果と確信度評価との相関を見ることができ,これをメタ認知能力の指標とみなす。この方法でのメタ認知能力の指標には "φ" が使用されるが,算出方法を考えるとピアソンの積率相関係数 "r" と同じことを意味する。また,このほかに "G" という指標も存在するが,こちらは確信度を「低 or 高」の2値ではなく「(低い)1 〜 6(高い)」のようなスケールで評価した場合に採用される。
これは非常に簡単な方法であるが,単純な相関を見るだけではメタ認知能力とメタ認知的バイアスとを区別することができない。
例えば,評価者が謙虚な人物で判断の正誤に関係なく確信度を低めに評価するような場合や,対照的に自信過剰で確信度を高めに評価する傾向がある場合を考える。これらの場合は判断の正誤と確信度との相関が小さくなるため,メタ認知能力が低いという結果になる。
このように,評価される確信度には評価者の持つ確信度判断の基準が影響するため,算出された指標がメタ認知能力を反映しているとは言い切れない。
専門的に言えば,この方法で算出される指標は contaminated である。
② type 2 d'を算出する
①の方法で指摘されたメタ認知的バイアスを考慮するために,type 1 task で使用された弁別力と反応バイアスとを独立に算出する方法を流用するというものである。
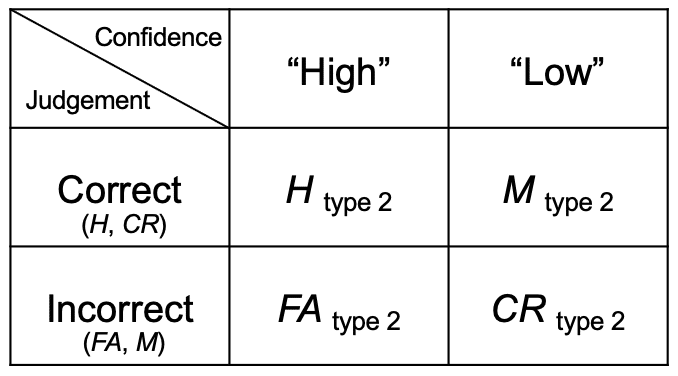
計算方法は type 1 task の場合と同様であるため,初めに type 2 の Hit 率と type 2 の False Alarm 率を算出する。これら(および type 2 の Miss 率と type 2 の Correct Rejection 率)は以下の通りであるが,表1を参考にされたい。
type 2 Hit: type 1 Hit と type 1 CR で確信度が高いもの
type 2 FA: type 1 FA と type 1 Miss で確信度が高いもの
type 2 Miss: type 1 Hit と type 1 CR で確信度が低いもの
type 2 CR: type 1 FA と type 1 Miss で確信度が低いもの
しかしながら,この方法には分布の仮定が満たされないという致命底な問題がある。
信号検出理論における d' 算出においては,N 分布と S + N 分布が等分散かつ正規分布に従うことが前提となっている。しかしながら,type 1 でこの仮定が満たされた場合,type 2 においては N 分布と S + N 分布とは等分散ではなく,また正規分布に従わないことがわかっている。
すなわち,type 2 d' は不適切な指標であり,メタ認知能力を示すことはできない。
③ type 2 ROC 曲線を使用する
②の問題であった分布の仮定に縛られないノンパラメトリックな方法である。
バイアスフリーである type 2 ROC 曲線下面積(AUROC2: area under the type 2 receiver operating characteristics curve)を算出すれば,これをメタ認知能力を示す指標として使うことができる。
type 2 ROC 曲線は type 1 ROC 曲線と同じように描くことができる。例えば,確信度が 1–6 のスケールで評価される場合を考える。初めに,「1 を Low で 2–6 を High」として上のマトリックスを作る。続いて,「1–2 を Low で 3–6 を High」,「1–3 を Low で 4–6 を High」,… と確信度の高低の基準を変化させていき,最後に「1–5 を Low で 6 を High」として計算する。これによって,type 2 の p(FA)・p(H)の座標上に 5 つの点を打つことができるので,これをつなぐように曲線を描く(詳細は type 1 ROC 曲線の描き方を調べられたい)。
注意点として,①,②の場合も同様であるが,AUROC2 は type 1 task のパフォーマンスの影響を受けることを考慮する必要がある。
例えば,中程度のメタ認知能力を持つ人物が難易度が極端に低い type 1 task に参加することを考える。この場合は正誤判断の正答率が高くなり,それに合わせて確信度も高くなることで,結果としてメタ認知能力が高いと判断されることが予想される。
また,AUROC2 は type 1 の c の影響も受けるが,これはモチベーションなどによっても容易に変化する。
よって,AUROC2 はメタ認知能力の指標として使用すること自体は問題ないが,その場合は type 1 task のパフォーマンスの影響を十分に考慮する必要がある。
(type 1 task のパフォーマンスを考慮するには,群間比較であれば,階層的重回帰分析や共分散分析などを使うという方法が考えられ,一部の研究でもこれを採用したものがある)
④ meta-d'を算出する
こちらは d' と同じ単位であるため,d' との差や比を直接考えることができるというものである。算出用のプログラムが公開されているため,使用される場合は参考文献 [1] を参照されたい。
ここでは,meta-d' がどのようなものであるのかを簡単に説明する。
結論としては,meta-d' とは「推定された d'」である。
押さえておきたいことは,type 2 ROC 曲線は type 1 の d' と c によって形が変わる(すなわち,type 1 のパフォーマンスの影響を受ける)ということであるが,これは,メタ認知的に ideal(完璧なメタ認知)であれば type 2 ROC 曲線はその曲線下面積を最大にするように描かれるため,type 1 の d' と c が与えられることで type 2 ROC 曲線はただ1つに決定することを意味する。詳細は参考文献 [2] を参照されたい。
この考えの下で,meta-d' を求める。
(これ以降,type 1 の指標の場合は "type 1"は省略して記述する)
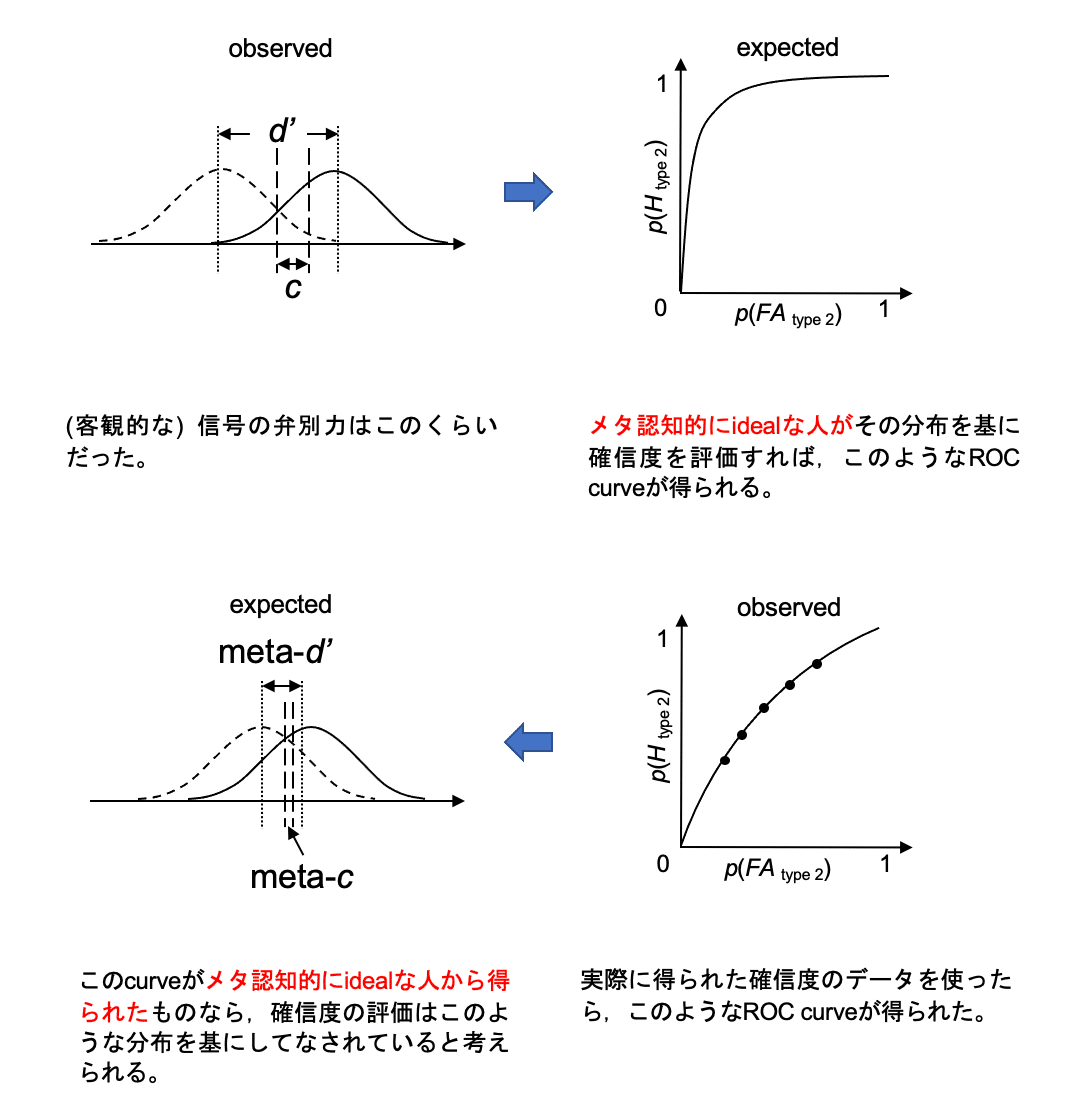
まず,ある参加者が実験に参加して,d' と c が得られたとする(observed d' & c)(図1左上)。
ここで,この参加者が仮にメタ認知的に ideal であったと仮定すると,得られた d' と c からただ 1 つの type 2 ROC 曲線を得ることができる(expected type 2 ROC curve)ことを考える(図1右上)。
(無数の type 2 ROC 曲線がある中で,メタ認知的に ideal だとすれば,後は d' と c がわかれば type 2 ROC 曲線が 1 つに定まるため)
その後,実際の確信度評価によって③記載の方法で,1 つの type 2 ROC 曲線が得られる(observed type 2 ROC curve)(図1右下)。
先述したこと(無数の〜定まる)を利用して,この observed type 2 ROC curve がメタ認知的に ideal な人物から得られたものであった仮定すると,その d' と c を推定することができるが,この推定された d' と c がそれぞれ meta-d', meta-c と呼ばれる(図1左下)。
meta-d' を用いてメタ認知能力を評価する際には,例えば meta-d'/d'(この比は M-ratio と呼ばれる)を計算することで,実際の type 1 のパフォーマンスと推定されたtype 1 のパフォーマンスとのズレを見ることができる。
M-ratio が 1 の場合は完璧なメタ認知であることを意味し,1 より小さくなるほどメタ認知能力が低いことを意味する。1 より大きい場合は自信過剰であるか,確信度評価の際に自分の正誤判断プロセス以外の情報を利用したと考えられる。
すなわち,例えば meta-d'<d' の場合は,「見たところ d' 程度の弁別ができているようだが,実際にはその人の中では meta-d' 程度の弁別しかできていない。つまり,自分の正誤判断に対するモニタリングが完璧ではなく,そのズレが大きいほど(M-ratioが小さいほど)メタ認知能力が低いことを表す」というものである。
イメージとしては,例えば 10 問各 1 点のテストがあったとすると,「テスト結果は 10 点だったが,実は 3 問は勘で答えたので実際には(頭の中では)7 点分しかわからなかった」という感じ。ここでのテスト結果が d 'で,頭の中が meta-d' にあたる。
この理解が難しい最大の理由は,実際にはメタ認知的に ideal ではないのにも関わらず,計算の中ではメタ認知的に ideal であることを仮定する点であると思われる。
これは表現を変えて,「その人が持っている弁別力を100%発揮したと考える(← この分の判断は自分の中で明確に区別できる)」と言えばわかりやすいかもしれない。
例えば,d' = 2 の弁別力を持った人の type 1 task の結果が d' = 3 であった場合を考える。この場合,差分 1 は勘やカンニングなど,その人の持つ弁別力以外の要素が関係したと考えられるが,expexted type 2 ROC curve は d' = 3 の弁別力が最大限に発揮された結果の形として描かれる。しかしながら,この人は d' = 2 の弁別力しか持っていないので,observed type 2 ROC curve は expected type 2 ROC curve とは異なる形になる。ここで,この人が持つ d' = 2 分の弁別力は最大限に発揮されていたと考えると,observed type 2 ROC curve から meta-d' = 2 という結果を推定することができる。
すなわち,一見すると d' = 3 程度の区別ができたという結果であったが,実はこの人の中では d' = 2 程度の区別しかできていなかった。しかしながら,この d' = 2 程度の区別は自分の中でもきちんと把握できていたと考えられるので(← これが meta-d'),type 1 task の結果としての弁別力 d' と推定された弁別力(この人が実際に持つ弁別力)meta-d' とを比較することで,自分の判断がどれだけ区別できているのか,そのズレがわかる,というものである。
(M-ratio を使用しても type 1 task のパフォーマンスの影響を完全に取り除くことはできないという指摘を何かの文献で見かけたと記憶しているが,出典不明であるためメモ書きに留める)
まとめ
信号検出理論を用いてメタ認知能力を評価することができる。ただし,type 1 task のパフォーマンスを十分に考慮する必要がある。
参考文献
Fleming, S. M., & Lau, H. C. (2014). How to measure metacognition. Frontiers in Human Neuroscience, 8:443. https://doi.org/10.3389/fnhum.2014.00443
Galvin, S. J., Podd, J. V., Drga, V., & Whitmore, J. (2003). Type 2 tasks in the theory of signal detectability: Discrimination between correct and incorrect decisions. Psychonomic Bulletin & Review, 10(4), 843–876. https://doi.org/10.3758/bf03196546
