
NIRSの信号処理について考えてみる〜③フーリエ変換〜
本記事では,前回登場した「フーリエ変換」について説明する。ただし,ここでは原理や厳密な計算などには触れず,実際の使い方とこれによって何がわかるのかに焦点を当てて簡単に記述する。
フーリエ変換とは?
厳密には誤りであるかもしれないが,フーリエ変換とは,簡単に言えば「あらゆる波は三角関数の和で表すことができるということを利用して,波を周波数ごとに分解する」際に利用するものである(図1)。

余談であるが,「あらゆる波は三角関数の和で表すことができる」に疑問を持った方にはこちらの動画をおすすめしたい。
「YouTube【物理エンジン】円板の組み合わせだけで何でも描けるフーリエ変換の話 Fourier transform」
NIRS データの場合は,脳の応答成分が含まれているかどうかの確認や,フィルタを作成する際に遮断周波数を何 Hz にするのか,作成したフィルタがノイズを適切に減衰させたかどうかなどを確認する際に,その周波数成分を調べる必要がある。
窓関数
前提として,フーリエ変換は連続する(手元にある波と全く同じものが前後に限りなく続く)波に適用するものである。NIRS データは基本的に一定の時間幅で取得されるため,この前提を満たさない。すなわち,得られたデータに対するフーリエ変換は不適切であるということになる。
例えば,以下の場合は360秒–0秒の部分が連続していない(図2)。
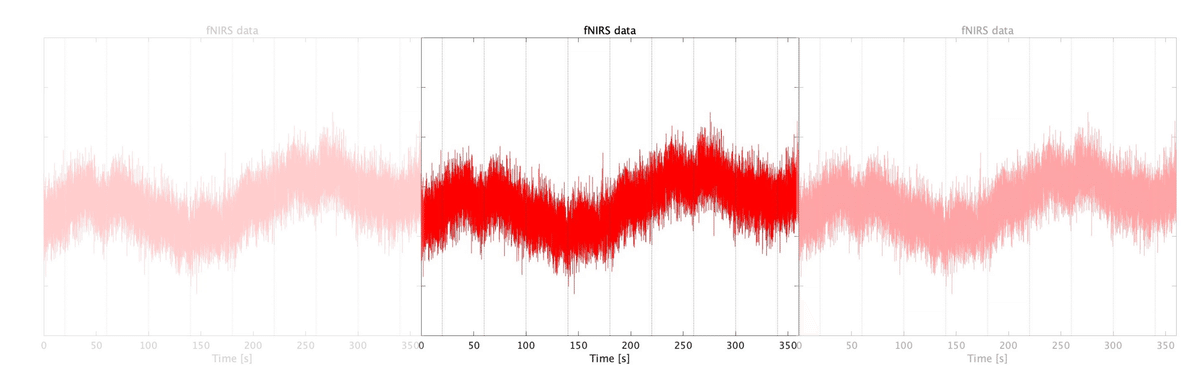
このような不連続性を補正するために「窓関数」というものが使用される。窓関数とは,簡単に言えば,手元の波の両端を 0 にすることで連続するものとみなすために使うものである。
窓関数にも様々なものが存在するが,多くの場合は「ハン窓(ハニング窓)」や「ハミング窓」が使用される。ハン窓,ハニング窓の形状は以下の通りである(図3)。なお,実際にはこの関数を手元のデータに畳み込むため,窓の横幅はサンプルデータに合わせた。

ハン窓は両端を 0 にすることで連続性を確保するが,そのために両端付近に位置する波形の変化(周波数成分の存在)を見落とす危険がある。これを改善するために,連続性を多少犠牲にすることで周波数分解能(周波数の検出性能)を上げたものがハミング窓である。
再び余談ではあるが,MATLAB の関数 "fft" でフーリエ変換をする際に窓関数の設定をしない場合は,矩形窓(全ての時間で 1 となる関数: xy 座標における y = 1 (0 ≦ x ≦ t) の直線)が使用される。この場合の畳み込みは元のデータと 1 との乗算となるため,手元のデータは変化しない。
窓関数による振幅の減衰
フーリエ変換を行う際には窓関数の使用を検討する必要があるが,窓関数を畳み込むと元のデータの振幅が小さくなる(矩形窓は除く)。この振幅の減衰を補正するために,ACF (Amplitude Correction Factor) というものが使用される。
矩形窓の面積を 1 とすると,ハン窓の面積は 0.5,ハミング窓の面積は約 0.54 である(図4)。したがって,ハン窓を使用した場合は変換後の振幅を 2 倍,ハミング窓を使用した場合は変換後の振幅を約 1.85 倍することで,窓関数による振幅の減衰を補正することができる。具体的には,窓の面積の逆数を ACF として,これを変換後のデータに掛ければよい。

窓の有無・振幅補正の有無の比較
サンプルデータ(図2とは異なる)を使用して,元々の波形および窓関数を畳み込んだ場合の波形,並びにそれぞれのフーリエ変換の結果および振幅補正の結果を示す(図5)

補正後の振幅が窓なしと一致していない理由は不明であるが,振幅補正をしない場合の振幅減衰の影響は大きいことがわかる。
まとめ
どんな周波数の波が含まれているのかを調べるためにフーリエ変換を使う。
波の連続性を確保するために窓関数を使う。
窓関数によって振幅が小さくなるのでこれを補正する。
最後に,フーリエ変換についてより厳密な解説をした動画を紹介する。
「YouTube【3Blue1BrownJapan】【視覚的に理解する】フーリエ変換」
