
【内容一部公開】考え方・解き方がスムーズに学べる!――近刊『固体力学入門』
2024年3月中旬発行予定の新刊書籍、『固体力学入門』のご紹介です。
同書の一部を、発行に先駆けて公開します。

***
まえがき
本書は、主として機械工学、航空宇宙工学を専攻し、固体力学を初めて学習する大学学部生を対象として、固体力学の基礎理論をマスターしてもらえることを目指して執筆した。固体力学は機械、航空機、宇宙機、構造などの合理的な設計基準を定める強度解析の基礎工学であり、本書を出発点として固体力学を学ぶことによって、機械構造に対するより精密な構造解析を行うための理論的基盤を得ることができよう。本書の読者としては、力学(可能ならば解析力学)、材料力学をすでに履修済みの読者を想定しており、これらの学問の関連性や、材料力学で学んだ応力やひずみのより詳細な理解が可能になるよう留意して執筆した。
本書は、著者の一人である吉村がもう一人の著者である荒井から2018年以降に引き継いで、名古屋大学の工学部機械・航空宇宙工学科の3年生向けに開講している「固体力学」の講義に基づいて書かれている。
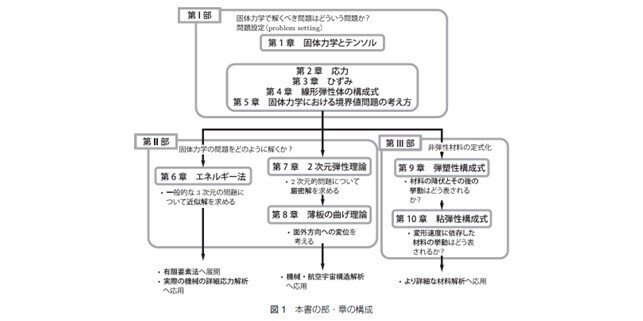
本書は大きく3部から構成されている。まず第I部では、固体力学の基本事項を述べ、固体力学全体の問題設定を理解することを目的としている。第1章では、固体内のひずみや応力の記述に用いられる概念として重要なテンソルを導入する。第2章と第3章では、それぞれ応力とひずみを定義し、それらの性質を述べる。第4章では応力とひずみの関係を記述する構成式について、線形弾性体を対象として詳しく説明した。第5章では固体力学の境界条件について紹介し、固体力学ではどのような問題を解けばよいのか、という全体的な問題設定を整理した。
第II部では、第I部で整理した固体力学の問題についての、さまざまな解き方について記述した。第6章では、エネルギー法について述べる。エネルギー法は現代の機械・構造解析のデファクトスタンダードである有限要素法(FEM)の理論的基礎となるものである。第7章では、問題に幾何学的な制限を加えて単純化し、2次元問題として解く場合について、応力関数を用いた解析法を説明する。第8章では、解析対象を薄板と近似して解く場合の薄板の曲げ理論について記述した。第7、8章は、特に薄板状の構造を扱うことの多い、機械・航空宇宙関連の構造解析には役立つことと思う。
第III部では、応力とひずみの関係が非弾性的な振る舞いを示す場合の材料構成式について導入を行った。第9章では弾塑性理論の基礎を、また、第10章では粘弾性理論の基礎を述べる。
各部、各章の関係については、図1に示すチャートを参照いただくとわかりやすいと思う。なお、第1~8章については吉村が、第9、10章については荒井が主に記述を担当した。
(中略)
本書にはいくつか類書にはないと思われる記述を盛り込んでおり(たとえば第3章、第6章)、記述のこなれていない部分などが入り込んでいるかもしれない。しかし、徒然草第150段にもあるとおり、「なまじいに人に知られじ」として公表しなければ、上達することもない。あえてこの形で世に問い、諸賢のご批判を請いたいと思う。
***
名古屋大学 吉村 彰記(著)
名古屋大学 荒井 政大(著)
【目次】
第I部 固体力学の基本事項
第1章 固体力学とテンソル
1.1 テンソルとは
1.2 2階のテンソルに関する基本的な演算
1.3 総和規約
1.4 座標変換
1.4.1 ベクトルの座標変換
1.4.2 2階テンソルの座標変換
1.5 2階テンソルの不変量
演習問題
第2章 応力
2.1 応力の定義
2.2 コーシーの公式
2.3 応力の不変量
2.4 主応力・最大せん断応力
2.4.1 主応力
2.4.2 最大せん断応力
2.5 平衡方程式
2.5.1 静的問題での平衡方程式
2.5.2 動的問題および体積力がある場合の平衡方程式
2.6 円柱座標系における平衡方程式
演習問題
第3章 ひずみ
3.1 ひずみの定義
3.1.1 変形勾配
3.1.2 ひずみの導出
3.2 ひずみの各成分の意味
3.3 テンソルひずみ・工学ひずみ
3.4 適合条件式
3.5 ひずみの不変量
3.6 主ひずみ・最大せん断ひずみ
3.7 円柱座標系におけるひずみ
演習問題
第4章 線形弾性体の構成式
4.1 一般化フックの法則
4.1.1 テンソルでの表記と成分の対称性
4.1.2 一般化フックの法則の行列表記
4.2 材料の対称性と弾性スティフネス行列の独立成分
4.2.1 材料がある軸に対して2次の対称性をもつ場合
4.2.2 材料が三つの軸に対して2次の対称性をもつ場合(直交異方性)
4.2.3 材料が二つの軸方向に同じ構造をもつ場合
4.2.4 材料がある面内で等方的な場合(横等方性)
4.2.5 材料が等方的な場合(均質等方性)
4.3 弾性定数の表現方法とヤング率,ポアソン比
4.3.1 ラメの定数
4.3.2 ヤング率とポアソン比
4.3.3 横等方性の材料に対する実用弾性定数
演習問題
第5章 固体力学における境界値問題の考え方
5.1 境界条件と固体力学の問題設定の整理
5.2 ナビエの式
第II部 種々の問題へのアプローチ
第6章 エネルギー法
6.1 仮想仕事の原理
6.1.1 固体力学への仮想仕事の原理の導入
6.1.2 発散定理による変形
6.2 ポテンシャルエネルギー最小の定理
6.2.1 ひずみエネルギーの導入
6.2.2 ポテンシャルエネルギー最小の定理
6.3 補仮想仕事の原理
6.4 コンプリメンタリエネルギー最小の定理
6.5 レイリーーリッツ法
6.6 カスティリアノの定理
6.6.1 カスティリアノの第1定理
6.6.2 カスティリアノの第2定理
演習問題
第7章 2次元弾性理論
7.1 平面応力状態
7.2 平面ひずみ状態
7.3 エアリの応力関数
7.4 極座標系におけるエアリの応力関数
7.5 内外圧を受ける円板
7.6 円孔まわりの応力集中演習問題
演習問題
第8章 薄板の曲げ理論
8.1 平板の曲げの基礎式
8.1.1 合応力
8.1.2 平衡方程式
8.1.3 変形とひずみ
8.1.4 構成式(応力ーひずみ関係)
8.1.5 板のたわみ方程式
8.2 正弦波状の圧力を受ける4辺単純支持長方形板
8.3 より複雑な圧力を受ける4辺単純支持長方形板
8.4 極座標系における円板の曲げ方程式
演習問題
第III部 非弾性材料特性
第9章 弾塑性構成式
9.1 弾塑性体の応力とひずみ
9.2 材料の降伏条件と降伏関数
9.3 降伏曲面
9.4 トレスカの降伏条件
9.5 ミーゼスの降伏条件
9.6 相当応力と相当塑性ひずみ
9.7 後続の降伏関数と硬化パラメータ
9.8 塑性ポテンシャル
9.8.1 負荷・中立負荷・除荷
9.8.2 ドラッカーの仮説と最大塑性仕事の原理
9.9 硬化則
9.9.1 等方硬化則
9.9.2 移動硬化則
9.9.3 硬化則のまとめ
演習問題
第10章 粘弾性構成式
10.1 線形粘弾性体の構成式
10.2 粘弾性構成式の温度依存性
10.3 シフトファクターの取り扱い
10.4 フォークトモデルによるクリープ関数の近似
10.5 マクスウェルモデルによる緩和弾性係数の近似
10.6 貯蔵弾性率と損失弾性率
演習問題
付録A ひずみに関する補足
A.1 連続体力学における微小ひずみの導入
A.2 本文中の説明と連続体力学による定義との関係
付録B 質点系における仮想仕事の原理・補仮想仕事の原理の証明
B.1 仮想仕事の原理
B.2 補仮想仕事の原理
付録C 解の唯一性の証明
演習問題略解
参考文献
索引
