
組み立てパズル愛 ー八十路個人事業主の製品開発ー
まえがき
亡父が認知症を発症した年齢になったので中高年層の認知症予防と小学生の孫たちを含む年少者の知育を兼ねた新しい組み立てパズルを開発出来ないかと考えた。
パズルショップ[トリト]さんのホームページで知った小田原さんの[箱詰めパズル天国]を覗いてみると、箱詰めパズルの基礎や応用、開発例が盛り沢山に記載されていた。
また、そこで紹介されていた石野さんの[ちょいとパズルでも]を開いてみたら、世界中の作家の作品がまるで辞典のように大量にリストアップされていて、とても箱詰めパズルには参入できそうになかった。
しかし、ユニーク解(一つだけの答)の追求など、パズルとして、より難解な方向へ向かっている感じがしたので、まず、初心者や年少者、高齢者などが取り組みやすい組み立てパズルの開発を目指すことにした。
第1章 新しいキューブパズルの組み立て方法
1、キャビティキューブパズルの開発
実際に知育玩具として知られている3×3×3ユニット(以後、3Xと略す)のソーマキューブを試作して、ショップに来られたお客さんにトライしてもらうと、初めて箱詰めパズルをする方のほとんどは短時間であきらめてしまわれる。
また、4×4×4ユニット(以後、4Xと略す)のキューブより大きいユニットのパズルはピースの数も増えて組み立てがより難しくなる。
箱詰めパズルの世界に入り込む余地が無ければ隙間をつくるしかないので(?)、空洞(Cavity)をつくることにした。
新発想の箱形の箱詰めパズルである、キャビティキューブ パズル(Cavity cube puzzle)の誕生である。
キャビティキューブパズルとは、n×n×nユニット(nX)の6面体の内部に(n-2)×(n-2)×((n-2)ユニット相当のキャビティを有するキューブを複数個のピース(ポリキューブ)で組み立てるパズルである。
【ピースを構成するポリキューブとは1ユニットのモノキューブの面と面を接着して複数個つないだもので、n個のユニットのポリキューブをn―キューブと呼ぶ。平面型のポリキューブはプレイナーポリキューブと呼んで3次元ポリキューブと区別されるのだが、筆者が使うのはほとんど平面型なので単にポリキューブと呼ぶ。】
キャビティキューブの特徴は、まず6つの面を壁のように組立てるので、取り組みやすいことと空洞分のユニット数を少なくできることなどである。
また、マトリョウシカのように例えば7Xのキャビティキューブには5Xのキャビティキューブを、5Xのキューブのキャビティには3Xのキューブを入れ子(中子)にできる。
1)、4Xキャビティキューブの試作
最初の試作品である4Xのキャビティキューブは、9-キューブ4個、10-キューブ2個の合計6個の形状の異なるピースの組合せである。

2)、5Xキャビティキューブの試作
この試作品は5Xのキャビティキューブである。ピースはすべて形状の異なる6個のピース(ポリキューブ)で、ピースの中央に1ユニット分の窓を開けている(任意)。

次の例は5Xのキャビティキューブで、ピースは12個のポリキューブだが、まず、各2個ずつの凸凹をはめ合わせて1つの面としてから、ボックス状に組み立てる。はめ合わせるピースの組み合わせが様々なので難度は少し高くなる。

3)、7Xキャビティキューブパズル
20mm角のローズウッド343個(ユニット)で、7X(24ピース)と5X(12ピース)と3X(6ピース)のキャビティキューブがマトリョウシカキューブとして完成した(モノキューブで3Xのキャビティを埋めてもよい)。
組み立てパズルとしては超難問に見えるが、3Xキューブから5Xキューブへと順々に組み立てていくと、従来の7Xのソリッドキューブほどは難しくない。
各キューブのピースの色や材質を変えるとさらに易しくなる。


このように、キャビティキューブパズルは、従来の、ソリッドキューブをやみくもに積み上げるイメージのパズルが、各面を組み立てた後ボックス状に組み上げる新しい概念の組み立てキューブパズル(箱形箱詰めパズル)となった。
このパズルは初心者でも取りつきやすく、年少者の知育や年長者の脳トレなどにも活用できるし、パズル愛好家に満足してもらえる難度にもできる。
また、ユニットキューブの総数が少なくなるため、より大きな立体パズルに取り組みやすくなる。
これらは特許出願済で、公開されている。
2、シンメトリーキャビティパズル
1)、5Xシンメトリーキャビティパズル
形状の異なる全てのピースが裏返しても同じ形になる線対称形のピースで5Xと3Xのキャビティキューブを組み立てる。
3Xはモノキューブ(サイコロ)を中央においても、外して空洞にしてもよい。


2)、5Xシンメトリーカラーボックス
まず、線対称形の12ピースを2個ずつ組み合わせて、形状の異なる6個の線対称形セットにする。
それで、内部に3X相当のキャビティをもつ5Xのボックスを組み立てて下さい。
線対称形は裏返しても同じ形で裏面の色が異なるので、組立て後に面の色を変えることができる。


3)、シンメトリー貯金箱パズル
6個の形状の異なるシンメトリーピースで5Xのコインボックスができた。家内は500円硬貨の貯金に使っている。

3、Diagonal Symmetry(対角線対称形) Box puzzle
1)、対角線対称形とは
正方形は2本の垂直二等分線と2本の対角線を軸とした線対称形だが、立 方体が面どうしでくっついた平面型ポリキューブでも線対称形(ひっくり返しても同じ形になる)を作れる。
数学など少し調べてみたが、線対称形をさらに細分化した名称が見つからなかったので、対角線対称[Diagonal (Line)Symmetry] は筆者の造語である。
前項までのシンメトリーキャビティキューブでは主に垂直線対称形の例を紹介したが、ここでは対角線軸を有するすべて形状の異なる線対称形のポリキューブで組み立てたDiagonal Symmetry Box Puzzleを紹介する。
2)、4X対角線対称ボックスパズル
美しい対角線対称形に出会って初めての4Xボックスの試作品は2種類のピースの組み合わせと3種類のピースの組み合わせだった。
最初に2種類の方の組み合わせが見つかった時は筆者にとっては大発見?で、うれしくて眠れなかった。


3種類の組み合わせから、形状の異なる6個のピースを探すのに1か月以上かかり、一旦あきらめたが、5Xで何とか見つかったので再挑戦してやっと完成した。

3)、5X対角線対称コインボックスパズル
BCP(Bill Cutler Program)のようなソフトを持たないので、試行錯誤で1か月近く費やしてすべて形状の異なる6個の対角線対称ピースを見い出し、5Xの対角線対称コインボックスが完成した。
裏面を異なる色で彩色すると裏側にひっくり返しても同じ形なので全面同じ色で統一することも出来る。

さらに、6個のピースを各々2つに分割して、12個の形状の異なる対角線対称のピースの組み合わせを発見した。


4)、 Diagonal Symmetry Box puzzle(対角線対称ボックスパズル;以下DSパズルと略す)6Xと7Xを紹介する。
今回は机上(パソコン)で、展開図からの開発を試みた。
(1)、6X DSパズル
解が沢山あるので全て形状の異なるピースの一例を示す。

各ピースを2分割しても全て形状の異なるDS(対角線対称) ピースを凹凸嵌合出来るようにした。

(2)、7X DSパズル
これも解が沢山あるので全て形状の異なるピースの一例を示す。

一つの面を4分割すると全て形状の異なるDSピースは不可能なので、6種類のDSピースにした。
ヒント:・各ピースの表と裏の色は異なる。
・各面を構成するピースは6色のうち、同一色である。
・6種類の形状の裏面の色は同一形状のピースは同じ色である。

ここで終わらないのが筆者の真骨頂(?)で、4分割のピースが24個なので、4X(4×4×4ユニット)のDSボックスを4個組み立てられそうだ。
ユニット数を計算してみると、残念ながら(4X)×4では224ユニット必要なのに、(7X)は218ユニットで6ユニット不足している。
しかし、4Xの8つのコーナーは欠けてもボックスは成り立つ(?)ので、7Xのピースの形状から見直して見事に4個の4X対角線対称ボックスが完成した。
欠けたコーナーはユニットがあってもなくてもピースの対角線対称形が成立している!神業か?

(3)、7X DSボックス+5X DSボックス+3X DSボックス
対角線対称形のピースによる3Xボックスを5Xボックスのキャビティに入れ子にし、この5Xボックスを7Xボックスのキャビティに入れ子に出来た。
7Xボックスを構成するピースを24個にすれば5Xボックスのピースと類似するため、彩色を同じにすればパズルとしては面白くなる。

第2章 3種類のキューブパズル組み立て方法
1、スライスキューブの考案
先のキャビティキューブパズルに続き、[スライスキューブパズル]を紹介する。
従来の箱詰めパズル(組み立てキューブパズル)は闇雲に積み上げると、初心者には取りつきにくい一面があった。
そこで、まず各面(壁)を作った後、組み立てるキャビティキューブパズル(Cavity Cube Puzzle)を考案したが、さらに初心者でも取り組みやすいスライスキューブパズル(Slice Cube Puzzle)の考案に至った。
スライスキューブパズルとは平面型ポリキューブだけのすべて形状の異なるピースで組み立てるキューブを、まず、各段層にスライスした平面をジクソーパズルのように組み立てた後、積み上げてキューブとするパズルである。
なお、従来のキューブパズルのように、ピースを縦方向にすることも含めて積み上げることも可能とした。このように、縦、横の段層を少なくとも一つのピースが横切る従来の組み立てキューブをランダムキューブと呼ぶことにする。
1)、5-C以下1-Cまでのすべて形状の異なるポリキューブからなる16個のピースをセレクトした。

① すべてのピースを使って4x4x1ユニットの平板を4枚組み立てる(スライスキューブ)。

② すべてのピースを使って4Xのランダムキューブを組み立てる(各断層はスライスできない)。
(写真は省略する。)
③ 任意のピースを使って3x3x1ユニットの平板を3枚組み立てて3Xスライスキューブを組み立てる。

④ 直方体のピースを使わないで3Xのランダムキューブを組み立てる。
(写真は省略する。)
2)、6-C以下1-Cまでの形状の異なるポリキューブからなる42ピースをセレクトした。
一見、難しそうだが、難しかったのはピースのセレクトで、苦労させられたが、スライスキューブを組み立てるのはそうでもない。
このセレクションでランダムキューブも可能なので、その違いを想像してほしい。

① すべてのピースを使って6x6x1ユニットの平板を6枚組み立てる。

② すべてのピースを使って6Xランダムキューブを組み立てる。

2、3種類すべて組み立て可能なピースセレクション
1)、スライス、キャビティ、ランダム3種類の組み立て方がそろったので、この3種類(ゴールデントリオと呼ぶ)とも組立て可能なセレクションを紹介する。
3Xのセレクションは1-C 1個、2―C 1個、3-C 2個、4-C 2個 、5-C 2個の8個(27ユニット)。
なお、3×3ユニットの大きさ以内のピースは4-Cが4個、5-Cが6個あるが、4-Cと5-Cの組合せで3×3×1のスライス板が3組できるので、そのうち2組を選ぶ。

2)、1―Cから5―Cまでの18ピース(74ユニット)を使って、4Xのゴールデントリオ(ランダム、スライス、キャビティ )を組み立てて下さい(余り10ユニット)。キャビティキューブは入れ子の2Xを含む。

3)、2-Cから6-Cまで、3×3ユニットの大きさ以内のピースは20個あります。
この中から合計(27+26+27)ユニットのスライス、キャビティ、ランダムキューブを組み立てる(キャビティの1-Cは除く)。

3、6方向カラーキューブパズル
ピースの数が多くなると、ゴールデントリオのうち、ランダムキューブを組み立てる時の取り掛かりが難しくなる。
そこで、キューブ外面に特定のマークを付ければ、ユニーク(単一)解となるが、取り掛かりやすく解のヒントにもなる。
1)、外表面着色
まず、思いついたのは任意の面数に線又は色を付けることであった。

2 )、6方向識別カラーキューブ
着色の場合、各ピースの面の色を同じ方向の外面の色と合わせたら、外表面だけよりより少し複雑となるが各ピースがきれいになり、解のヒントになる。これは新しい発想である。
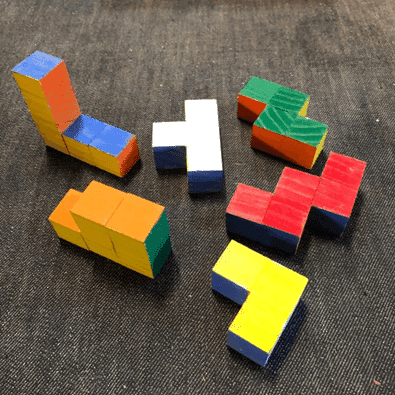
3)、カラーマーク
着色の代わりや着色と併用して、カラーマークにしてもよい。

4)、Mori's Color Cube Puzzle
これは[Rubick's Cube]ではない。[Mori's Color Cube Puzzle] である。
4Xキューブで、前項で紹介したゴールデントリオ(スライス、キャビティ、ランダム)キューブのデモ用モデルだが、ランダムキューブを6方向識別カラーピースにしている。

ランダムの方は解の数が多いので、キャビティの方を6方向識別カラーとしてもよい。

5)、5Xマルチカラーキューブパズル
5-C以下1-Cまでの形状の異なるすべての平面型キューブと長辺が3ユニット以下の6-Cの27ピースをセレクトし、各ピースの6つの方向面に6種類のカラーを配した。
【Multi Color Cube Puzzle(5X―-1)】

① 1-C以外のすべてのポリキューブピースを使って、3X(1ホール)と5X(3X相当ホール)キャビティキューブを同時に組み立てる。ヒントは各外面が同一のカラーとなることです。

② カラーを無視し、すべてのピースを使って5Xランダムキューブを組み立てる(写真は省略)。
③ カラーを無視し、すべてのピースを使って5x5x1のスライスを5枚組み立てる)。

④ カラーを無視し、直線状の5-Cだけを除いたピースをすべて使って4Xキャビティキューブ(2X相当ホール)と4Xランダムキューブを同時に組み立てる。

【 Multi Color Cube Puzzle (5X-―2)】
6—Cの1個を取り替えたが、①、②、③、④ はクリアーした。
下の写真は② 5Xランダムキューブである。

⑤ カラーを無視し、適当なピースを選んで3Xキューブを3セット同時に組み立てる。
ランダムキューブ1セットとスライスキューブ2セットである。
(ランダムキューブ3セットにもできる)。

⑥ カラー無視で任意のピースを選び、3Xと4Xのスライスキューブを組み立てる。

⑦ カラー無視で次の平面を埋める。
12×10ユニット(5ユニット余る)と、11×11ユニット(4ユニット余る)。

本章のスライスキューブなどは特許出願済で、公開している。
第3章 数式キューブとの出会い
1、3 cube + 4 cube +5 cube = 6 cube
cube が立方体の意味ならこの等式は成り立たないが、複数(cubes)ではないのでおわかりのようにcubeには立方、三乗の意味がある。
(3の3乗)+(4の3乗)+(5の3乗)=(6の3乗)の数式を英訳すると表題になる不思議さ。つまり、Cube Puzzle で具現出来ることを暗示しているようだ。
数学において(aの2乗)+(bの2乗)=(cの2乗)はピタゴラスの定理で知られているが、(aの3乗)+(bの3乗)=(cの3乗) はフェルマーの最終定理によって、この式の a、b、c の自然数解は存在しない。この定理はフェルマーの死後330年にわたって証明を試されてきたが、1995年にワイルスによって完全に証明されたそうだ。
ところが、(aの3乗)+(bの3乗)+(cの3乗)=(dの3乗)の a、b、c、dの自然数解は一桁の自然数の中に連続して存在したのだ。
(3の3乗)+(4の3乗)+(5の3乗)=(6の3乗)の数式をキューブパズルにした、6Xのキューブの構成ピースを使って3Xと4Xと5X のキューブを組み立てる。
これを1961年に最初に公表したのがWhieeler であるとブログ[Puzzle of MINE]で植松氏が紹介されている。
しかし、8ピースで3Xのキューブはそのままだったそうで、氏自身も2008年に直方体を含まない8ピースを考案されているが、パズルとしてはピースの数が少ない。
本格的なパズルはこれより前(2000年)に春秋工舎(有)の荻野氏の特許がある。特許3078263号
これは35種類の6-C(キューブ)から直線状の1個(5Xで使用できない)だけを外し、代わりに直線状の3-C、4-C、5-Cを追加して数を合わせた37個のピースであって、特許にふさわしい感動的な発明である。
そこで、筆者も6-C以下の大きさで、直線状など直方体を含まない組合せや3-Cの3次元形状を含む、よりピースの数の多い組合せに挑戦してみることにした。
【追記】
本稿の「あとがき」記述の参考にしたくて、組み木作家小黒三郎氏のエッセィ[組み木の夢]を読んでいたら[1981年、北海道立近代美術館主催の「第1回はこでかんがえるー遊びの木箱」に「動物の箱・四つの立方体」を出品。45匹の動物ポリキューブで四つの立方体に組むことができ、3^3+4^3+5^3=6^3という数式がヒントになって生まれた](121page)とありました。この作品は現在、島根県益田市匹見町のウッドパークの世界のパズルを集めたパズル館に展示されているそうだ。いつの日にか訪れて45のポリキューブのセレクトを確かめてみたい。今のところ筆者の中ではこれが日本で一番古い数式の応用になります。
1)、試作品(その1)
6―C以下の大きさのすべて形状の異なる平面型ポリキューブに限定。ただし、線形など直方体の形状は除外する。また、数合わせの関係で5-C 2個と6-C 7個も除外した。
使用ピースは以下の39個である。
3-C 1
4-C 3
5-C 9
6―C 26
内訳は
3X;4-C 1、5-C 1 6-C 3
4X;3-C 1、4-C 1 5-C 3、6-C 7
5X;4-C 1、5-C 5 6-C 16

2)、試作品(その2)
3ーC以上、6-C以下の大きさの形状の異なるポリキューブに限定。
直線状、直方体、3次元形状を含む。
使用ピースは以下の44個である。
3-C 2
4-C 8
5-C 26
6-C 8
内訳は
3X;3-C 2、4-C 1、5-C 1、6-C 2
4X;4-C 7、5-C 6、6-C 1
5X;5-C 19、6-C 5
3)、試作品(その3)
6-C以下の大きさのすべて形状の異なる平面型ポリ(モノ)キューブに限定。線形など直方体の形状も含む。
使用ピースは以下の42個である。
1―C 1
2-C 1
3-C 2
4-C 5
5-C 11
6-C 22
内訳は
3X;4-C 1、5-C 1、6-C 3
4X;3-C 1、4-C 1、5-C 3、6-C 7
5X;1-C 1、2-C 1、3-C 1、4-C 3、5-C 7、
6-C 12
2、数式キューブをゴールデントリオで挑戦
前章のスライスキューブの開発で紹介した、6-C 以下1=C までの42ピースのセレクションをベースに、3Xと4Xと5Xのスライスキューブを同時に組み立てることに挑戦した。
しかし、2か月以上悪戦苦闘したがどうしても解決できない。
これまでも、キャビティキューブの対角線対称ピースなど、あるかないかわからないものをあると信じて、試行錯誤して見つけ出してきたが、今回はこれだけ時間をかけてもダメなので、無理だと感じた。
仕方なく、封印してきた最後の手段を使うことにした。7-Cの投入だ。
6-C 3ピースと5-C 2ピースを7-C 4ピースに変更した。
1)、6X=3X+4X+5X ゴールデントリオ
7-C以下の大きさのすべて形状の異なる平面型ポリ(モノ)キューブ(線形など直方体の形状も含む)。
6X使用ピースは以下の41個である。
1―C 1
2-C 1
3-C 2
4-C 5
5-C 9
6-C 19
7-C 4
(3X、4X、5Xの内訳は省略する。)
① 6Xのゴールデントリオ
ランダムキューブ(RC)は6方向カラー識別している。
キャビティキューブ(CC)は入れ子まで組み立てる。

② 3X+4X+5Xのゴールデントリオ
ランダムキューブの4Xと5Xは6方向カラーシールで識別している。
キャビティキューブの3Xと4Xの入れ子は1-Cが欠かせないが、5Xで使っているので、入れ子なしとなる。

③ (おまけ)4Xのゴールデントリオ

④ (おまけ) 3Xのゴールデントリオ+5Xランダムキューブ
(3Xのゴールデントリオ+5Xスライスキューブは省略)

⑤ (おまけ)5Xキャビティキューブ 2セット
(余りのピースはキャビティに収納できる。)

以上、思い描いた通りの究極とも思える数式キューブのゴールデントリオが完成した。
第4章 究極の組み立てキューブパズルを求めて
1、マルチ組立てキューブ Multi Assembled Cube
従来の箱詰めパズル(組み立てキューブパズル)はピースをやみくもに積み上げるイメージであったため、初心者には取り組みにくいパズルであった。
そこで、ピースをすべて形状の異なる平面型に限定し、前章まででゴールデントリオと称した3つの組立て方法を確立した。
① キューブの各段層でスライスした平板を組み立てた後。重ね合わせるスライスキューブ
② 内部に(n-2)の2乗の空洞を持つキューブを、シンメトリーボックスなどは6つの面を組み合わせるが、ピースの数が多くなると底面と4つの側面と上面の順に組み立てるキャビティキューブ(可能なら空洞を埋める入れ子のキューブを含む)
③ 縦横の段層で平面に分離できないように組み立てるランダムキューブ
以上の3つの方法で組み立てるキューブを、商品化を控えて、今後MAC(Multi Assembled Cube)と呼ぶことにする。
2、改良数式MAC
前章の数式ゴールデントリオでは各ランダムキューブを6方向カラー識別で補助したが、初心に帰って考えてみると、6Xの41個のピースから3Xと4Xと5Xのピースを選んで、同時に3つのキューブを組み立てるのは初心者にとっては難しすぎた。
そこで、逆転の発想で、6X用のピースを3X用と4X用と5X用に分けて、易しい3Xから順番に各MACを組み立て、その後に全ピースで6XのMACを組み立てる案を考えた。
さっそく、スライスキューブの3X、4X、5Xのピース郡を木材の色を変えて検証した.
結果はキャビティキューブの4Xと5Xだけが分離できず、各ピース郡を一から見直さなければならなくなった。最後の難関である。

3、究極のMAC
1)、初心者向けの分離
少し時間がかかったが、3X、4X、5Xを各々分離してMACを組み立てることができるピースの再配分に成功した。
初心者向けの3X用と4X用ピースを分離し、上達者向けに5X用を追加することにした。
初心者向けのピースにはNo.1からNo.20まで番号をしるした。
(番号の代わりに3Xと4Xのピースの木材の色を違えてもよい)。


【入門コース】
第1ステージ
No.1からNo.7ピースを用いて3XのMACを組み立てる。
(ランダムとスライスの写真は省略)

第2ステージ
No.8からNo.20ピースを用いて4XのMACを組み立てる。
(ランダムとスライスの写真は省略)

【ファイナルコース】
第3ステージ
21個のピースを用いて5XのMACを組み立てる。
(ランダムとスライスの写真は省略)

第4ステージ
41個すべてのピースで6XのMACを組み立てる。
6Xラ ンダムキューブは6方向カラー識別の例だが、カラーを無視し
ても多くの解がある。)

ファイナルステージ
すべてのピースを使って、
① 3XのMACを同時に実施、余ったピースで5XのMACを組み立てる。
② 4XのMACを同時に実施する。
③ 5Xのキャビティキューブを2セット組み立てる。余りのピースをキャビティに収納する。
以上の3点は前章の数式ゴールデントリオで紹介したので写真は省略する。
ファイナルファンタジー
数字やカラーを無視してすべてのピースを使って、オリジナルの3X+4X+5XのMACを組み立ててください。

第5章 転がしても崩れないダイスパズル
1、3X 組み木ダイスパズル
1)、ダイスパズルとの出会い
2018年のSOMA NewsにTheo's spotted cubesの一つとしてdice SOMA cubeが紹介されていた。240ほどある解をユニーク(単一)解にする手段である。しかし、7個のSOMAピースではダイスとして転がしたら崩れてしまう。
そこで、転がしてもくずれないダイスパズルを開発することにした。
はじめは、寸法精度を上げて凹凸の嵌合を中心に試作したが、時間がたつと木材の収縮で緩んでしまい、何回も転がしたら崩れてしまった。
しかし、組立てパズルとしては、ダイスの特徴である「サイの目とそれを反対面と合わせた数は7である」ことは、組み立てる時の大きなヒントになる。

また、塗装することでもこの問題は解決できた。全面塗装で、色の濃いユニットをサイの目とした[3Xカラーダイスパズル]である。 しかし、塗装しない場合は3次元ピースを主にした組み木技法を習得する必要がある。

2)、新製品[3X組み木ダイスパズル]
3次元ピースを主とした開発に当たってはピースのユニット数のユニークさにこだわった。断らない限り、すべて形状の異なるピースの組み合わせである。

① トリプル9 3Xダイスパズル

② トリプル8+3 3Xダイスパズル

③ トリプル7プラス6 3Xダイスパズル

④ トリプル7プラス5 3Xダイスパズル(1ホール)

⑤ ダブル10プラス7、ツイン11(同形)プラス5、ツイン12(同形)プラス3、鏡面対称形13 3Xダイスパズル

⑥ シリアル5678、シリアル8、9、10(2セット)、ワンジャンプ7、9、11(2セット)3Xダイスパズル

⑦ 中心棒シリーズ
・ クアドラプル6プラス3、シリアル789プラス3、トリプル8プラス3、ツイン12 3Xダイスパズル

・ ワンジャンプ6、8、10プラス3(2セット) 3Xダイスパズル

3)3セットのピースをごちゃ混ぜにして3個のダイスを組み立てる難問?
① ラッキー777プラス6 3セット(その1)

② ラッキー777プラス6 3セット(その2)
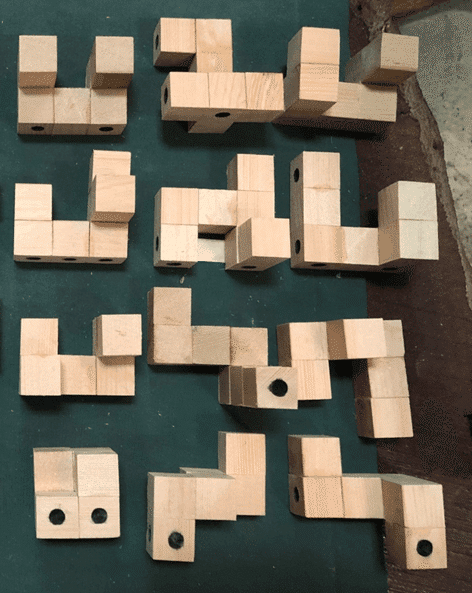
③ トリプル9 任意の3セットまたは5セット

④ (参考) ラッキー777プラスα (①、②を含む10セット)
赤、白、青、緑、黄のシールが同じ形なので、33種類のピースで10セットを組み立てている。

2、4X組み木ダイスパズル
1)Coffin氏作品のモデファイ
4Xキューブのダイスパズルは各サイの目が分割されるため、解のヒントとしては分かり易くなる。
開発に当たってはパズルコレクターの[たに~]氏にTwitterで紹介してもらったCoffin氏のInterlocking Cube[Convolution]をヒントに、9~10ユニットの7ピースを8ユニットの8ピースにモデファイすることにした。名称由来の回転ピースは敬意を表して使わないことにしたが、完成するまでに実働でほぼ1か月を要した。あたり前だが、Cofin作品と同一形状のピースは一つもなく、組立て最終の貫通ピースを内側に移動できたので、スマートな改良新製品になったと自負している。

2)、オリジナル4X組み木ダイスパズル
先に紹介した新製品[4X組み木ダイスパズル]は開発に当たってCoffin氏の7ピース(9ユニット6個+10ユニット1個)をヒントに8ユニットの8ピースにモデファイしたと述べたが、石野恵一郎氏の「ちょいとパズルでも」のリストを調べてみると、1991年に柳瀬順一氏が4種類の8ユニット8ピースのInterlocking Cubeを開発されていた。これらがすごいのは30個の異なる形状で4セットをつくられている、つまり、#3だけが2個ダブっているだけなのである。
先の筆者の作品はすべてのピースが30種類とは異なる形状であったが、予想していた通り、組み木としては筆者のレベルが低いのが幸いしていたようだ。
今回、第2弾として発表する同じく8ユニット、8ピースの4Xダイスパズルについては、柳瀬氏の#2と3ピースが同一形状であったが、5ピースが30種以外の新形状であった。
#2は組立時に3か所Moveが必要だが、私は「出来るだけ易しく」したいのでNo Moveとしている。
また、ダイスパズルなので分割されたサイの目を合わせれば、組み立てがより易しくなる。
サイの目は手作りのゴム印で、インクはシャチハタTATである。
市販の場合はドリル穴やレーザー加工に変更してもよい。

本章の組み木ダイスパズルは特許出願しないで公開するが、著作権は留保する。
第6章 さらに新しい組み立てキューブを求めて
1,ハーフキューブパズル
1)、ハーフキューブユニットピースパズル
ゲーム用駒の材料のハーフキューブ片がたくさん残っているので、このハーフキューブユニットでピースを作って、組み立てキューブパズルにするアイデアがひらめいた。
30×30×15(mm)のハーフキューブユニット3枚を、のり代30×15(mm)以上で接着した、すべて形状の異なる18種類のピースを組み立てて90×90×90(mm)のキューブ(15mm角で6×6×6相当)にするパズルである。
形状の異なるピースを次々に試作しているうちに、側面の形状が6-オミノ(平面形ポリキューブ)があることに気が付いた。さっそくハーフキューブで作成可能な側面が6-オミノ形状のピースを調べたら 35種類中23種類あった。
まず、山カンで平板状の1点と難しそうな形状の4点を除外(プール)した。

平面状に積み上げるのを主体に組み立て始めてみたが、無茶苦茶にむずかしくて、すぐには出来そうになかった(30mm幅に限定したのがかえって悪かった?)。
こんな時、BCPソフトがあればすぐに解がわかるのだろうが、筆者は得意のKKD(経験と勘と、度胸より努力)で時間をかけて組み立てるしかなく、明日から頑張ろうとかたずけ始めたら 奇跡 が起こった。
側面を上にした6-オミノ形状を適当に組み合わせながら集めていたら、90×90(mm)の一段目ができてしまったのだ。筆者が先に開発したスライス組み立て法である。あと2段も簡単にできて、パズルが完成した。

筆者の山勘セレクトが奇跡を生んだのか、ほかのセレクトでも可能なのかは分からない。また、ランダム積み上げでも解があるのかも分からない。
いつかゆっくり確認してみよう。
2)、6-オミノツインピースで6^3=3^3+4^3+5^3
ハーフキューブパズルで解が見つかったので、同じセレクションの6-オミノピースを2個ずつにすれば、スライスキューブの解はわかっている。
このセレクションで、先述の[第3章 数式キューブとの出会い]の3の3乗(3X)+4の3乗(4X)+5の3乗(5X)=6の3乗(6X)にトライしてみることにした。
ただし、すべてのピースが6ユニットだから、3Xは27ユニットなので3ユニットが、4Xも同様に64ユニットなので4ユニットが、5Xも125ユニット必要なので5ユニットが必要になる。
そのため、任意の一つの6-オミノを3ーオミノ2個に、もう1つの6ーオミノを2-オミノと4ーオミノに分割する。。そうすると5ユニットは2-オミノ+3ーオミノになる(ナイスアイデア!)。

まず、3Xの組み立てはL型の3ユニットピースと6-オミノ4ピースで完成。
次に、4Xは直線型の4ユニットを使って何とか完成したが、5Xがなかなか解けないので、最終的にはL型の4ユニットピースと6-オミノ10ピースに変更した。
5Xは2ユニットピースと直線型3ユニットピースを使えるのだが、無茶苦茶に難しくて4Xとピースの交換をしたり、分割する6-オミノを変えたりで、完成までに実働40時間以上かかってしまった。
今までも1か月以上かかった時もあったが、筆者の座右の銘【苦しさのなおこの上に積もれかし限りある身の力試さん】のおかげで解決してきた。


【付録】座右の銘
座右の銘といえば、一般に自分で選んだり、作った言葉が多いようだが、筆者の場合は元服?を機に親父から与えられたものである。
名門高校に進学したいので中学3年から母方の伯父の家に寄宿することになった。そのときに、親父から愛用のパーカー万年筆と真新しい手帳をもらった。その手帳の見開きに達筆で、山中鹿之助由来の前述の和歌が記されていた。
以来、66年間、プライベートや仕事の上で大きな難問にぶつかっても、むしろ楽しんで乗り越えてこられたありがたい座右の銘である。
(3)、6オミノツインピースで6XのMAC に挑戦
調子に乗って、先述の[第4章の1、マルチ組立てキューブ(MAC)] にも挑戦してみることにした。
①のスライスキューブはすでに解決している。

②のランダムキューブは分割したピースを別々に使用することで2日がかりで何とか解決した。

③のキャビティキューブでまたしても 奇跡 がおきた。
6Xキャビティの組み立ても分割したピースを別々に使うのだが、苦労して完成することができた。
これでMAC完成にしようと思っていたのだが、残りのピースを調べてみると、すべてが4ユニット長以下で、4ユニットの分割ピースも残っていた。
がぜん、その気になって4Xの入れ子を組み立ててみると、見事に完成した。2度も起きたら 奇跡 とは言えない? 神業?

2,Mirror symmetry pieces of harf-cube units
(ハーフキューブ片による鏡面対称形ピースセット)
前の「1、ハーフキューブユニットピースパズル」では側面の形状が6-オミノ(平面形ポリキューブ)を23種紹介したが、今回はそれ以外の30×30×15(mm)のハーフキューブユニット3枚を、1ユニット当たりのノリ代30×15(mm)相当以上で接着した、すべて形状の異なるピースを紹介する。
その前に、先に紹介した側面が6-オミノ形状の23種類には対応する鏡面対称形のピースは存在しない。側面を上にした鏡像は平面図と同じようにひっくり返したら同じ形になってしまうからである。
これらと同じように下の写真の6点は対応する鏡面対称は存在しない。ピースの形状が線対称形なので、垂直線対称形が180度、対角線対称形は90度回転させれば同一形状になってしまうからである。

今回の筆者の目論見はすべて形状の異なる鏡面対称のピースを9ペア(18ピース)を選び、90×90×90(mm)のキューブ(15mm角で6×6×6相当)に組み立てるパズルを創作することである。
まず、平面状において高さが30(mm)以下の鏡面対称ピースペアを15組選別した。

この中から時間をかけて9ペアを何回も選びなおしたが、今回は奇跡が起きず、あきらめてすべての鏡面対称ピースペアを追加することにした。
追加のペアは下の写真の9ペアで、合計24ペア(48ピース)になった。

24ペアから異なる9ペアを勘ピューターで選んで10日以上試行錯誤したが、箸にも棒にもかからなかった。
すべてを選んで試すことはコンピュータ以外には考えられないので、今回はあきらめることにした。
鏡面対称ペアをあきらめて鏡面対称ペアを持たない6点を加えた合計50個のピースから18個を選べば、時間はかかったがキューブは何とか組み立てることはできた。
しかし、目論見のミラーシンメトリーピースペアではないので意味がない。

3、すべて形状の異なる対角線対称Half-cube ピースによるCoin box パズル
先に投稿したDiagonal Symmetric Coin Box Puzzleで紹介した5×5×5ユニットBoxを、Cubeの代わりにHalf-cube を使えば資材を節約して軽量化できる。

1)、ハーフハーフキューブの追加
しかし嵌合部がはみ出して機能的ではないので、嵌合部をhalf half-cube に変更し、コーナー部をquarter Half-cubeに変更したらスッキリした。
新製品「対角線対称タイルによるコインボックスパズル」の誕生である。

コイン投入面はひっくり返すとコインが取り出しにくくなる。

2)、奇跡のあっと驚くびっくり箱(キューブ)
新製品が誕生したがこれだけでは終わらないのがパズル愛(?)である。
この製品は一つの面(ピース)に3×3ユニットのHalf-cube を使っているが、これを2×2にすると先に開発した4×4×4cube box の対角線対称ピースのパターンが使える。

さらに、1つの面に1つのHalf-cube にしたらどうなるか。
嵌合部のユニットがすべてquarter Half-cube(mini cube)になり、2×2Half-cubeと同じ4×4×4 cube boxの対角線対称ピースのパターンが使える。

これでおしまいにするつもりだったが、3種類のBox puzzleを並べてみると各キャビティにピッタリ収まるマトリョーシカ(入れ子)になっている。

Coin boxにコインが入らないので上面のピースを開けてみると中は2つの入れ子とサイコロでびっしり詰まった奇跡のびっくり箱(キューブ)になっているのである。

【付録】今回の試作で使用したHalf-cubeはマルゴ/マルゴニアゲーム(マルチ五目並べ)用ブビンガ駒の残り材料であった。
コイン投入口に使用しているのが木口のきれいなブビンガ木材である。

4、ハーフキューブユニットがなくなった
前項の2)、奇跡のあっと驚くびっくり(貯金)箱のその後の展開である。
貯金箱をやめて、パズルに特化した省資源策として各面のピースを嵌合部と連結する部分以外を除去して窓を開けたらハーフキューブがなくなった。
1)、8×8×8ユニットミニキューブ
キューブの外形で見ると、当初の5×5×5キューブユニットが、ハーフキューブユニットで余分のはみだしを除いて4×4×4キューブユニット相当となり、現在は当初のキューブの1辺の長さ(30mm)が2分の1(15mm)のミニキューブで8×8×8ユニットになったのだ。
6つの面のすべて形状の異なる対角線対称形のピースの組み合わせパターンは5×5×5ユニットのままであるが、8×8×8ユニットであれば1ユニットの嵌合部が使えるのでより多くのパターンが考えられる。
しかし、シンプルな現在のパターンは5×5×5ユニットでなければ考えられなかった貴重なパターンなので変えたくない。

2)、6×6×6ミニキューブユニットの新対角線対称形ピース
8×8×8ミニユニットの空洞部を埋める6×6×6ミニユニットの各面の対角線対称形のピースのパターンは4×4×4ユニットでは希少なパターンであったが、嵌合部が少なかったので新たに6×6×6ユニットで開発した。
窓の部分に手持ちのハーフキューブをはめ込んでいるが、こうすると小物入れの箱になる。

3)、ミクロユニットによる6×6×6ユニットと4×4×4ユニットの対角線対称形パターン
6×6×6ミニユニットボックスの空洞部を埋めるために、手元にあった10mm角棒を使って一辺が当初キューブの3分の1のミクロユニットの
6×6×6ユニットの前項と異なる新対角線対称形パターンを開発した。
さらに、同じミクロユニットを使って6×6×6ユニットの空洞を埋めるために4×4×4ユニットの対角線対称形パターンのピースを作成した。

4)、すべて形状の異なる対角線対称形ピースによる4重のマトリョーシカ(入れ子)立体パズルの完成
以上述べてきたように2種類の角棒を材料として、すべて形状の異なる4パターン、24種類のこれまで世の中に存在しなかった、1軸対角線対称形のピースによる4重入れ子の立体パズルが完成した。
なお、これまで紹介してきた線対称形ピースによる立体パズルに関しては「1年間の発明の新規性の喪失の例外規定」の適用を受けて知財権を登録しています。
5、新しいキャビティキューブ(Boxタイプ)パズル
1)、ヒント
ツイッターでフォローしているパズルコレクターのたに~さんがお茶のりさんデザインの"Orion"を紹介されていた。

4つのピースを中央のフレームにはめ込むパズルだが、上面の凹凸のデザインが素敵なので、6面全てをこのデザインとした組み立てキューブパズルを開発することにした。
このパズルの名称がなぜ”Orion”なのか疑問に思ったのでAIチャットで検索してみた。
【オリオン座の形と名前の由来は、ギリシア神話の登場人物オーリーオーンにちなんでいます¹。オーリーオーンは海の神ポセイドーンの子で、優れた猟師だったとされています。しかし、自分が倒せない獲物はいないと思い上がり、女神ヘーラに怒られてさそりに刺されて死んでしまいました。その後、オーリーオーンとさそりは天に上げられて星座になりました。
オリオン座は冬の夜空に美しく輝く星座で、赤い1等星ベテルギウスと青白い1等星リゲルを含む7つの明るい星が特徴的です。中でも、三つ並んだ2等星δ星、ε星、ζ星は「オリオンのベルト」と呼ばれています。また、ベルトの下にあるc星、θ星とオリオン大星雲、ι星からなる3つの星と星雲は「小三つ星」と呼ばれています。
オリオン座は他の星座を見つける目印にもなります。例えば、オリオンのベルトを南東に延ばすと全天で最も明るい恒星シリウスが見つかります。シリウスはおおいぬ座の一部です。また、ベテルギウスとシリウスとこいぬ座のプロキオンを結ぶ正三角形は「冬の大三角」と呼ばれています】
どうやら、オリオン座の星全体を囲った形か、もしかしたら、中央のフレームを「オリオンのベルト」と見立てられたのかもしれない。
私は上面のデザインを敬意をこめて「オリオン模様」とよぶことにした。
2)、試作
キューブはキャビティキューブ(Boxタイプ)とし、まず、8分割したコーナーピースを作成した。

うまくいきそうなので、コーナーピースを3個の平面型ピースに分解することにした。

3種、24個のピースを作成し、誰かさんにヒント無しで6×6×6ユニットのキャビティキューブに組み立ててもらった。すると、予想外に数分で組み立ててしまった。しかも、底面と上面が「オリオン模様」になっていた。改めて、6面全てを同じ模様にする問題を出したところ、しばらくしてあきらめてしまった。

3、新しい組立てパズル「GENPEI」誕生


AIチャットの回答で、望遠鏡もなかった昔から肉眼で見つけた星に和名を付けていたことを知ったので、ピースを紅白に彩色して、パズルの名称を《GENPEI 》とした。
6面全てを同じ模様にするのを大正解とする、新しい組立てキャビティキューブパズルが完成した。
【岐阜県揖斐郡横蔵村(現・揖斐川町)には、オリオン座のリゲルとベテルギウスの色を源平の旗の色に喩えた言い回しが伝わっていたことを1956年ころに香田壽男によって採集されていたが、これは青白いリゲルを「平家星」、赤いベテルギウスを「源氏星」とするもので、一般に伝えられる源平の旗の色とは色の組み合わせが逆となっていた。現在では「源氏星」はリゲルの、「平家星」はベテルギウスの和名として知られている。】
注) 文中のAIチャットとは「 Microsoft Bring AI Chat」のことであるが、一部省略、加筆している。
6、新製品 ポリ(オミノ)タイルパズル
最近(2024年4月)、筆者の頭は出足でつまずいた阪神タイガースと、今年を人生最後の山登りと定めた石鎚山登山のことでいっぱいになっていて、新製品開発のアイデアは枯渇したと思っていました。
しかし、先日、夜中に起きていったトイレの中で突然、グッドアイデアが降りてきました。
これまで立方体が面同士でいくつかくっついたポリキューブをピースとして、様々な組立てキューブパズルを開発してきました。最近では対角線対称ピース(ポリキューブ)を見い出して、組立てボックス(キャビティキューブ)パズルを開発しました。また、キューブをハーフキューブやより厚みの薄いタイルに置き換えて、小資材化も果たしました。
正方形(スクェア)を辺同士でいくつかくっついたものはポリオミノと言いますので、厚みの薄いタイルは便宜上ポリオミノタイルと呼ぶことにします。
ポリ(オミノ)タイルのピースはキューブピースのようにユニットスクェアピースを接着剤で接合すると強度が落ちますので、ワンピースを切り取って作ります。
糸鋸でも作れますが、厚みが薄い特徴を生かせば、レーザー切断加工が最適であることに気づきました。
また、製品として直ぐに思いつくのは厚紙のジクソーパズルですが、私の過去の開発の中に画期的なアイデアがありました。
究極のマルチキューブパズルの私の好きな数式【(3の3乗)+(4の3乗)+(5の3乗)=(6の3乗)】のスライスキューブパズルです。
つまり、ポリキューブピースをそのままポリ(オミノ)タイルピースに置き換えるだけでいいのです。切断データを作り、例えば素材をMDF板にして、レーザー加工で切断すれば簡単に新商品が誕生するのです。
しかし、このままでは面白くないので、(3の3乗)、(4の3乗)、(5の3乗)のピースの上面を例えば、各青、緑、黄で着色し、これらすべてのピースを使う(6の3乗)は裏面(赤色)に限定することにしました。
さあ大変、まず、(6の3乗)を決めて裏面だけではどうしても(5の3乗)が出来ないのです(非対称形のピースは表と裏が異なる形になる)。あきらめきれないので、逆に(3の3乗)、(4の3乗)、(5の3乗)を決めて、(6の3乗)を新しく組み直すことにしました。
試行錯誤して3日かかりましたが、奇跡的に昨日完成しました。
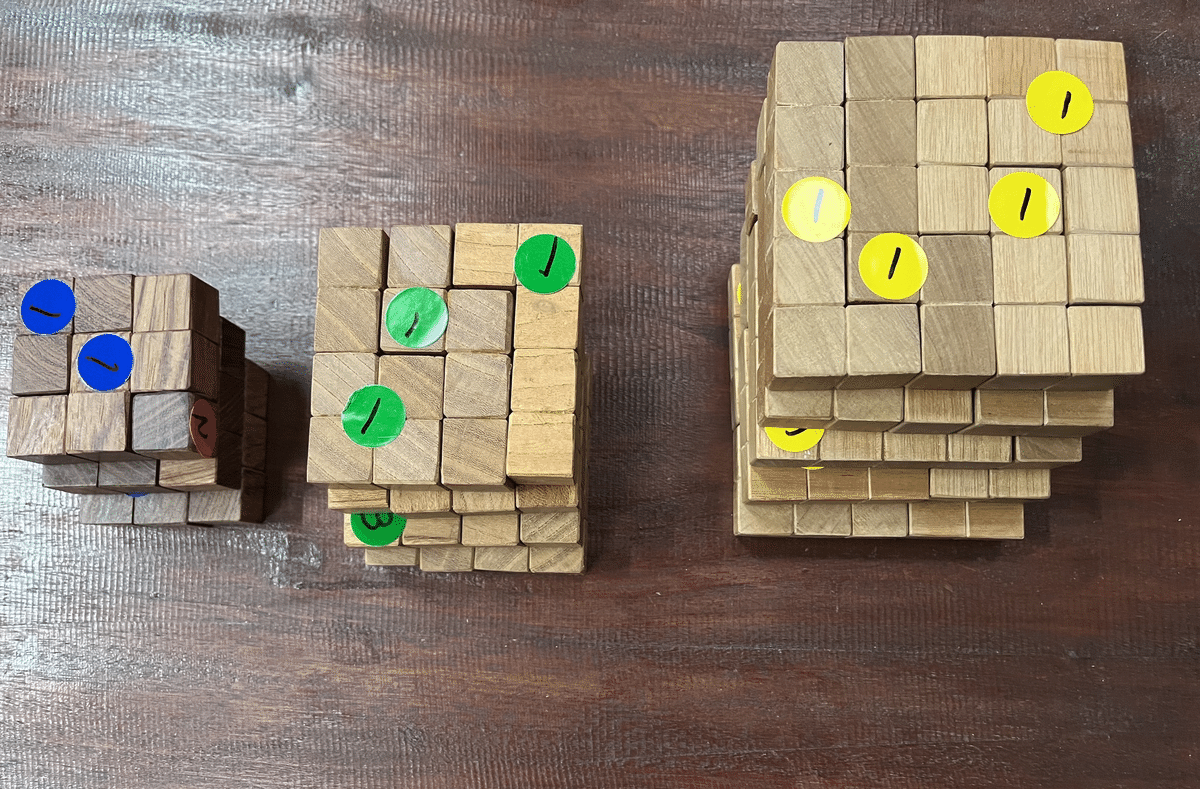

新製品 ポリ(オミノ)タイルパズル
(6cm四方タイル3枚)+(8cm四方タイル4枚)+(10cm四方タイル5枚)=12cm四方タイル6枚
1、片面が青色のピース(ポリタイル)7個で6cm四方のタイルを3枚組み立てて、青い台紙の上に積み上げて下さい。
2、片面が緑色のピース13個で8cm四方のタイルを4枚組み立てて緑色の台紙に積み上げて下さい。
3、片面が黄色のピース21個で10cm四方のタイルを5枚組み立てて、黄色の台紙の上に積み上げて下さい。
4、以上1から3の全てのピースの赤色面を上にして、12cm四方のタイルを6枚組み立てて、赤い台紙の上に積み上げて下さい。
* 青 大変易しい、緑 易しい、黄 少し難しい、赤 大変難しい
* 各台紙の裏面に解答例を示していますが、できるだけ見ないで頑張ってください。


あとがき
2024年5月現在、65歳でリタイアして17年になります。 日曜画家から絵描きになり、玉野市宇野の駅東創庫にオープンアトリエを構え、ショップも開いています。 10年前からもっぱら木のパズルやゲームに愛が芽生え、開発(創作)に熱中してきました。その間、知財権の出願は10件を超えましたが、商品化出来たものはパズルとゲーム各1件にとどまり、個人事業主としては赤字が続いています。
一方、著名な小黒三郎氏(1933年生まれ)は、動物組み木を開発されてからはビジネスと国内外の普及に大成功されています。以前、倉敷に滞在されていたこともあり、存じ上げていましたが、お仕事の内容に関しては無頓着でした。今後の参考にしたいと思い、ネットで著書「組み木の夢」を手に入れました。
この本で「動物組み木のおもちゃづくりは小学生からお年寄りまででき、作ることが楽しいことを僕は自ら知っているので、これまで数冊の作品集をとおして、作り方と制作図面を公開してきました。(中略)
糸のこでおもちゃを作ることによって、老人と子供がつながってゆくことは、老人に生きがいを与える、大きな力になると思います。組み木のおもちゃづくりを試しみたいという施設があれば、僕は大いに協力したいとおもっています。」(29ページ)と普及活動の基本的な考えを述べられています。
また、パズルについても、「パズルの世界は非常に難解なものと、誰もが親しめる、機知やユーモアに富むものとがあります。矛盾するようですが、この専門性と大衆性のパズルの二面性がパズルの世界を奥深いものとし、また多くの人になじむ普遍性を獲得してゆくのだと思います。(中略)
パズルは多くの老若男女や子供たちを遊びの世界にみちびく重要な水先案内人と考えています。」(121ページ)と述べられています。
このような考えをもとに、北海道から沖縄まで精力的を講演やワークショップをして回られるとともに、「遊プラン」などの会社を設立して、新製品の開発や製品製造のネットワークを拡大されてきています。
筆者も小黒氏の普及活動とビジネスの成功を見習って、残り少ない時間ではあるが、頑張って後進に夢を託していきたいと思っています。
(2024年7月記)
