スチュワートの定理

定理

定理1（スチュワートの定理）      三角形 $${\triangle\mathrm{ABC}}$$ の辺 $${\mathrm{BC}}$$ 上の点 $${\mathrm{P}}$$ について

$$
\mathrm{CP}\cdot\mathrm{AB}^2+ \mathrm{BP}\cdot\mathrm{AC}^2
= \mathrm{BC}\left(\mathrm{BP}\cdot\mathrm{CP}+\mathrm{AP}^2\right)
$$

が成り立つ.

上のスチュワートの定理からすぐにパップスの中線定理として知られる定理が得られる.

定理2（中線定理）     三角形 $${\triangle\mathrm{ABC}}$$ において辺 $${\mathrm{BC}}$$ の中点を $${\mathrm{M}}$$ とすると

$$
\mathrm{AP}^2
= \frac{\mathrm{AB}^2}2+\frac{\mathrm{AC}^2}2-\frac{\mathrm{BC}^2}4
$$

が成り立つ.

証明     スチュワートの定理より

$$
\mathrm{CM}\cdot\mathrm{AB}^2+ \mathrm{BM}\cdot\mathrm{AC}^2
= \mathrm{BC}\left(\mathrm{BM}\cdot\mathrm{CM}+\mathrm{AM}^2\right)\\
$$

$${\displaystyle \mathrm{BM}=\mathrm{CM}=\frac{\mathrm{BC}}2}$$ だから

$$
\begin{array}{rcl}\displaystyle
\frac{\mathrm{BC}}2\cdot\mathrm{AB}^2+ \frac{\mathrm{BC}}2\cdot\mathrm{AC}^2
&=&\displaystyle \mathrm{BC}\left(\frac{\mathrm{BC}}2\cdot\frac{\mathrm{BC}}2+\mathrm{AM}^2\right)\\
\mathrm{AB}^2+\mathrm{AC}^2 &=&\displaystyle 2\left(\frac{\mathrm{BC}^2}4+\mathrm{AM}^2\right)\\
\mathrm{AM}^2 &= &\displaystyle \frac{\mathrm{AB}^2}2+\frac{\mathrm{AC}^2}2-\frac{\mathrm{BC}^2}4\quad \Box
\end{array}
$$

証明

この節ではいくつかの方法でスチュワートの定理の証明をする.

初等的証明

ここで言う初等的とは三角法（三角関数）, 座標, ベクトル, 複素平面などの比較的新しい数学的道具を使わずに証明することをである.

頂点 $${\mathrm A}$$ から辺（直線） $${\mathrm{BC}}$$ に下した垂線の足を $${\mathrm{H}}$$
とする.
点 $${\mathrm{P}}$$ は $${\mathrm{BH}}$$ 上かまたは $${\mathrm{CH}}$$ 上にある.
$${\mathrm{P}}$$ が $${\mathrm{BH}}$$ 上にあるとしても一般性を失わない.

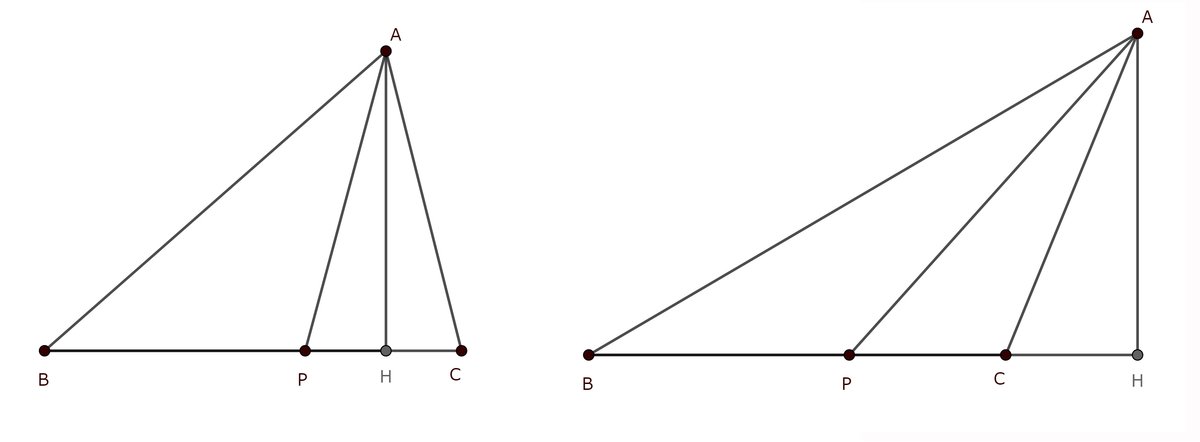
$${\mathrm{H}}$$ が辺 $${\mathrm{BC}}$$ 上にあるとき(図の左), $${\mathrm{BH}=\mathrm{BP}+\mathrm{PH}}$$, $${\mathrm{CH}=\mathrm{CP}-\mathrm{PH}}$$ であり, $${\mathrm{H}}$$ が辺 $${\mathrm{BC}}$$ の外にあるとき(図の右), $${\mathrm{BH}=\mathrm{BP}+\mathrm{PH}}$$, $${\mathrm{CH}=\mathrm{PH}-\mathrm{CP}}$$ である.     いずれの場合も $${\mathrm{CH}^2=\left(\mathrm{CP}-\mathrm{PH}\right)^2}$$ が成り立つ.     3つの直角三角形 $${\triangle\mathrm{APH}}$$, $${\triangle\mathrm{ABH}}$$, $${\triangle\mathrm{ACH}}$$ にピタゴラスの定理を用いる.

$$
\begin{array}{rcl}\displaystyle
\mathrm{AP}^2 &=& \mathrm{PH}^2+\mathrm{AH}^2\\
\mathrm{AB}^2 &=& \mathrm{BH}^2+\mathrm{AH}^2 =
\left(\mathrm{BP}+\mathrm{PH}\right)^2+\mathrm{AH}^2\\
\mathrm{AC}^2 &=& \mathrm{CH}^2+\mathrm{AH}^2 =
\left(\mathrm{CP}-\mathrm{PH}\right)^2+\mathrm{AH}^2
\end{array}
$$

これより

$$
\begin{array}{rcl}\displaystyle
\mathrm{AB}^2 &=&
\mathrm{BP}^2+2\mathrm{BP}\cdot\mathrm{PH}+\mathrm{AP}^2\\
\mathrm{AC}^2 &=&
\mathrm{CP}^2-2\mathrm{CP}\cdot\mathrm{PH}+\mathrm{AP}^2
\end{array}
$$

この 2式から $${\mathrm{PH}}$$ を消去する.     

$$
\begin{array}{rcl}\displaystyle
\mathrm{CP}\cdot\mathrm{AB}^2+ \mathrm{BP}\cdot\mathrm{AC}^2
&=&\mathrm{CP}\left(\mathrm{BP}^2+\mathrm{AP}^2\right)
+\mathrm{BP}\left(\mathrm{CP}^2+\mathrm{AP}^2\right) \\
&=&\left(\mathrm{BP}+\mathrm{CP}\right)
\left(\mathrm{BP}\cdot\mathrm{CP}+\mathrm{AP}^2\right)
\end{array}
$$

$${\mathrm{BP}+\mathrm{CP}=\mathrm{BC}}$$ だから

$$
\mathrm{CP}\cdot\mathrm{AB}^2+\mathrm{BP}\cdot\mathrm{AC}^2
=\mathrm{BC}\left(\mathrm{BP}\cdot\mathrm{CP}+\mathrm{AP}^2\right)\quad\Box
$$

三角法による証明

$${\angle\mathrm{APB}=\theta}$$ とおく.     $${\angle\mathrm{APC}=180^{\circ}-\theta}$$ である.     2つの三角形 $${\triangle\mathrm{ABP}}$$ と $${\triangle\mathrm{ACP}}$$ に余弦定理を用いる.

$$
\begin{array}{rcl}\displaystyle
\mathrm{AB}^2 &=&
\mathrm{AP}^2+\mathrm{BP}^2-2\mathrm{AP}\cdot\mathrm{BP}\cos\theta\\
\mathrm{AC}^2 &=&
\mathrm{AP}^2+\mathrm{CP}^2-2\mathrm{AP}\cdot\mathrm{CP}\cos(180^{\circ}-\theta)\\
\mathrm{AC}^2&=&
\mathrm{AP}^2+\mathrm{CP}^2+2\mathrm{AP}\cdot\mathrm{CP}\cos\theta
\end{array}
$$

ここから $${\cos\theta}$$ を消去する.

$$
\begin{array}{rcl}\displaystyle
\mathrm{CP}\cdot\mathrm{AB}^2+ \mathrm{BP}\cdot\mathrm{AC}^2
&=&\mathrm{CP}\left(\mathrm{AP}^2+\mathrm{BP}^2\right)
+\mathrm{BP}\left(\mathrm{AP}^2+\mathrm{CP}^2\right) \\
&=&\mathrm{BC}\left(\mathrm{BP}\cdot\mathrm{CP}+\mathrm{AP}^2\right)\quad\Box
\end{array}
$$

ベクトルによる証明

$${\mathrm{BC}=a}$$, $${\mathrm{BP}=x}$$, $${\mathrm{CP}=y}$$ とおく.

$$
y \mathrm{AB}^2+x \mathrm{AC}^2 = a\left(\mathrm{AP}^2+xy\right)
$$

を示せばよい.     $${a=x+y}$$ である.

$$
\begin{array}{rcl}\displaystyle
a^2 &=& \overrightarrow{\mathrm{BC}}\cdot\overrightarrow{\mathrm{BC}}
=\left(\overrightarrow{\mathrm{AC}}-\overrightarrow{\mathrm{AB}}\right)
\cdot\left(\overrightarrow{\mathrm{AC}}-\overrightarrow{\mathrm{AB}}\right)\\
&=&\overrightarrow{\mathrm{AB}}\cdot\overrightarrow{\mathrm{AB}}
+\overrightarrow{\mathrm{AC}}\cdot\overrightarrow{\mathrm{AC}}
-2\overrightarrow{\mathrm{AB}}\cdot\overrightarrow{\mathrm{AC}}\\
&=& \mathrm{AB}^2+\mathrm{AC}^2
-2\overrightarrow{\mathrm{AB}}\cdot\overrightarrow{\mathrm{AC}}
\end{array}
$$

よって

$$
\overrightarrow{\mathrm{AB}}\cdot\overrightarrow{\mathrm{AC}}
= \frac12\left(\mathrm{AB}^2+\mathrm{AC}^2-a^2\right)\quad\cdots\,(1)
$$

である.
点 $${\mathrm P}$$ は線分 $${\mathrm{BC}}$$ を $${x:y}$$ に内分する点だから

$$
\displaystyle
\overrightarrow{\mathrm{AP}} =
\frac{y \overrightarrow{\mathrm{AB}}+x\overrightarrow{\mathrm{AC}}}{x+y}
=\frac ya\overrightarrow{\mathrm{AB}}+\frac xa \overrightarrow{\mathrm{AC}}
$$

したがって

$$
\begin{array}{rcl}\displaystyle
\mathrm{AP}^2
& =& \overrightarrow{\mathrm{AP}}\cdot\overrightarrow{\mathrm{AP}}
\left(\frac ya\overrightarrow{\mathrm{AB}}+\frac xa \overrightarrow{\mathrm{AC}}\right)
\cdot
\left(\frac ya\overrightarrow{\mathrm{AB}}+\frac xa \overrightarrow{\mathrm{AC}}\right)\\
&= &\displaystyle \frac{y^2}{a^2}\mathrm{AB}^2+ \frac{x^2}{a^2}\mathrm{AC}^2+
\frac{2xy}{a^2}\overrightarrow{\mathrm{AB}}\cdot\overrightarrow{\mathrm{AC}}
\end{array}
$$

(1) より

$$
\begin{array}{rcl}\displaystyle
\mathrm{AP}^2 &= &\displaystyle \frac{y^2}{a^2}\mathrm{AB}^2+ \frac{x^2}{a^2}\mathrm{AC}^2+
\frac{2xy}{a^2}\frac12\left(\mathrm{AB}^2+\mathrm{AC}^2-a^2\right)\\
&= &\displaystyle\frac{y(x+y)}{a^2}\mathrm{AB}^2+\frac{x(x+y)}{a^2}\mathrm{AC}^2-xy
\end{array}
$$

$${a=x+y}$$ より

$$
y \mathrm{AB}^2+x \mathrm{AC}^2 = a\left(\mathrm{AP}^2+xy\right)\quad\Box
$$

複素平面による証明

点 $${\mathrm{P}}$$ を原点とし $${\mathrm{B}}$$ が実軸上負の位置に, $${\mathrm{C}}$$ が実軸上正の位置になるようにすると $${\mathrm{B, C}}$$ を表す複素数はそれぞれ $${-x}$$ と $${y}$$ になる.      頂点 $${\mathrm{A}}$$ を表す複素数を $${\omega}$$ とおくと

$$
\begin{array}{lcl}
\displaystyle\mathrm{AP}^2 & = &\displaystyle \left|\omega\right|^2\, =\,
\omega \overline{\omega}\\
\displaystyle\mathrm{AB}^2 & = &\displaystyle
\displaystyle (\omega+x)\overline{(\omega+x)}\\
\displaystyle\mathrm{AC}^2 & = &\displaystyle
\displaystyle(\omega-y)\overline{(\omega-y)}\\
\end{array}
$$

と表される.

$${x,y}$$ が実数であること, $${a=x+y}$$ に注意すると

$$
\begin{array}{rcl}\displaystyle
y \mathrm{AB}^2+x \mathrm{AC}^2 &=&
y(\omega+x)\left(\overline{\omega}+x\right)
+x(\omega-y)\left(\overline{\omega}-y\right)\\
&= &\displaystyle\displaystyle (x+y) \omega\overline{\omega}+x^2y+xy^2
\, = \, a\left(\mathrm{AP}^2+xy\right) \quad\Box
\end{array}
$$

独り言

初等的証明と三角法による証明を比べると余弦定理がピタゴラスの一般化になっていることがよくわかる.

三角法による証明では 2つの三角形に注目して証明を展開したのに対して,
ベクトルによる証明と複素平面による証明では計算をするだけで証明が完結している印象である.

複素平面による証明が他の方法に比べて簡潔で優れていると思うのは早合点である.
他の 3つの証明では $${\mathrm{AP}^2}$$ を求める方向で議論を進めていてスチュワートの定理の結論の式を知らなくても結果として定理の得ることができるのに対して, 複素平面による証明では結論の式を確認する計算をしているので結論の式ありきの議論になっている.     実際, ベクトルによる証明で
$${-y\overrightarrow{\mathrm{PB}}=x\overrightarrow{\mathrm{PC}}}$$
という関係を用いて

$$
y \overrightarrow{\mathrm{AB}}\cdot\overrightarrow{\mathrm{AB}} +x \overrightarrow{\mathrm{AC}}\cdot\overrightarrow{\mathrm{AC}}
=a\left(\overline{\mathrm{PA}}\cdot\overline{\mathrm{PA}}+xy\right)
$$

を示すことができる.
また, $${\mathrm A}$$ を原点として点 $${\mathrm{B, C, P}}$$ を表す複素数をそれぞれ
$${\beta, \gamma, \rho}$$ とおくとベクトルによる証明と同じような計算で

$$
|\rho|^2 = \frac ya |\beta|^2 + \frac xa |\gamma|^2-xy
$$

を導くことができる.

この文書の PDF ファイルは有料です。