三角関数・複素数の問題 2025/1/22 解答

受験生向けの問題です。     1番は三角関数, 2番は複素数の問題です、見かけは違うけどモチーフは同じです。

問題

問題1

辺 $${\mathrm{AD}}$$ と辺 $${\mathrm{BC}}$$ が平行の台形 $${\mathrm{ABCD}}$$ において $${\mathrm{AD}=a}$$, $${\mathrm{BC}=b}$$, $${\mathrm{AB}=a+b}$$     $${a \leqq b}$$とする.      $${\angle\mathrm{A}}$$ の 2等分線と $${\angle\mathrm{B}}$$ の 2等分線の交点を $${\mathrm P}$$ とする.     $${\angle\mathrm{BAP}=\theta}$$ とおく. 
     (1)  $${\mathrm{DP}}$$ を求めよ.
     (2)  $${\displaystyle\frac{\mathrm{CP}+\mathrm{DP}}{\mathrm{CD}}}$$ を求めよ.

問題2

$${\omega = \cos\theta + i\sin\theta}$$   $${\displaystyle\left(0 < \theta < \frac{\pi}2\right)}$$ とおく.     複素数平面において $${(1-a)\omega^2}$$ と $${1+a\omega^2}$$ を表す点をそれぞれ $${\mathrm{A, B}}$$ とする.     線分 $${\mathrm{AB}}$$ 上の点 $${z}$$ が $${\arg z=\theta}$$ を満たしている.     $${z-1}$$ を極形式で表せ.     ただし, $${a}$$ は $${0 < a < 1}$$ の実数である.

解答

問題1

(1)

$${\mathrm{AB}}$$ と $${\mathrm{CD}}$$ が平行なので $${A+B=\pi}$$ であり, $${\triangle\mathrm{ABP}}$$ は $${\angle\mathrm{APB}}$$ が直角の直角3角形である （図1 左）.     よって

$$
\mathrm{AP}=\mathrm{AB}\cos\theta=(a+b)\cos\theta
$$

である.     $${\triangle\mathrm{APD}}$$ に余弦定理を用いる.

$$
\begin{array}{lcl}
\mathrm{DP}^2&= &
\mathrm{AD}^2+\mathrm{AP}^2-2\mathrm{AD}\cdot\mathrm{AP}\cos\theta\\
&=&a^2+(a+b)^2\cos^2\theta-2a(a+b)\cos^2\theta\\
&=&a^2+(b^2-a^2)\cos^2\theta\\
\mathrm{DP} &= & \sqrt{a^2+(b^2-a^2)\cos^2\theta}
\end{array}
$$

(2)

$${\triangle\mathrm{BPC}}$$ に余弦定理を用いる.

$$
\begin{array}{lcl}
\mathrm{CP}^2&= &
\mathrm{BC}^2+\mathrm{BP}^2
-2\mathrm{BC}\cdot\mathrm{BP}\cos\left(\frac{\pi}2-\theta\right)\\
&=&b^2+(a+b)^2\sin^2\theta-2b(a+b)\sin^2\theta\\
&=&b^2+(a^2-b^2)(1-\cos^2\theta)\\
&=&a^2+(b^2-a^2)\cos^2\theta\\
\mathrm{CP} &= & \sqrt{a^2+(b^2-a^2)\cos^2\theta}
\end{array}
$$

よって $${\mathrm{CP}+\mathrm{DP}=2\mathrm{CP}}$$ である.

辺 $${\mathrm{BC}}$$ 上に点 $${\mathrm E}$$ を $${\mathrm{EC}=\mathrm{AD}}$$ となるようにとると四角形 $${\mathrm{AECD}}$$ は平行四辺形である.     $${\triangle\mathrm{ABE}}$$ に余弦定理を用いる.

$$
\begin{array}{lcl}
\mathrm{CD}^2&= & \mathrm{AE}^2 , = ,
\mathrm{AB}^2+\mathrm{BE}^2
-2\mathrm{AB}\cdot\mathrm{BE}\cos\left(\pi-2\theta\right)\\
&=&(a+b)^2+(b-a)^2\sin^2\theta+2(a+b)(b-a)\cos2\theta\\
&=& 2a^2+2b^2+2(b^2-a^2)(2\cos^2\theta-1)\\
&=&4\left(a^2+(b^2-a^2)\cos^2\theta\right)\\
\mathrm{CD} &= & 2\sqrt{a^2+(b^2-a^2)\cos^2\theta}
\end{array}
$$

したがって $${\displaystyle \frac{\mathrm{CP}+\mathrm{DP}}{\mathrm{CD}}=1}$$ である.

図1 問題1

問題2

$${z}$$ は線分 $${\mathrm{AB}}$$ 上の点だから

$$
z-(1-a)\omega^2=s(1+a\omega^2-(1-a)\omega^2)\quad 0<s<1
$$

を満たすような実数 $${s}$$ が存在する.

$$
\begin{array}{lcl}
z & = & (1-a)\omega^2+s(1+a\omega^2-(1-a)\omega^2)\\
&=& s+(s(2a-1)+1-a)\omega^2
\end{array}
$$

さらに $${\arg z=\theta}$$ だから

$$
z = t\omega \quad t>0
$$

を満たす実数 $${t}$$ が存在する.     よって

$$
\begin{array}{lcl}
s+(s(2a-1)-a)\omega^2&= & t\omega \\
s\overline{\omega}+(s(2a-1)+1-a)\omega^2\overline{\omega}
&=& t\omega\overline{\omega}\\
\end{array}
$$

$${\omega\overline{\omega}=1}$$ より

$$
s\overline{\omega}+(s(2a-1)+1-a)\omega = t\\
$$

両辺の虚数部分を比較する.

$$
\begin{array}{lcl}
-s\sin\theta+(s(2a-1)+1-a)\sin\theta &=& 0\\
(a-1)(2s-1)\sin\theta &=& 0
\end{array}
$$

$${a<1}$$, $${0<\sin\theta}$$ だから $${\displaystyle s=\frac12}$$ であり

$$
\begin{array}{lcl}
z & = & \displaystyle\frac12(1+\omega^2)\\[3mm]
& = & \displaystyle\frac12\left(1+(\cos\theta+i\sin\theta)^2\right)\\[3mm]
&= & \displaystyle\frac12\left(1+\cos^2\theta -\sin^2\theta
+2i\cos\theta\sin\theta\right)\\[3mm]
&= & \displaystyle\frac12\left(2\cos^2\theta +2i\cos\theta\sin\theta\right)
\\[3mm]
&= & \displaystyle \cos^2\theta +i\sin\theta\cos\theta\\[5mm]
z-1&= & \displaystyle \cos^2\theta-1 +i\sin\theta\cos\theta\\
&=&\displaystyle -\sin^2\theta +i\sin\theta\cos\theta\\
&=&\displaystyle \sin\theta(-\sin\theta +i\cos\theta)\\[3mm]
&=&\displaystyle \sin\theta\left(\cos\left(\theta+\frac{\pi}2\right)
+i\sin\left(\theta+\frac{\pi}2\right) \right)
\end{array}
$$

独り言

作問のモチーフとなった命題を紹介する.

命題     辺 $${\mathrm{AD}}$$ と $${\mathrm{BC}}$$ が平行な台形 $${\mathrm{ABCD}}$$ が $${\mathrm{AB}=\mathrm{AD}+\mathrm{BC}}$$ を満たすとき, $${\angle\mathrm{A}}$$ と $${\angle\mathrm{B}}$$ の 2等分線と辺 $${\mathrm{CD}}$$ は共点をもつ.

先の問題はどちらもこの命題を三角法や複素平面を用いて証明する過程を問題化したものである.

問題1 では $${\angle\mathrm{A}}$$ の 2等分線と $${\angle\mathrm{B}}$$ の 2等分線の交点 $${\mathrm P}$$ について $${\mathrm{CP}+\mathrm{DP}=\mathrm{CD}}$$ を示すことにより点 $${\mathrm{P}}$$ が辺 $${\mathrm{CD}}$$ 上にあることを証明した.     さらに $${\mathrm{CP}=\mathrm{DP}}$$ だから $${\mathrm P}$$ は辺 $${\mathrm{CD}}$$ の中点であることを示している.

問題2 では複素数平面の原点, $${1}$$, $${1+a\omega^2}$$, $${(1-a)\omega^2}$$ がそれぞれ命題の頂点 $${\mathrm{A, B, C, D}}$$ に対応している.     このとき, $${z}$$ は $${\angle\mathrm A}$$ の 2等分線と辺 $${\mathrm{CD}}$$ の交点であり, $${z-1}$$ の偏角を調べることにより命題の結論を導くことができる.

問題で取り上げた方法以外の命題の証明について触れておく.

証明1

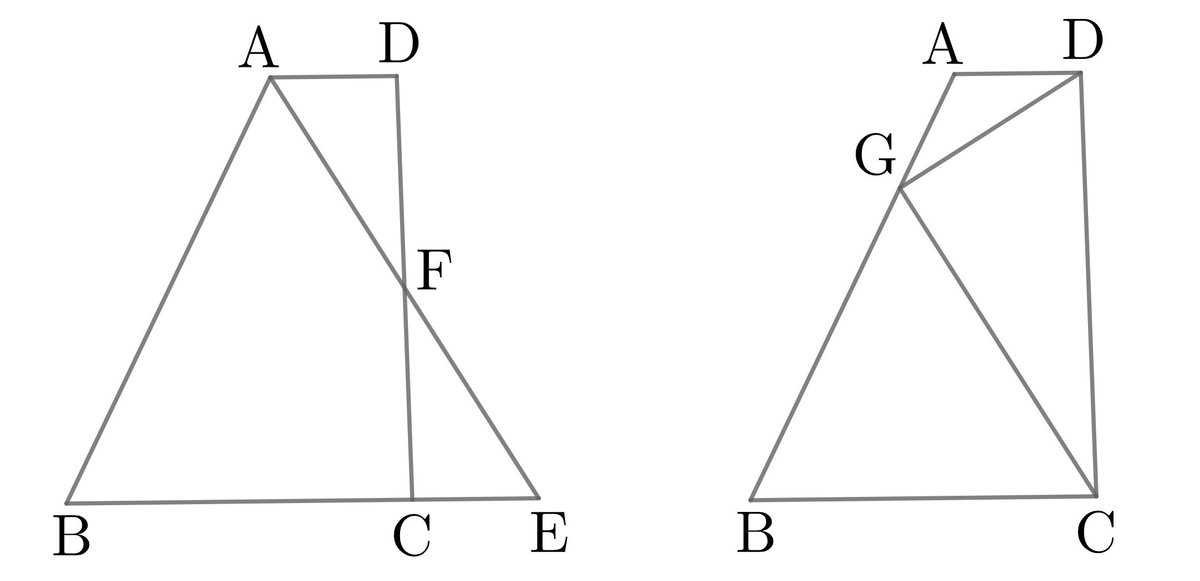
辺 $${\mathrm{BC}}$$ を頂点 $${\mathrm C}$$ の方に延長した直線上に点 $${\mathrm E}$$ を $${\mathrm{CE}=\mathrm{AD}}$$ となるように定め, $${\mathrm{AE}}$$ と辺 $${\mathrm{CD}}$$ の交点を $${\mathrm F}$$ とする（図2 左）.

すると, $${\triangle\mathrm{ADF}}$$ と $${\triangle\mathrm{ECF}}$$ は合同であることがわかる.      さらに, $${\mathrm{AE}}$$ は $${\angle\mathrm A}$$ の 2等分線であることと,  $${\mathrm{BF}}$$ が $${\angle\mathrm{B}}$$ の2等分線であることが示せる.     
詳しくは有料の PDF ファイルで議論する.

証明2

辺 $${\mathrm{AB}}$$ 上に点 $${\mathrm G}$$ を $${\mathrm{AG}=\mathrm{AD}}$$ となるように定める（図2 右）.

このとき, $${\angle\mathrm A}$$ と $${\angle\mathrm B}$$ の2等分線はそれぞれ $${\mathrm{DG}}$$ と $${\mathrm{CG}}$$ の垂直2等分線になり, これら ２等分線の交点は $${\triangle\mathrm{DGC}}$$ の外心である.     $${\triangle\mathrm{DGC}}$$ は $${\mathrm{CD}}$$ を斜辺とする直角 3角形であり, 外心は $${\mathrm{CD}}$$ の中点である.
こちらも詳細は有料の PDF ファイルにある.

図2 命題の証明

命題のベクトルによる証明を有料の PDF で与える.
これを基に問題1 や問題2 のような問題を考えてみると新たな学びにつながることもあるだろう.     作問作業は数学の楽しみ方の一つかもしれないが, 仕事でするのはお勧めしない.     締め切りがなければ話は違うかもしれない.