
数学という存在
さて今日は数学の(やさしい)話をしたいと思います。中学1年生の数学の知識があれば理解できる話です。
みなさんは、円の面積や、円周の長さを計算したりできると思います。小学校で習っているはずです。
円の面積 = 円周率×半径×半径
円周の長さ = 円周率×直径
で、この式の証明はできますか?
いきなりど真ん中の質問をしました。では、言い換えます。そもそも“どんな円”でも、円周の長さは直径にある定数(円周率)を掛けたらよい、というのは自明なことでしょうか?そんな疑問を持ったことがありませんか。
例えば、1個10円の飴玉があったとします。10個買うと 10 × 10=100円ですね。で、100個買うと100 × 10= 1000円です…いいえ、1個無料になって990円になるかも知れません。さらに、1000個買うと10%引きになって10000 - 1000=9000円にしてもらえかも知れません。まあ、これは数学ではないと言う人もおるでしょうが…こういう式で表されます。
値段=個数× 10, 0 ≦ 個数< 100のとき
値段=個数×(10 - 0.1), 100 ≦ 個数< 1000のとき
値段=個数×(10 - 1), 1000 ≦ 個数のとき
わたしが言いたいのは、そんなふうに(飴玉の単価のように)、円周率は一定でなくて、半径によって変わるかも知れないんじゃないか…どんな大きさの円でも、円周の長さは正確に直径(または半径)に正比例するって本当に本当なの?って言うことなんです。もし本当なら〜本当と確信できたら〜これはスゴいことなのではないか…あやふやだったことが、確実になるのですからね。
殆どの人は、そんなあやふや感、ましてや疑問さえ持ったことがないと思います。なぜなら、先生や教科書のいうことを信じているからです。(でも、最近の教科書には円の面積の式を得る方法が書いてあるかも知れませんね。)
それではまず、面積の定義をしましょう。
縦横の長さがそれぞれ1の正方形の面積を1と定義します。
ある図形の面積は、この単位面積をいつく敷き詰められるかで決まります。例えば、縦2,横3の長方形なら、面積は2×3=6になります。
一般的にいうと…

長方形の面積=縦の長さ×横の長さ
A = ab
(思い出してください、abは a × b のことです。×は普通省略します)
では、この長方形を2倍に拡大します。つまり縦横それぞれ2倍にします。すると面積は
2a × 2b = 4ab = 4A
もとの4倍になりますね。
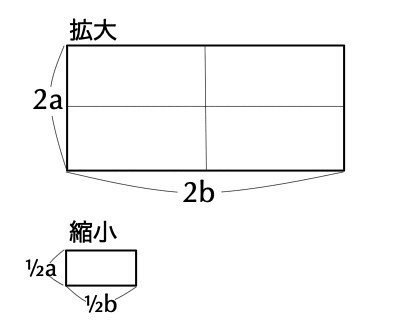
こんどは、もとの長方形を1/2に縮小すると、面積は
½a × ½b = ¼ab = ¼A
となりますね。
一般に、rを倍率とすると、
拡大・縮小後の面積 = r²ab (または r²A)
と書けます。
ではもっと一般的に、任意の図形を考えて見ましょう。例えば、これ…

この面積をAとしたとき、この図形を2倍あるいは r倍に拡大すると、新しい面積はどうなるでしょう。
ここに格子を描いて、この図形の内部の長方形を数えれば、“近似的な”面積が求まります。もっと小さな格子を描けば、もっと正確に面積が求まります。

内部に長方形がn個あり、長方形1個の面積がA₀とすると、この図形の面積の近似値は
nA₀
そこでこの図形を格子と一緒に拡大しましょう。r倍する。すると…

格子もr倍、つまり内部の長方形の面積は r² 倍になります(=r²A₀)。ということは、拡大された雲図形の近似面積は
n(r²A₀)
…入れ替えると、
r²(nA₀)
もっと細かい格子を描けば、もっと正確な面積が求まるけれど、結局、r倍に拡大・縮小すると、図形の面積は r² 倍になるっていうことだよねえ。
で、ここで、円に戻ります。

半径1の円があります。その面積をAとします。
この円をr倍に拡大または縮小するとその面積は、上の考え方で
r²A
になります。
そこでこのA すなわち“半径1の円の面積”をπと定義します。すると、半径rの円の面積は
πr²
となります。証明できました!
ちょっと待って、πって円周と直径の比ではなかったの?面積だなんて、初めて聞いた!そう、それは次の式
円周の長さ = 2πr
を証明すれば、そう云うかっこいい名前で呼べます。いまはまだ、さっきも言いましたように、円周と直径の間に比率があるのかどうかもわからない状態です。それまでは、πは「半径1の円の面積」という長ったらしい名前です。
(以上は数学的にいうと「図形の相似」の性質を説明したものです)
* * *
ここで、ちょっと一息つきましょう。
タバコでも一服してください。タバコを吸わない方は、コーヒーか紅茶でも用意しましょうね。
ここは、中学生には少しむずかしいかも知れませんので、読み飛ばしても構いませんよ。
数学についてよく聞く質問はこれです、「数学はなんの役に立つのか。」
これに対して科学者は普通こう答えます。
数学の大部分は、いつか有用になるだろういうことをまったく考えず、また知り得ない状況のなかで発展して来ました。
そうして、何十年とか、百何十年経って、有用性が発見されます。
こういうことは、科学の他の分野でも見られます。
しかもそれは、人が何かを求めて研究するというような功利主義よりも、予想もしない驚くべき成果をだしているのです。
有用性とはなんの関係もなく全体の事柄が動いているように見えるにもかかわらずです。
〜フォン・ノイマン 科学と社会における数学の役割〜から要約
個人的なことで言えば、例えば今わたしはこの記事を書いていますが、それは32年前に買って読んだ書物
サージ・ラング著「さあ数学しよう!」
の感動が元になっています(実際、ここの証明は、この書を元にしています)。その時は、こんな記事を書くことに使われるなど、考えもしなかったわけです。
あるいはまた、小さな子供が水たまりを見ます。すると子どもっていうのはすぐ水たまりに入って足でパシャピシャするんですね。子どもにとって別に何の目的もありません。大人から見れば、珍しいものを見て、体験とか発見をしているんだと見ることができるでしょうが…
人間は行きている中でいろいろやります、遊びとか、仕事とか…。
そうやっていく過程で、自分のやっている事柄の本質は何だろうと考えたり、一体何の目的でこういうことをやっているのかとか考えだすものです。
でも人間がその行動を始めたその動機こそ一番純粋なのではないかと思ったりします。(なんとなくやり始めて習慣になったというのもあるかも知れませんが…)
何かの役に立つからやり始めるということは確かにありますが、何か美しいものを感じたとか、単純に楽しいからとか、そういう動機もあると知っておいてもよいのではないかと思うのです。
そしてそれ(何の役にも立っていないもの)が個人を超えて、(数学というような体系のなかで)人類の資産となって受け継がれていくというのは、偉大なことなんだろうと思います。こうして、ばらばらにあった人類の知識がある時、論理的に繋げられる、つまり、証明、発明・発見、活用というようなことができるわけですから。
ちょっと別の話題になりますが、最近の「本がひらく」noteの記事
数学は複雑化する世界を生きぬくための必須のツール。数学による人生の指南書『公式より大切な「数学」の話…
に、
プラトン主義者と唯名論者の主張はたしかに大きく異なっているが、いずれの立場も数学のしくみ、もっと言うなら、人間が数学に取り組むと何が起こるかを説明しようとしている。
プラトン主義者によれば、そのとき人間は抽象的な事物で成り立つ世界についてあらゆる発見をするのだという。一方で唯名論者は、そんな世界は存在せず、すべて人間が発明していると主張する。この2つの考え方をはっきり区別でき、どちらが正しいのか決着がついていない…
と書いてありました。この2つの考え方(プラトン主義と唯名論)は異なるということですが、わたしは個人的に、どちらも結局同じに思います。
人間は何かに関与すると、何かを作り出すものだと思います。
何かというのは、上の引用の中の言葉でいうと抽象的な事物、つまり仮想の世界です。仮想の世界というのは幻であり故に客観的には存在しないと考えられていますが、人間の行動や考えというものは、ほぼ100%この自身が作った仮想世界が因となっているのではないでしょうか。
だとすれば、人間の考える仮想の世界は、存在しているのと同等の重みがあります。
上の引用は数学者が言っていることですから、間違いないことだと思いますが、まあ、こんな考えもあるのでは、という個人的な話です。
数学というものは、かたくるしく感じる方が多いと思いますが、本当はもっと人間的なものなのです。
* * *
道草しました。続けましょう。円周の長さcと半径rの関係式
c = 2πr
の証明です。
πはさっき言った「半径1の円の面積」で一定不変の数値です。
まず、半径rの円を描き、それより少し大きい円を重ねて描きます。

2つの円の間に帯ができます。この帯の面積を求めましょう。簡単です。
大きい円の面積 − 小さい円の面積
π(r+h)² - πr²
この式をもう少し計算しましょう。まず、(r+h)²は (r+h)(r+h)ということなので、(以下、分配法則を2回適用して)
(r+h)(r+h)
= r(r+h) + h(r+h)
= r²+rh + hr+h² (rh+hr は 2hr なので↓)
= r²+2rh+h²
すると上の式(円の帯の面積)は、
π(r+h)² - πr²
= π(r²+2rh+h²) - πr²
= πr² + 2πrh + πh² - πr² (πr² はプラスとマイナスで消える↓)
= 2πrh + πh²
となります。
ここで、長方形の帯を2つ作ります。

高さは両方とも h で、長さはそれぞれ、小さい円の周の長さ c と、大きい円の周の長さ c₂ とします。
そこで、短い方の帯を、先程の小さい円のまわりに巻きつけましょう。
立てて巻きつけるのじゃなくて、円の帯にペシャッと重ねましょう。できない?破れてしまいますからね。

では次に、長い方の帯を、大きい円の周りに巻きつけましょう。そして、円の帯に重ねます。今度は襞ができます。

つまり、短い帯の面積は、円の帯より小さいし、長い帯の面積は、円の帯より大きい。というわけで、次のような不等式が得られます。
短い帯の面積 ≦ 円の帯の面積 ≦ 長い帯の面積
hc ≦ 2πrh + πh² ≦ hc₂
そこで、この不等式全体を h で割ります。hは正の数なので不等号の向きは変わりません。
(hc)/h ≦ (2πrh + πh²)/h ≦ (hc₂)/h
h で約分しましょう。
c ≦ 2πr + πh ≦ c₂
ここで、h を0に近づけると、c₂ は小さい円周 c にどんどん近づきます。
他方真ん中の
2πr + πh
は、h→0になると、πh の項が0になります。結局
c ≦ 2πr ≦ c
従って、
c = 2πr
が証明できました!
これで、晴れてπを円周の長さと直径(半径)の比率、円周率とよぶことができます。最後まで付き合っていただき、ありがとうございました。お疲れさまでした。
【2020-8-31 少し修正】
この記事が気に入ったらサポートをしてみませんか?
