CNN(Convolutional Neural Network)の畳み込み処理をjavaで実装する
1. 概要
Convolutional Neural Network(CNN)では、画像の局所的な特徴を取り出し、抽象化する為に畳み込みレイヤーを用います。今回は、このCNNの畳み込み処理の概念を整理すると共に、javaでの実装方法について説明します(pythonでは既に丁寧に説明された文献がたくさんありますので、自己理解を深める為にあえてjavaを選んでみました)。畳み込み処理の演算には、行列の計算を用いますが、こちらは、nd4jというライブラリを用いることにしました。
1.1. 対象者
Convolutional Neural Networkの畳み込み処理の基本的なロジックについて実装ベースで学びたい人
2. 2次元畳み込み処理
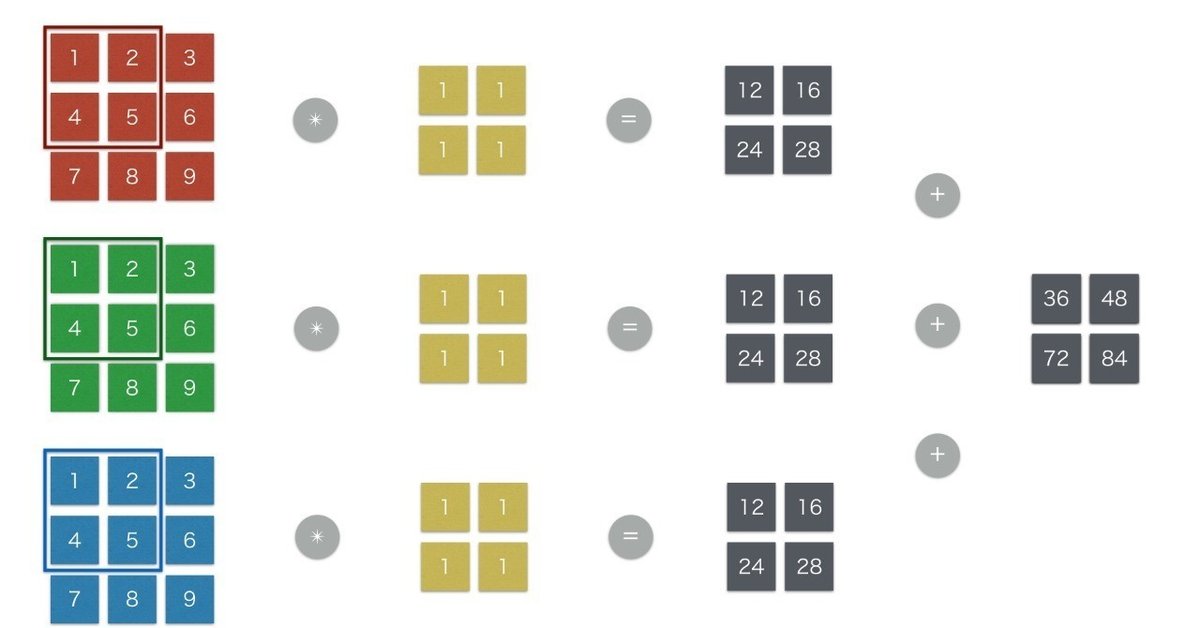
白黒の2値画像や、グレースケール画像のような縦横2次元で表現できるデータを入力データとして想定し、処理フローを確認していきます。入力データの畳み込み演算はカーネル(もしくはフィルタ)のサイズの枠(ウインドウ)を左上から右下へ順次スライドさせた範囲を対象に行われます。演算方法は、配列の各要素の積をとった後に要素の和を求めるというものです。以下に示した、動画を1から畳み込み演算を分解すると以下のようになります。
1) 左上[1 ,2, 4, 5] * [1, 1, 1, 1] = [1 * 1 + 2 * 1, 4 * 1, 5 * 1] = 12
2) 右上[2, 3, 5, 6] * [1, 1, 1, 1] = [2 * 1 + 3 * 1 + 5 * 1 + 6 * 1] = 16
3) 左下[4, 5, 7, 8] * [1, 1, 1, 1] = [4 * 1 + 5 * 1 + 7 * 1 + 8 * 1] = 24
4) 右下[5, 6, 8, 9] * [1, 1, 1, 1] = [5 * 1 + 6 * 1 + 8 * 1 + 9 * 1] = 28入力データ幅 : 3
入力データ高さ : 3
カーネル幅 : 2
カーネル高さ : 2
ストライド(詳細は後述します) : 1
2.1. ストライド
ストライドは、陸上競技の用語で歩幅を意味しますが、CNNではウインドウの移動幅を示す言葉として用いられます。次の例は、ストライドが1の場合の処理フローを表したもので、出力サイズが3x3になることがわかります。
入力データ幅 : 4
入力データ高さ : 4
カーネル幅 : 2
カーネル高さ : 2
ストライド : 1
続いて、入力サイズとカーネルサイズをそのままにして、ストライドを2にした場合の処理フローをみていきます。こちらは、最終的な結果が2x2となり、ストライドを1にした場合よりも縦横のサイズが1減っていることがわかります。 このようにCNNにおけるストライドとは、出力サイズを調整(減らす)する役割があります。入力画像が大きい場合など、効率的に処理する為に容量を圧縮できるという点で有効です。
入力データ幅 : 4
入力データ高さ : 4
カーネル幅 : 2
カーネル高さ : 2
ストライド : 2
2.2. パディング
ストライドは、出力サイズを小さくしたい時に使用しますが、逆に出力サイズを大きくしたい場合はパディングを使用します。以下の例のように入力データの周囲に0を埋めることで入力データサイズを増やします(0以外で埋めるパターンもあるようです)。入力データ(2x2)とカーネル(2x2)は何もしなければ出力サイズが1になりますが、パディングを行うと入力サイズが2x2から4x4になりますので、出力が1x1から3x3に増えます。
入力データ幅 : 2
入力データ高さ : 2
カーネル幅 : 2
カーネル高さ : 2
パディング : 1
2.2. 3次元データの畳み込み
カラー画像を扱う場合は、1ピクセルにRGB(Red, Green, Blue)の情報が含まれますので、縦横に加えて高さが必要になります。CNNでは、この高さをチャンネルもしくは深さ(Depth)と表現します。3次元の畳み込み演算では、このチャンネルに対してそれぞれカーネルを用意して演算を行います。そしてこれらの結果の総和を出力とします。
チャンネル : 3
入力データ幅 : 3
入力データ高さ : 3
カーネル幅 : 2
カーネル高さ : 2
パディング : 0
2.3. 4次元データの畳み込み
入力画像が複数ある場合は、4次元のデータを扱うことになります。この次元の単位をミニバッチと呼びます。3次元データの畳み込み演算ではチャンネル毎の畳み込み演算結果の和を求めましたが、4次元では、それぞれの結果が出力となる点に注意です。従って単純に、3次元データの畳み込みを入力画像数分行えば良いと考えれば良さそうです。
3. 実装
3.1. 2次元データの畳み込み
先に示した畳み込み演算の方法は、ウインドウの範囲の値とカーネルとの積をとって得た値の総和でした。実際の実装ではこの積和処理をより効率的に行う為に行列の積算問題として扱います。
行列の積算は、例えば4x4の行列を基準として列ベクトル(4x1)とすると以下のように求めることができます。

この処理の手順を列挙すると以下のようになります。ここで各行がウインドウで得た結果、(A,B,C,D)がカーネルだと想定し、2次元畳み込み処理の手順を振り返ってみてください。 各要素の積を取ったあとに和を求める工程が全く同じであることがわかります。
1) 1*A + 2*B + 3*C + 4*D <- 左上
2) 5*A + 6*B + 7*C + 8*D <- 右上
3) 9*A + 10*B + 11*C + 12*D <- 左下
4) 13*A + 14*B + 15*C + 16*D <- 右下つまりデータをこの形式にしてあげれば、ウインドウで得た配列とカーネルの積和の工程を毎回実行する必要は無く行列の積問題として一回で説くことができるということです。以下の例は、3x3の入力データと2x2のカーネルを入力した場合に行列と列ベクトルに整形する様子を表したものです。実際のプログラムでは、この考え方で実装していく方針とします。
では、まず入力画像から行列に展開する関数をim2colとして実装して行きます。また、これを実装するにあたってwindowクラスと、windowIteratorクラスを用意します。それぞれの役割は以下になります。
Im2col ・・・ 2次元のデータ(input)をウインドウに従って行列展開する関数
window・・・ 2次元のデータ(input)に対して 、現在どの範囲を対象にしているかを保持するクラス
windowIterator ・・・ウインドウを移動(イテレーション)するクラス
値を取得する範囲がwindow(ウインドウ)なので、Windowクラスは、以下のようにX軸の開始地点と終了地点、Y軸の開始地点と終了地点をメンバーとして保持します。
public class Window {
// 現在のX軸範囲
int startX;
int endX;
// 現在のY軸範囲
int startY;
int endY;
public Window(int startX, int endX, int startY, int endY) {
this.startX = startX;
this.endX = endX;
this.startY = startY;
this.endY = endY;
}
public Window(int width, int height) {
this.startX = 0;
this.endX = width;
this.startY = 0;
this.endY = height;
}
public int getStartX() {
return startX;
}
public int getEndX() {
return endX;
}
public int getStartY() {
return startY;
}
public int getEndY() {
return endY;
}
}次にWindowIteratorですが、こちらはWindowの移動をさせる役割を持ちます。 まずWindowの幅と高さをheightとwidthとして保持します。加えてWindowがX軸とY軸は最大どこまで動けるのかが必要なので、可動域としてmaxX, maxYを保持します。次にX軸とY軸は1回でどれだけ移動するのかの情報としてstrideXとstrideYを保持します。また、拡張for文でアクセスできるようにすると利用しやすいので、Iteratorインターフェースを実装させることにします。
WindowIteratorのメソッドは以下のようにhasNextとnextになります。
それぞれ、hasNextはWindowが終端まで行ったか?をboolで返却し、nextは、現状のウインドウの位置からストライド分を足し込んで次のウインドウを返却するという処理をしています。
public class WindowIterator implements Iterable<Window>, Iterator<Window> {
// 可動域
private final int maxX;
private final int maxY;
// Window幅&高さ
private final int width;
private final int height;
// 移動幅
private final int strideX;
private final int strideY;
// Window
private Window window;
public WindowIterator(int maxX, int maxY, int width, int height, int strideX, int strideY) {
this.maxX = maxX;
this.maxY = maxY;
this.width = width;
this.height = height;
this.strideX = strideX;
this.strideY = strideY;
}
public Iterator<Window> iterator() {
return this;
}
public boolean hasNext() {
if (this.window == null) {
return true;
}
if (isWindowEndOfX() && isWindowEndOfY()) {
return false;
}
return true;
}
public Window next() {
if (this.window == null) {
this.window = new Window(width, height);
return this.window;
}
if (!isWindowEndOfX()) {
Window window = new Window(
this.window.startX + strideX,
this.window.endX + strideX,
this.window.startY,
this.window.endY);
this.window = window;
return window;
} else {
Window window = new Window(
0,
this.width,
this.window.startY + strideY,
this.window.endY + strideY);
this.window = window;
return window;
}
}
public void remove() {
// do nothing
}
private boolean isWindowEndOfX() {
return this.window.endX == this.maxX;
}
private boolean isWindowEndOfY() {
return this.window.endY == this.maxY;
}
}次にこれらのWindowとWindowIteratorを使用して、im2colを実装します。大きく処理の流れは以下のようになります。
1) 入力(input)に対してパディングを行う(設計を考慮すると本来ここで処理すべきではないですが横着しました)
2) WindowIteratorでwindowを移動させinputからデータを取り出して結合する
3) 結合したデータを行列計算できるように整形(reshape)する
内部で行列に整形するため、ここではnd4jで行列操作を行うためのクラスであるINDArrayを引数と帰り値に適応しています。第2引数のConvolutionParameterは、入力サイズやカーネル、パディングの情報を保持するためのクラスです。出力サイズを取得するなど必要な振る舞いをカプセル化したいので切り出してあります。
public class ConvolutionParameter {
private int inputWidth;
private int inputHeight;
private int kernelWidth;
private int kernelHeight;
private int paddingWidth;
private int paddingHeight;
private int strideX;
private int strideY;
public static INDArray Im2col(INDArray input, ConvolutionParameter convolutionParameter) {
// もしPaddingの設定が1以上になっていれば、Paddingを行う
if (convolutionParameter.isPaddingAvailable()) {
int[][] padWidth = new int[][]{
{convolutionParameter.getPaddingHeight(), convolutionParameter.getPaddingHeight()},
{convolutionParameter.getPaddingWidth(), convolutionParameter.getPaddingWidth()}
};
input = Nd4j.pad(input, padWidth, Nd4j.PadMode.CONSTANT);
}
// WindowIteratorを生成します。
// Windowの横幅と高さは,Paddingを考慮したものを設定します。
WindowIterator iterator = new WindowIterator (
convolutionParameter.getInputWidthWithPadding(),
convolutionParameter.getInputHeightWithPadding(),
convolutionParameter.getKernelWidth(),
convolutionParameter.getKernelHeight(),
convolutionParameter.getStrideX(),
convolutionParameter.getStrideY()
);
// 入力(input)から現在のWindowのX軸の範囲とY軸の範囲を取得し、結合します。
INDArray result = null;
for (Window window : iterator) {
INDArray x = input.get(
NDArrayIndex.interval(window.getStartY(), window.getEndY()),
NDArrayIndex.interval(window.getStartX(), window.getEndX())
);
result = (result == null) ? x : Nd4j.concat(0, result, x);
}
// 出力数をrow, 一回の移動で取得する数をcolとして整形して返却します。
long rows = convolutionParameter.getOutputNum();
long cols = convolutionParameter.getKernelWidth() * convolutionParameter.getKernelHeight();
return result.reshape(rows, cols);
}
Nd4j.concat : INDArrayの結合が可能
NDArray.get : 指定したNDArrayIndexの値を取得することが可能
NDArray.reshape : 指定した行と列に変形することが可能
ここまでで、入力画像を行列に展開するまでの処理ができました。最後に2次元の畳み込み処理を行う関数を実装します。
第一引数は、INDArrayの2次元データをinputとし、第二引数はINDArrayの2次元データをカーネルとして受け取ります。また、第3引数は各種パラメータです。
public static INDArray Convolution2D(INDArray input, INDArray kernel, ConvolutionParameter parameter) {
INDArray arr = Im2col(input, parameter);
INDArray reshaped = kernel.reshape(parameter.getKernelHeight() * parameter.getKernelWidth(), 1);
INDArray convolved = arr.mmul(reshaped);
return convolved.reshape(new int[]{parameter.getOutputWidth(), parameter.getOutputHeight()});
}まずは入力データinputを行列展開します。次にカーネルを列ベクトルに展開します。これをmmul関数で行列*列ベクトルの計算を行い、最終的にでた結果に対して整形を行います。呼び出しは以下のようになります。
{
int height = 3;
int width = 3;
int kH = 2;
int kW = 2;
int sX = 1;
int sY = 1;
int pX = 0;
int pY = 0;
ConvolutionParameter parameter = new ConvolutionParameter(height, width, kH, kW, pY, pX, sX, sY);
// kernel
// kernel patternA
INDArray kernel = Nd4j.create(new double[][]{
{1, 1},
{1, 1}
});
//Input data: shape [miniBatch,depth,height,width]
INDArray input = Nd4j.create(new double[][]{
{1, 2, 3},
{4, 5, 6},
{7, 8, 9}
});
INDArray result = ConvolutionUtil.Convolution2D(input, kernel, parameter);
INDArray expected = Nd4j.create(new double[][]{
{12, 16},
{24, 28}
});
assertEquals(expected, result);
}
3.2. 3次元データの畳み込み演算
行列演算を利用して2次元の畳み込み演算を行ました。次に3次元データに対して、考えてみます。3次元データは、各チャンネルの計算結果を足しこむことで出力を得られるということを思い出してください。つまり、各チャンネルの行列展開した結果を結合して行列計算してしまえば良いということです。以下は、3次元データを結合する処理フローを表したものです。
この処理を実装に起こすと以下のようになります。2次元の畳み込みと時と同じようにinput,kernel, convolutionParameterを受け取ります。convolution3dではこれに加えてチャンネル数(depth)を受け取ります。
このdepth数分forでループして、それぞれのチャンネルの行列展開した結果及びカーネルの列ベクトルをマージします。最後にmmulで行列の積演算を行い出力を整形するという処理になっています。
public static INDArray Convolution3D(INDArray input, INDArray kernel, int depth, ConvolutionParameter parameter) {
INDArray inputMerged = null;
INDArray kernelMerged = null;
for (int i = 0; i < depth; i++) {
INDArray arr = Im2col(input.get(new INDArrayIndex[]{point(i)}), parameter);
inputMerged = (inputMerged == null) ? arr : Nd4j.concat(1, inputMerged, arr);
INDArray ker = kernel.get(new INDArrayIndex[]{point(i)});
INDArray reshapedKer = ker.reshape(parameter.getKernelHeight() * parameter.getKernelWidth(), 1);
kernelMerged = (kernelMerged == null) ? reshapedKer : Nd4j.concat(0, kernelMerged, reshapedKer);
}
INDArray convolved = inputMerged.mmul(kernelMerged);
return convolved.reshape(new int[]{parameter.getOutputWidth(), parameter.getOutputHeight()});
}
convolution3Dの呼び出し方は以下のようになります。
int height = 3;
int width = 3;
int kH = 2;
int kW = 2;
int sX = 1;
int sY = 1;
int pX = 0;
int pY = 0;
int depth = 2;
ConvolutionParameter parameter = new ConvolutionParameter(height, width, kH, kW, pY, pX, sX, sY);
// kernel
// kernel patternA
INDArray kernel = Nd4j.create(new double[][][]{
{
{1, 2},
{3, 4}
},
{
{5, 6},
{7, 8}
},
});
//Input data: shape [miniBatch,depth,height,width]
INDArray input = Nd4j.create(new double[][][]{
{
{1, 2, 3},
{4, 5, 6},
{7, 8, 9}
},
{
{1, 2, 3},
{4, 5, 6},
{7, 8, 9}
}
});
INDArray result = ConvolutionUtil.Convolution3D(input, kernel, depth, parameter);
INDArray expected = Nd4j.create(new double[][]{
{122, 158},
{230, 266}
});
assertEquals(expected, result);
3.3. 4次元データの畳み込み演算
4次元データの畳み込みは3次元のメソッドのパラメータに加えてバッチ数(miniBatch)を入力します。3次元のようにマージして一発で取得したいところなんですが、別々に積和演算する必要があるので愚直にconvolution3dを呼び出す実装としてます。
public static INDArray Convolution4D(INDArray input, INDArray kernel, int miniBatch, int depth, ConvolutionParameter parameter) {
INDArray result = Nd4j.create(new int[]{miniBatch, parameter.getOutputWidth(), parameter.getOutputHeight()}, 'c');
for (int i = 0; i < miniBatch; i++) {
INDArray input3D = input.get(new INDArrayIndex[]{point(i)});
INDArray kernel3D = kernel.get(new INDArrayIndex[]{point(i)});
INDArray convolved = Convolution3D(input3D, kernel3D, depth, parameter);
result.put(new INDArrayIndex[]{point(i), all(), all()}, convolved);
}
return result;
}ここまでの実装は、全てここにおいてあるので気になる方は見てみてください。例外処理したり設計を見直したり、機能追加したりするのも面白いかもしれません。
4. まとめ
CNNの畳み込み処理についてまとめました。
ニューラルネットワークについては勉強中なので、もし間違いなどありましたらご指摘いただけると幸いです。
