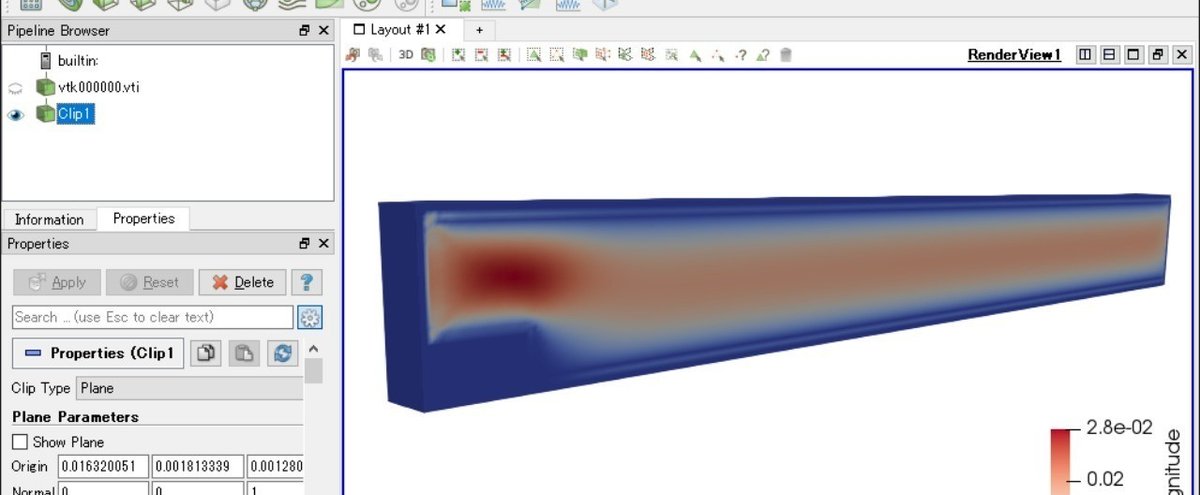
格子ボルツマン法オープンソ―スPalabosを使って手持ちのSTLで計算してみた
前回はコードをPalabosについてザックリと中身を見てみました。今回は手持ちのSTLファイルを使用して任意形状に対する流れの計算が行えれるか調査してみました
目次
・Palabosについて
・Palabosのコード
・今回の調査内容
・STLを使った計算の調査
・STLを使った算の調査(今回の調査内容)
・STLを使った例題
・STL差し替え時の注意点
・結果の確認
・コードの改造
・領域全体の結果を追加する
・writeVtkの移植
・writeVtkの書き換え
・writeVtkの呼び出し
・計算の実行
・結果の確認①
・結果の確認②
・今後の目標
Palabosについて
格子ボルツマン法ソルバを書くためのライブラリです。開発元はNUMECA社と共同で商用の格子ボルツマン法ソフトを開発しています。基本的にGUIとかはなく、コードを書いてソルバを作るタイプのオープンソースのため、少し難易度は高いです。
Palabosのコード
Palabosのコードの例を次に示します。PalabosのコードはC++で記述します。Palabosはソルバを作る上で必要となる機能をクラスや関数で提供しているため、開発者はそれらを利用することでソルバ開発を比較的簡単に書くことができます。
...
#include "palabos2D.h"
#include "palabos2D.hh"
#include <iostream>
#include <iomanip>
using namespace plb;
using namespace std;
typedef double T;
#define DESCRIPTOR plb::descriptors::D2Q9Descriptor
// Initialize the lattice at zero velocity and constant density, except
// for a slight density excess on a square sub-domain.
void defineInitialDensityAtCenter(MultiBlockLattice2D<T,DESCRIPTOR>& lattice)
{
// The lattice is of size nx-by-ny
const plint nx = lattice.getNx();
const plint ny = lattice.getNy();
// Create a Box2D which describes the location of cells with a slightly
// higher density.
plint centralSquareRadius = nx/6;
plint centerX = nx/3;
plint centerY = ny/4;
Box2D centralSquare (
centerX - centralSquareRadius, centerX + centralSquareRadius,
centerY - centralSquareRadius, centerY + centralSquareRadius );
// All cells have initially density rho ...
T rho0 = 1.;
// .. except for those in the box "centralSquare" which have density
// rho+deltaRho
T deltaRho = 1.e-4;
Array<T,2> u0((T)0,(T)0);
// Initialize constant density everywhere.
initializeAtEquilibrium (
lattice, lattice.getBoundingBox(), rho0, u0 );
// And slightly higher density in the central box.
initializeAtEquilibrium (
lattice, centralSquare, rho0 + deltaRho, u0 );
lattice.initialize();
}
int main(int argc, char* argv[]) {
plbInit(&argc, &argv);
global::directories().setOutputDir("./tmp/");
const plint maxIter = 1000; // Iterate during 1000 steps.
const plint nx = 600; // Choice of lattice dimensions.
const plint ny = 600;
const T omega = 1.; // Choice of the relaxation parameter
MultiBlockLattice2D<T, DESCRIPTOR> lattice (
nx, ny, new BGKdynamics<T,DESCRIPTOR>(omega) );
lattice.periodicity().toggleAll(true); // Use periodic boundaries.
defineInitialDensityAtCenter(lattice);
// Main loop over time iterations.
for (plint iT=0; iT<maxIter; ++iT) {
if (iT%40==0) { // Write an image every 40th time step.
pcout << "Writing GIF file at iT=" << iT << endl;
// Instantiate an image writer with the color map "leeloo".
ImageWriter<T> imageWriter("leeloo");
// Write a GIF file with colors rescaled to the range of values
// in the matrix
imageWriter.writeScaledGif (
createFileName("u", iT, 6),
*computeVelocityNorm(lattice) );
}
// Execute lattice Boltzmann iteration.
lattice.collideAndStream();
}
}今回の調査内容
STLを使った計算の調査
そもそもPalabosは形状定義用のクラスなども内包しており、基本形状(矩形、円、立方体、球など)は寸法を指定することで作成できます。ですが、実用的な計算ではこれら基本形状だけではモデルを作ることができないことも多いため、CADデータなどで作成した任意形状に対して計算できる機能が必要になります。
前回の調査で3次元モデルデータの形式のひとつであるSTLファイルを使用した例題があることが分かっておりますので、まずはその例題を見ていこうと思います。
STLを使った例題
STLを使用した例題はPalabosのフォルダにディレクトリ内にある次の場所にありました。
example/showcase/aneurysm
これは動脈瘤の計算事例のようで、内部流れの事例となっているようです。
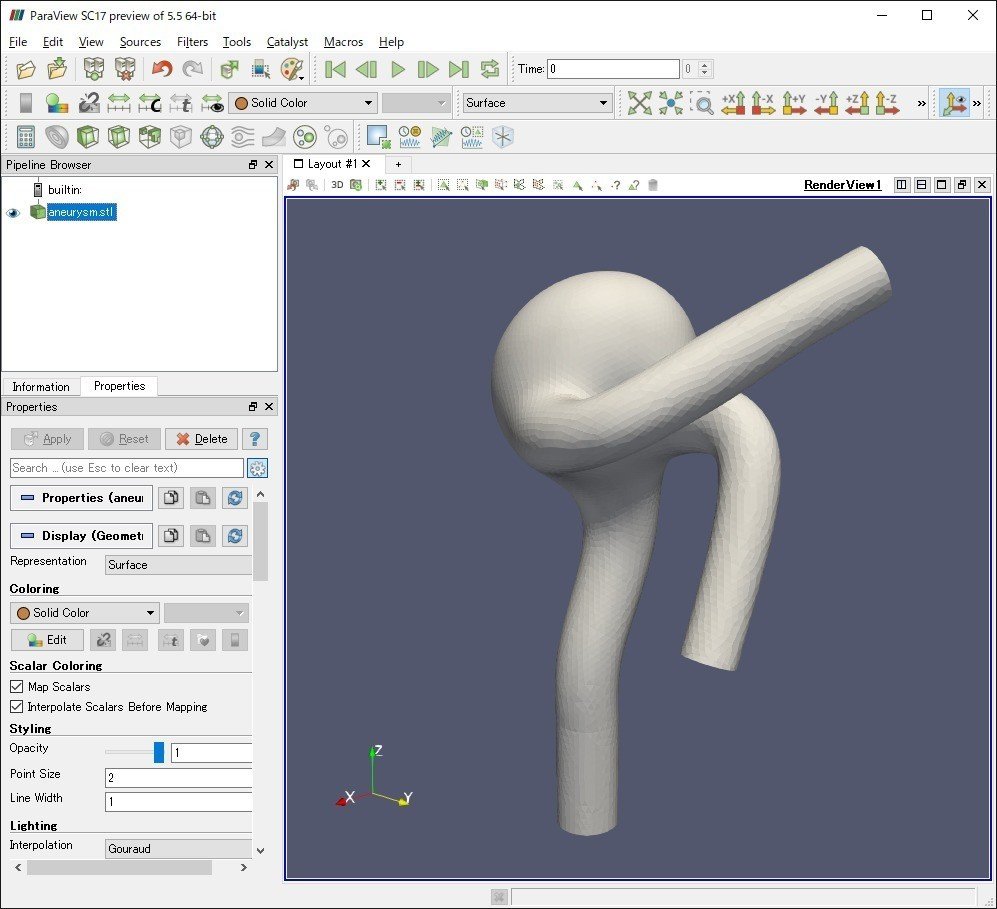
この例題はインプットファイルでSTLファイルを指定しているので、とりあえずSTLのファイル名を差し替えてみます。差し替えるのはオープンCAE勉強会@関西でおなじみのバックステップ流れのSTLファイルです。
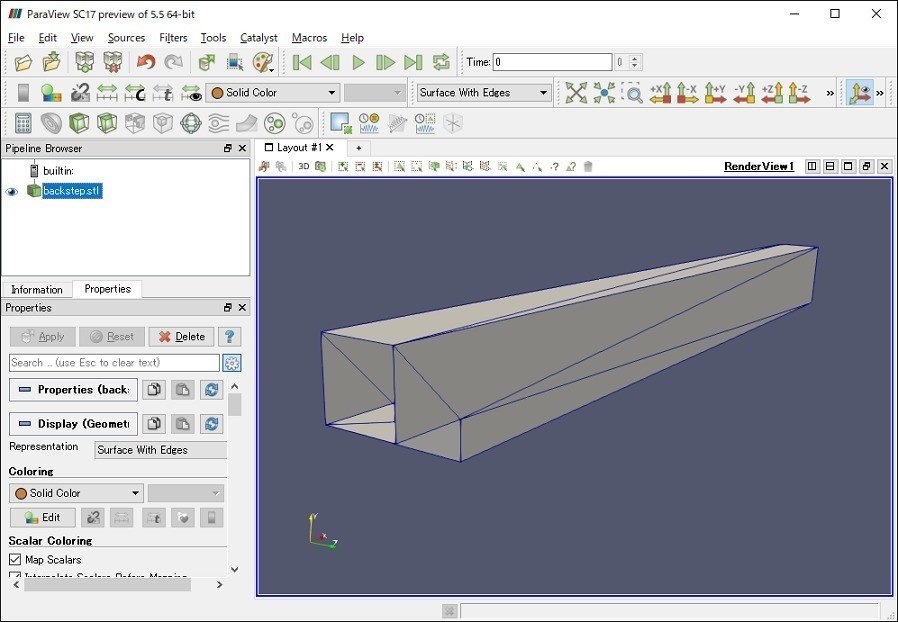
例題フォルダの中にあるparam.xmlがソルバのインプットファイルとなっており、STLファイルを中で指定しているので書き換えます。また、このファイルには流入速度なども書いてあるので、適宜変更します。
<?xml version="1.0" ?>
<geometry>
<mesh> ./backstep.stl </mesh>
...STL差し替え時の注意点
aneurysmの例題ではSTLファイルのモデルに作成上の注意点があります。流入、流出となる面はstl上で開口としておく(面を作らない)必要があります。下の図では流入面から見て、奥の流出面の向こう側の背景まで見えていますが、面の表示を消しているわけでなく、モデルデータ上で面自体を消しています。
aneurysmの例題ではSTLの穴が開いているところを流入出面として判定します。
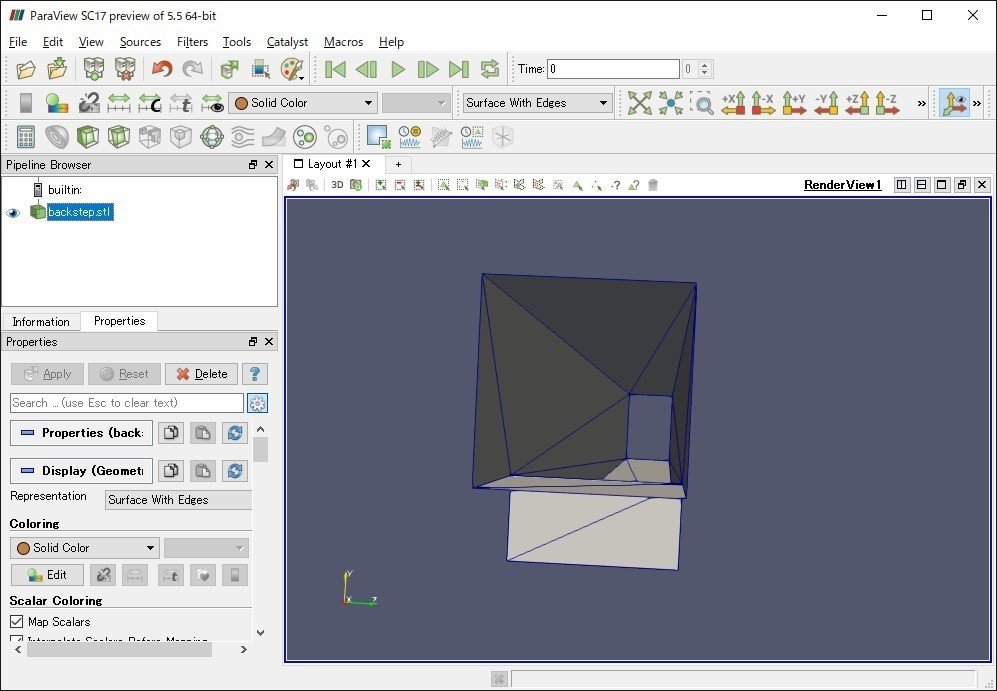
コードの書き換えが終わったらコンパイルして実行します。
make >Make_2.log 2>&1
./backstep param.xml結果の確認
aneurysmの例題では可視化ソフトのParaviewで表示できるvtkファイルが出力されるので、Paraviewを使用して結果を確認します。Paraviewはオープンソースの可視化ソフトのため、だれでも利用は無償で行えます。
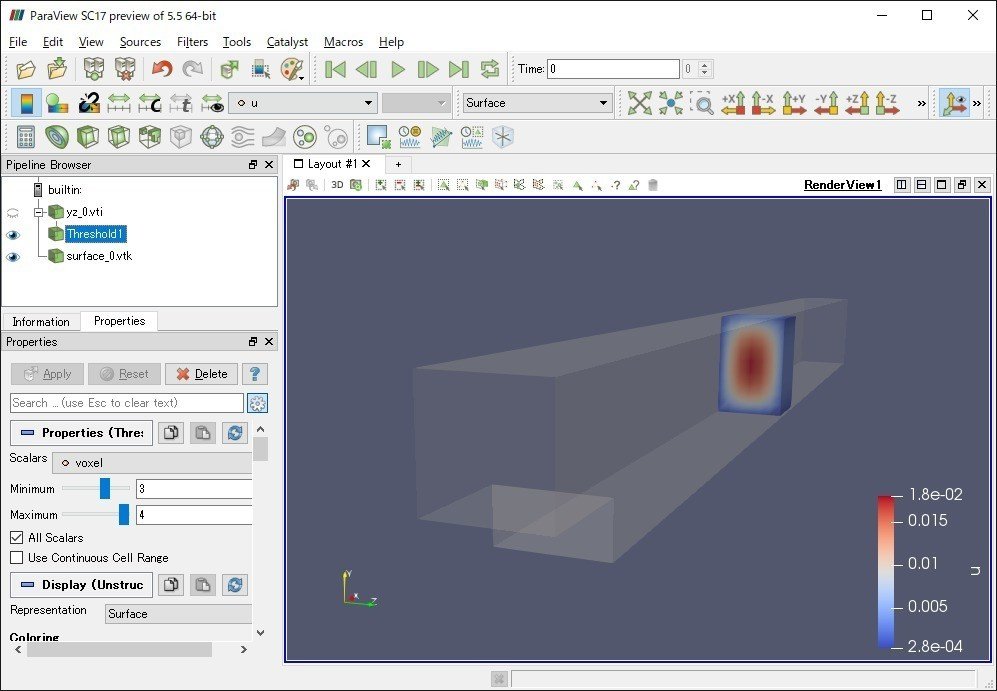
結果を確認すると、とりあえず計算できていることがわかりました。汎用性の高い例題コードであることがわかります。
ただ元のaneurysmの例題が特定領域を切り出した結果を出しているので、STLファイルの領域すべてに対する結果は出て来ておりません。また、流速のベクトル結果も出てきておりませんでした。
次はコードを改造して領域すべての結果の出力とベクトル結果の出力ができるようにしていきます。
コードの改造
結果を追加する
領域結果の出力とベクトル結果の出力を加えます。とはいえ何もないところからコードを改造するのはハードルが高いので、まずはベクトル結果を出力している例題のコードを探します。
exampleの中のコードを一つづつ見ているとcavity3dのケースが使えそうなことがわかりました。cavity3dのコードを読み、領域結果を出力しているwriteVtk関数をaneurysmの例題コードに移植することにしました。
...
template<class BlockLatticeT>
void writeVTK(BlockLatticeT& lattice,
IncomprFlowParam<T> const& parameters, plint iter)
{
T dx = parameters.getDeltaX();
T dt = parameters.getDeltaT();
//VtkImageOutput3D<T> vtkOut(createFileName("vtk", iter, 6), dx);
ParallelVtkImageOutput3D<T> vtkOut(createFileName("vtk", iter, 6), 3, dx);
vtkOut.writeData<3,float>(*computeVelocity(lattice), "velocity", dx/dt);
vtkOut.writeData<float>(*computeVelocityNorm(lattice), "velocityNorm", dx/dt);
vtkOut.writeData<3,float>(*computeVorticity(*computeVelocity(lattice)), "vorticity", 1./dt);
}
...writeVtk関数の中身はとりあえず見ないことにします。
writeVtkの移植
writeVtkを移植していきますが、aneurysmの例題コードの中にある似たようなwriteImage関数の近くにコピペしました。aneurysmの例題ではwriteVtk関数内のiterは定義していないので、適当に0とかを入れて定義しました。
...
template<class BlockLatticeT>
void writeVTK(BlockLatticeT& lattice,
IncomprFlowParam<T> const& parameters, plint iter)
{
T dx = parameters.getDeltaX();
T dt = parameters.getDeltaT();
int iter = 0;
//VtkImageOutput3D<T> vtkOut(createFileName("vtk", iter, 6), dx);
ParallelVtkImageOutput3D<T> vtkOut(createFileName("vtk", iter, 6), 3, dx);
vtkOut.writeData<3,float>(*computeVelocity(lattice), "velocity", dx/dt);
vtkOut.writeData<float>(*computeVelocityNorm(lattice), "velocityNorm", dx/dt);
vtkOut.writeData<3,float>(*computeVorticity(*computeVelocity(lattice)), "vorticity", 1./dt);
}
...writeVtkの書き換え
writeVtkはcavity3d用なので、引数などをaneurysmの例題コードに対応するように書き換えます。ここはコンパイルとエラーメッセージを見ながらごり押しで作業しました。
...
template<class BlockLatticeT>
void writeVTK(BlockLatticeT& lattice,
T dx, T dt)
{
//T dx = parameters.getDeltaX();
//T dt = parameters.getDeltaT();
int iter = 0;
//VtkImageOutput3D<T> vtkOut(createFileName("vtk", iter, 6), dx);
ParallelVtkImageOutput3D<T> vtkOut(createFileName("vtk", iter, 6), 3, dx);
vtkOut.writeData<3,float>(*computeVelocity(lattice), "velocity", dx/dt);
vtkOut.writeData<float>(*computeVelocityNorm(lattice), "velocityNorm", dx/dt);
vtkOut.writeData<3,float>(*computeVorticity(*computeVelocity(lattice)), "vorticity", 1./dt);
}
...writeVtkの呼び出し
writeVtkを呼び出す場所はwriteImageの近くに置きました。
...
// Image output.
if (doImages) {
writeImages(boundaryCondition, level, location, dx, dt);
...
// Add
writeVTK(*lattice, dx, dt);
// -----
}
...計算の実行
改造が終わったのでコンパイルして実行します。
make >Make_2.log 2>&1
./backstep param.xml結果の確認①
計算の実行後、新たにvtkファイルが一つできたので、Paraviewで確認します。計算領域全体の流速コンタが描けました。
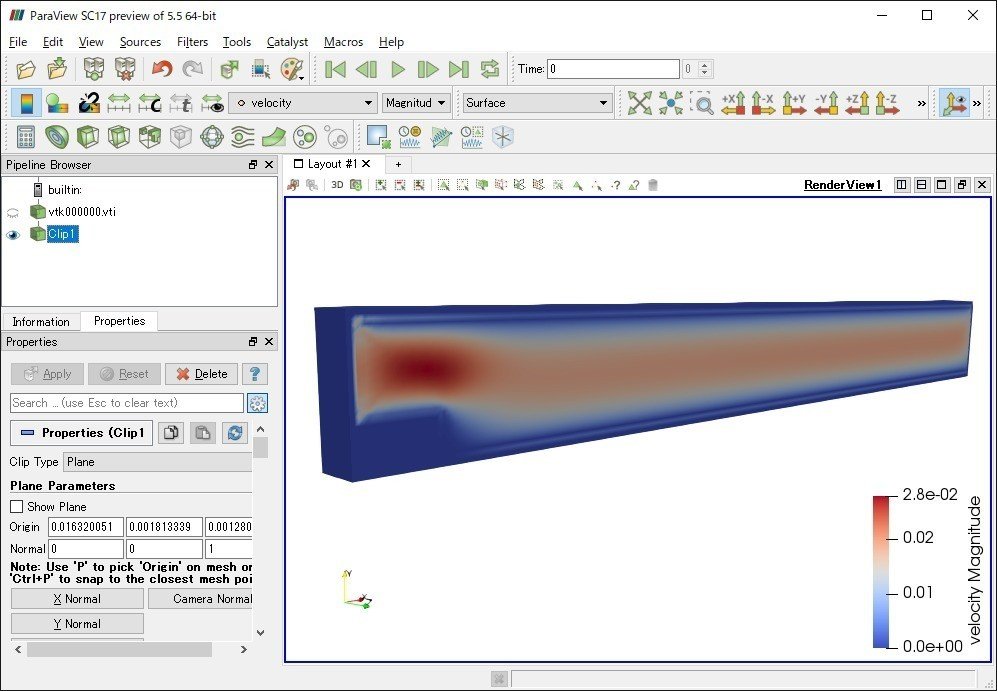
結果の確認②
流線が描けました。ベクトルデータも出力できているようです。
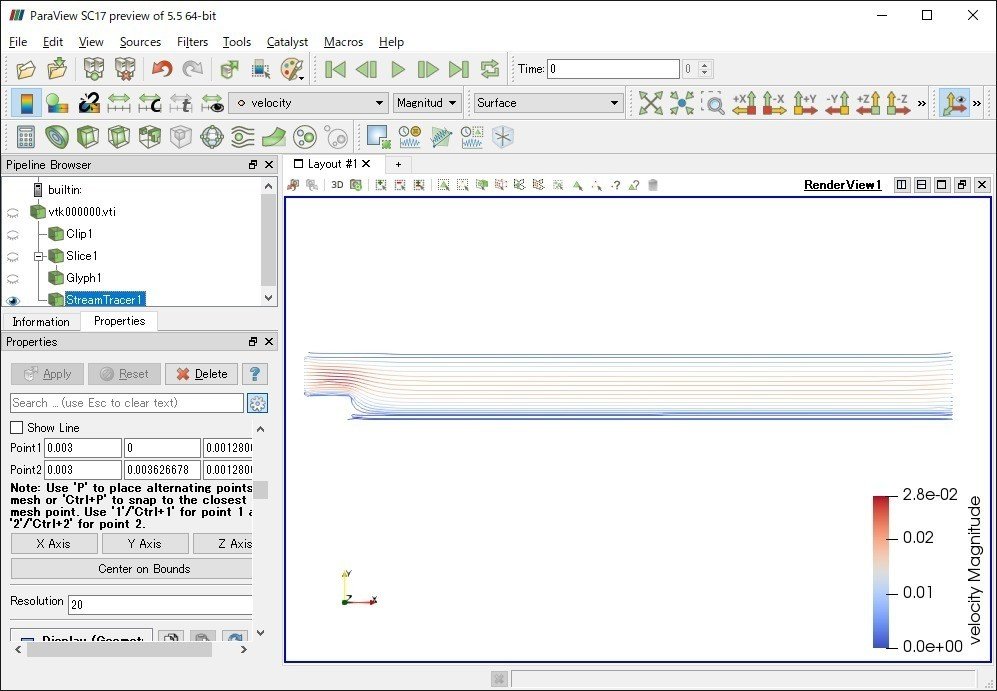
今後の目標
領域全体の結果を出力できるようにコードの書き換えができましたが、計算領域の不要な部分、つまりSTLファイルで定義した外側の領域の結果まで表示されていました。実務の計算において不要な領域の結果は時としていらぬ誤解を招くため、できれば表示したくないものです。そのため計算ソルバでは一般的に、こうした領域内外を判定する変数が、結果と出力されます。
Palabosでこれを実現するにはaneurysmの例題で出力されているvoxel変数の出力が必要になります。voxel変数はSTLファイルの内部と外部を判別するためのフラグ変数となっており、下の図のようにvoxel変数を使ってSTLの内部領域だけの表示ができるようになります。
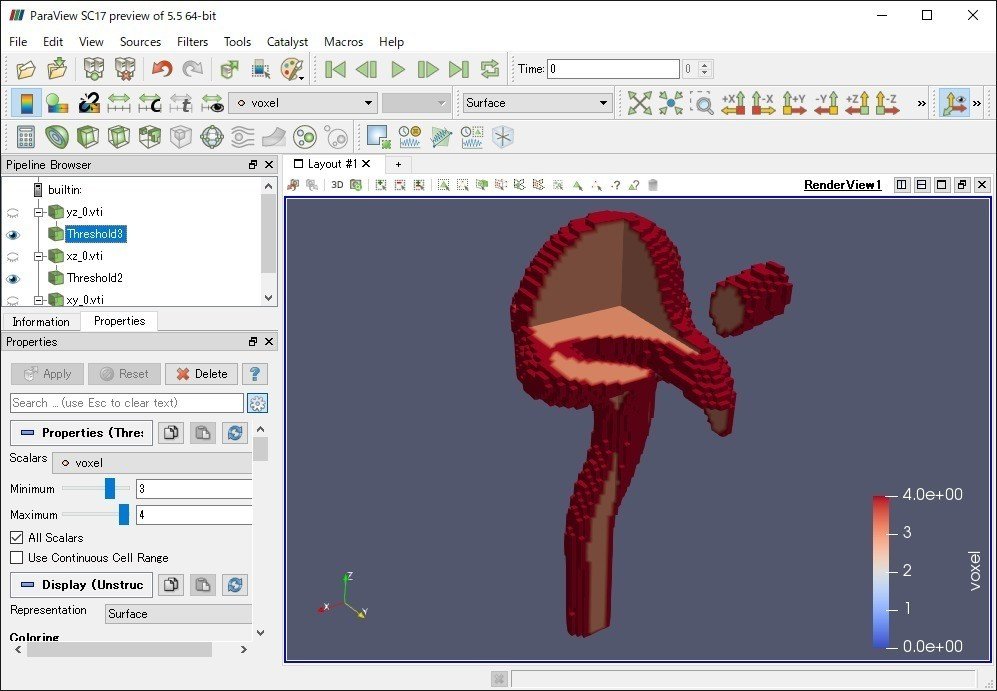
ただし、aneurysmの例題ではモデル全体のvoxel変数は出力されていません。今回移植したwriteVtk関数を改造してvoxel変数を出力できるようにすればSTLファイルの内部領域だけを表示してコンタを書けそうです。
今後はvoxel変数の出力にトライしていきます。
