努力と成長に関する数学的考察 その１

※この連載では、無駄に数式が登場します。数式アレルギーをお持ちの方は、読むのをお控えください。

突然ですが、シグモイド曲線と呼ばれるような、S字型の曲線があります。

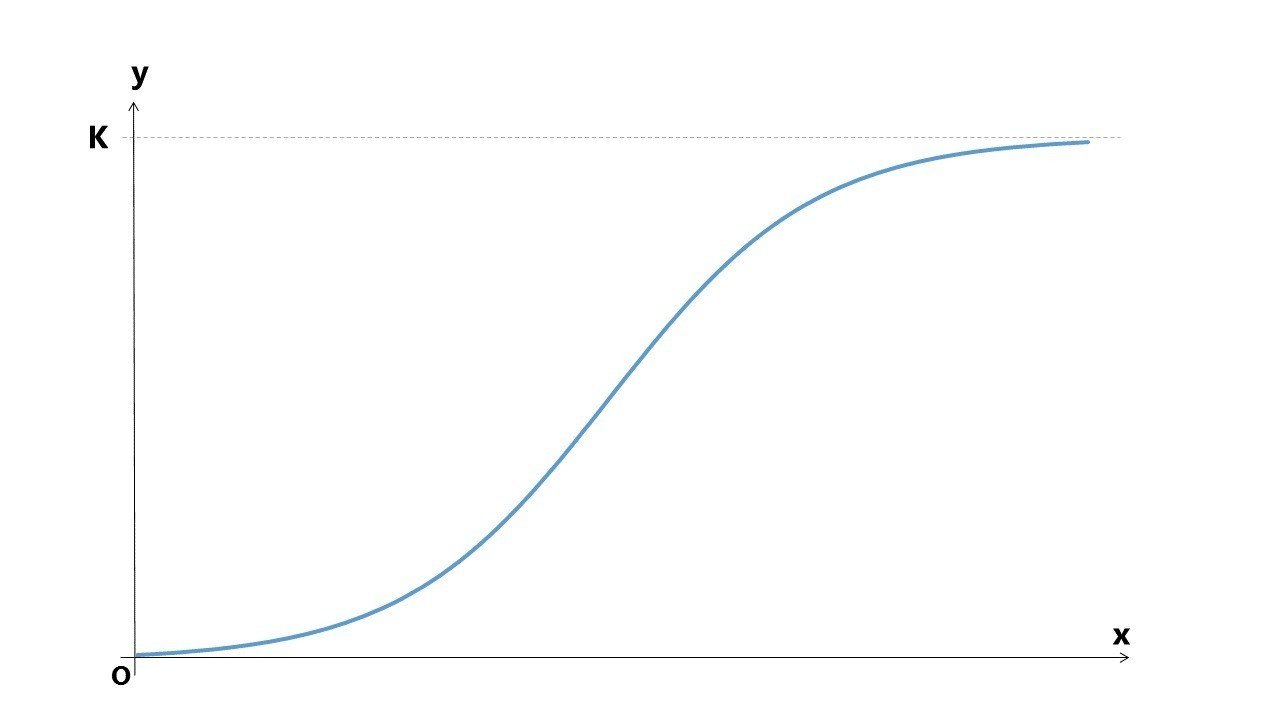
有名なシグモイド曲線の１つである、ロジスティック曲線を例に考えてみましょう。
y=0 と y=K の２本の直線を漸近線に持つような、単調増加のS字曲線です。

増殖曲線とも呼ばれるように、生物の個体数の増加をモデルにして導くことができます。

ある時刻 t における個体数 Y の増加率 dY/dt は、その時点での Y に比例すると考えます。

dY/dt ＝ rY　(r>0)

しかし Y は、現実の世界においては何らかの制約の影響を受けるため、無限に増殖できるわけではありません。
その環境が許容できる Y の最大値を K(>0) とすれば、Y が K に近付くにつれ、Y の増加率は低下します。

dY/dt ＝ rY(1−Y/K)

Y→K のときの、dY/dt の極限は 0 です。 

この微分方程式を、ロジスティック方程式と呼びます。

変数分離可能な微分方程式なので、比較的簡単に解くことができます。
Y について解くと、次式のようになります（Cは定数）。

Y ＝ K/{1＋exp(−rt−C)}

ゼロまたはマイナスの個体数から生物が増加することはないため、基本的には Y(0)>0 となるような初期値を取ります。
この最初の個体がニワトリなのか卵なのかは、僕は知りません。

Y(0)=P>0 として、C について解くと、以下のようになります。

C ＝ −log{(K−P)/P}

したがって、

exp(−C) ＝ (K−P)/P

であり、これを α と置くと、Y は以下のように表すことができます。

Y ＝ K/{1＋α exp(−rt)}

この式が、ロジスティック関数です。

では、今度は努力と成長の関係を考えてみましょう。

生物個体数の増加モデルの場合、K がその環境が許容できる個体数ポテンシャルの限界であり、r は増加率を決める係数、α は限界値 K と初期値 P によって定められる定数です。

では、成長度 y が、努力量 x の関数であると仮定した場合はどうでしょうか。
初期値 P は、生まれつきの能力値ですから、才能とでも定義しておきましょう。

r は成長率を決める係数です。
K は、その人（ないしはチーム）が、その環境で、そのやり方で到達し得る成長の最大値であります。

通常、成長は努力に単純比例すると思いがちですが、実際には、努力をしていてもしばらくはなかなか成長しません。
人間の思考の線形性と現実世界の非線形、ここに理想と現実のギャップが生まれます。

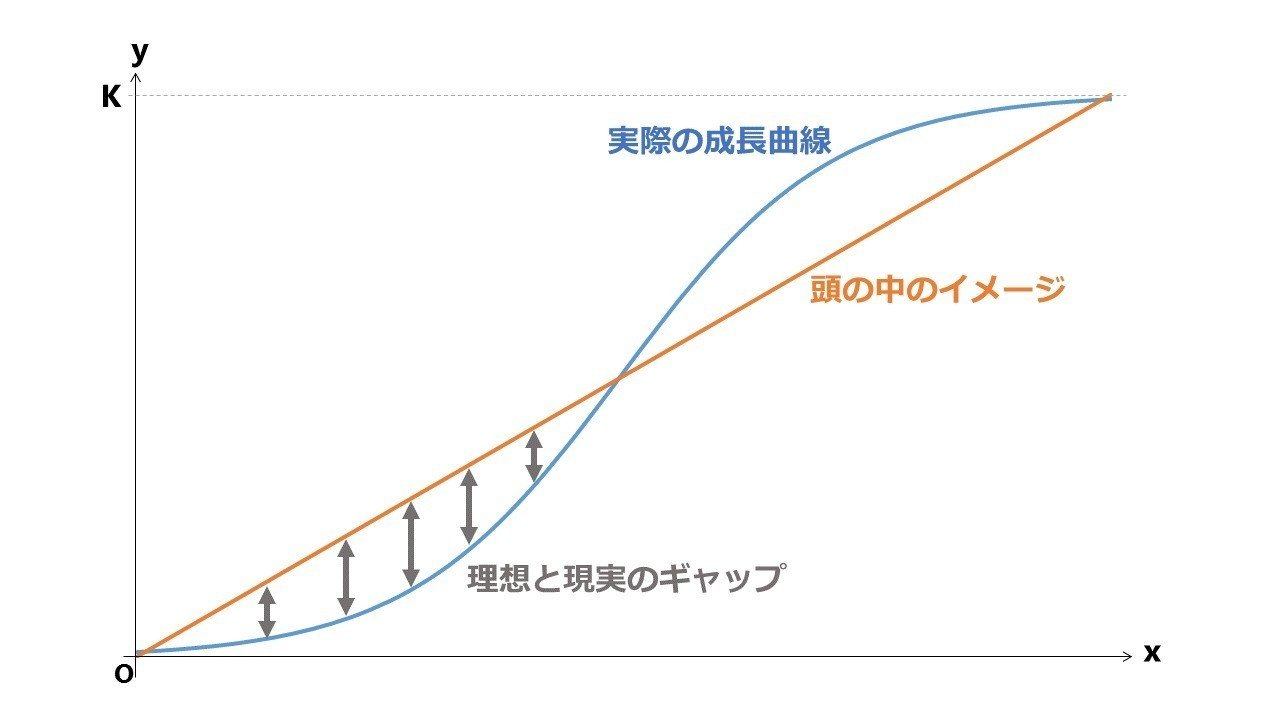
頭の中では直線的に成長すると信じ込んでいる場合、努力をしてもしばらく成果が出ないため、何かしら理由をつけて、図の前半の段階で諦めてしまいがちです。

これは、あらゆるケースで同じことが言えます。
受験勉強、スポーツ、新商品の売上、ブランドの認知度、テクノロジーの普及、etc。

このことからまずはじめに言いたいのが、成果が出始める前の初期段階で「成長しない」と決めつけて諦めてはいけないということ。

とはいえ、これだけの浅い精神論のためだけなら、わざわざ数式を持ち出すまでもありませんね。

次回、もう少し深く考えてみます。