FIRフィルタ
FIRフィルタが何をしているか,どう作れるか,諸現象の原因は何かなどをまとめました。とは言ってもPA現場レベルで必要になることはないと思いますが,FIRフィルタの普及に伴い理解が必要になる時が来るかもしれないくらいのつもりで書いてます。畳み込み,フーリエ変換をなんとなく理解している人に対してFIRフィルタの少し踏み込んだところを解説する目的で記述しています。かなり乱暴な記載も多いので,より詳細,正確な知識を求めている方は参考文献をご参照ください。
FIRフィルタとIIRフィルタ
Finite Impulse Response(有限インパルス応答)フィルタの頭文字をとってFIRフィルタです。非巡回型(フィードバックしていない)のフィルタです。対になる概念はInfinite Impulse Response(無限インパルス応答)フィルタ,通称IIRフィルタです。こちらはフィードバックを利用して所望の特性を実現します。
歴史的にはIIRフィルタの方が長く,これはIIRフィルタが回路によって(アナログに)容易に実現できたからです。アナログフィルタの設計手法は制御理論の文脈で高度に発展しており,これはこれで非常に有用です。最新のデジタル機器内に搭載されているIIRディジタルフィルタは,アナログフィルタを変換して(数式を変形してデジタルに落とし込む)実現しています。
一方FIRフィルタはディジタル信号処理の隆盛,つまり計算機と共に圧倒的に進化していきます。IIRフィルタには魅力的な点も多くありますが,非直線形位相という犠牲のもとで優れた振幅特性を得ているのが普通です。一方FIRフィルタは原理上正確に直線位相にすることができます。(しないこともできます)この直線位相であることのメリット,デメリットも含め以降では議論していきます。
FIRフィルタと畳み込み
FIRフィルタを音声信号へ作用させるためには時間領域で畳み込み(Convolution)を行います。つまりFIRフィルタという名の任意のインパルス応答を音声信号に畳み込むことで音声信号へのフィルタリングが行えます。そういう意味ではコンボリューションリバーブも立派なFIRフィルタです。
しかしこの畳み込みはそのまま馬鹿正直にやろうとすると計算量がものすごいことになります。さて,時間領域の畳み込みは,周波数領域では単なる乗算になること(畳み込み定理)が知られています。そのため一般的に畳み込みは等価な計算としてFFT(高速フーリエ変換)を行なって周波数領域で乗算し,IFFT(逆高速フーリエ変換)して時間領域に戻す手法*がよく用いられています。
また長時間の音声信号では音声信号を一定のブロックに区切って処理を行うOverlap-Add法やOverlap-Save法が,ライブのようなリアルタイムで逐次入力されてくる音声信号に対してはSTFT(短時間フーリエ変換)によって逐次処理を行うことが一般的かと思います。
*これはFFT(高速フーリエ変換)がDFT(離散フーリエ変換)を圧倒的に速く計算できるからこそ成り立つ手法です。DFTだけでは計算量がそれなりに大きいですが,FFTの発明により気軽に周波数領域で物事を見たり計算したりができるようになりました。音響研究をしている人は息を吸うようにFFTを行います笑
FIRフィルタの設計
FIRフィルタにはいくつか設計方法があります。といっても,いくつか挙げても読みにくいので,今回は周波数領域で設計する方法を紹介します。
周波数領域での設計の概要
以下の図にある関係を知っていることが前提となります。インパルス応答をフーリエ変換すると伝達関数になり,伝達関数を逆フーリエ変換するとインパルス応答になります。
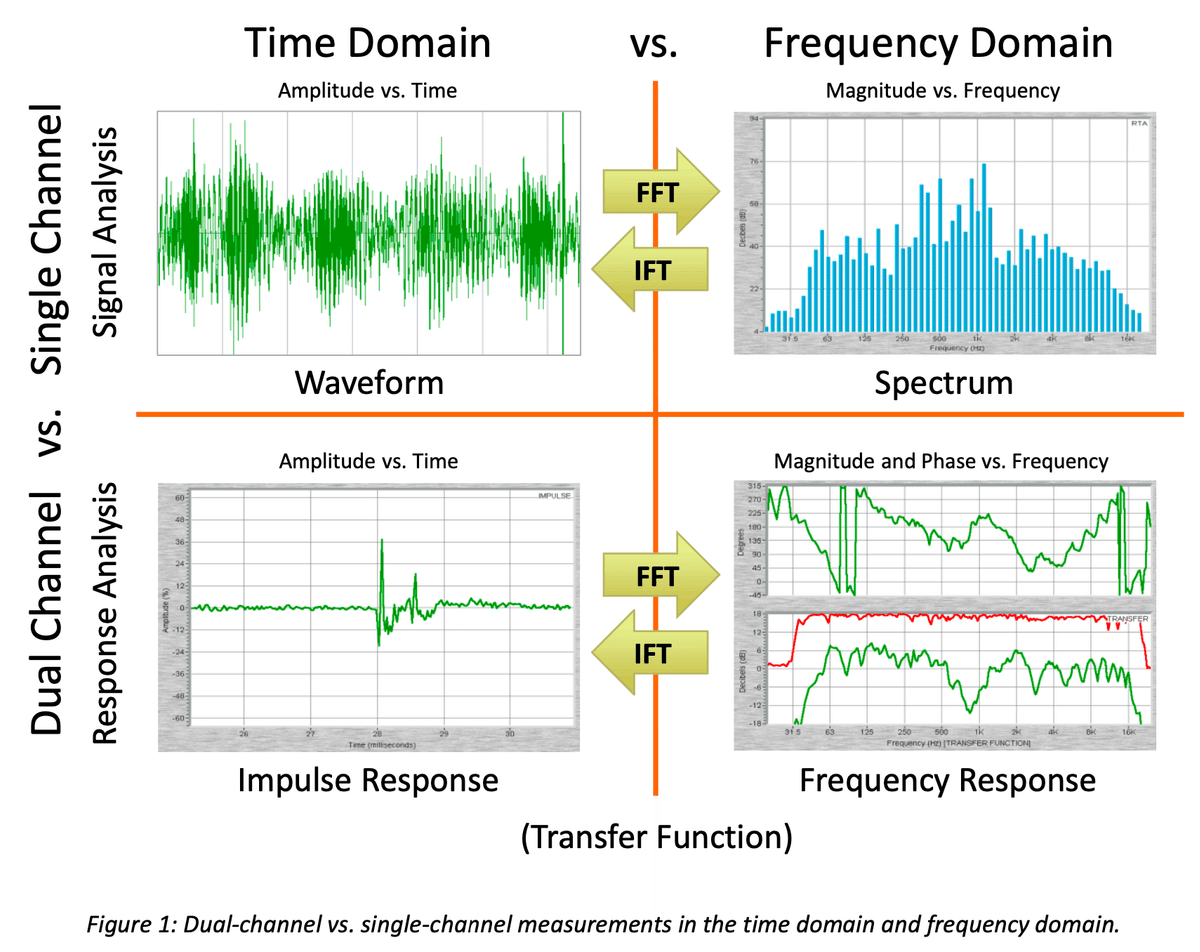
インパルス応答はLTI(線形時不変)システムで特に重要な概念です。
有限長の数列(音声信号もデジタルにしてしまえば単なる時系列の数列です)はその離散フーリエ変換で表せることを利用し,周波数領域で所望の特性を作成し,離散逆フーリエ変換によってFIRを得るやり方です。つまりFIRフィルタを設計するにあたって,直接インパルス応答を作るわけではなく,伝達関数を設計してから逆フーリエ変換によってFIRを得ます。
イメージとしてはSmaartのTF画面にあるようなMaginitudeで欲しい振幅特性を作成して,それをIFFTすることで有限長のインパルス応答を得るといった感じです(位相特性を指定しない場合線形位相特性となります)。要はタップ数を十分に取って所望特性を周波数領域で好きなように作ってしまえるわけで,これこそがFIRフィルタの自由度の高さですね。
線形位相FIRフィルタの設計例
それでは例を示します。1000 Hzを中心にcosineカーブで-3 dBするpeaking filterを所望特性とします。この時位相特性は指定せずに,振幅特性のみを実数値数列で与える(これは線形位相特性を指定してることと等価ですが)とします。

実際はdBではなく真数で設計が必要
これを逆フーリエ変換して時間領域にする(インパルス応答にする)と以下の図のようになります。(今回はpythonの科学技術計算用ライブラリであるscipyのfft.irfft 1.10.0を使用しています。本来は負の周波数まで考慮する必要があります)
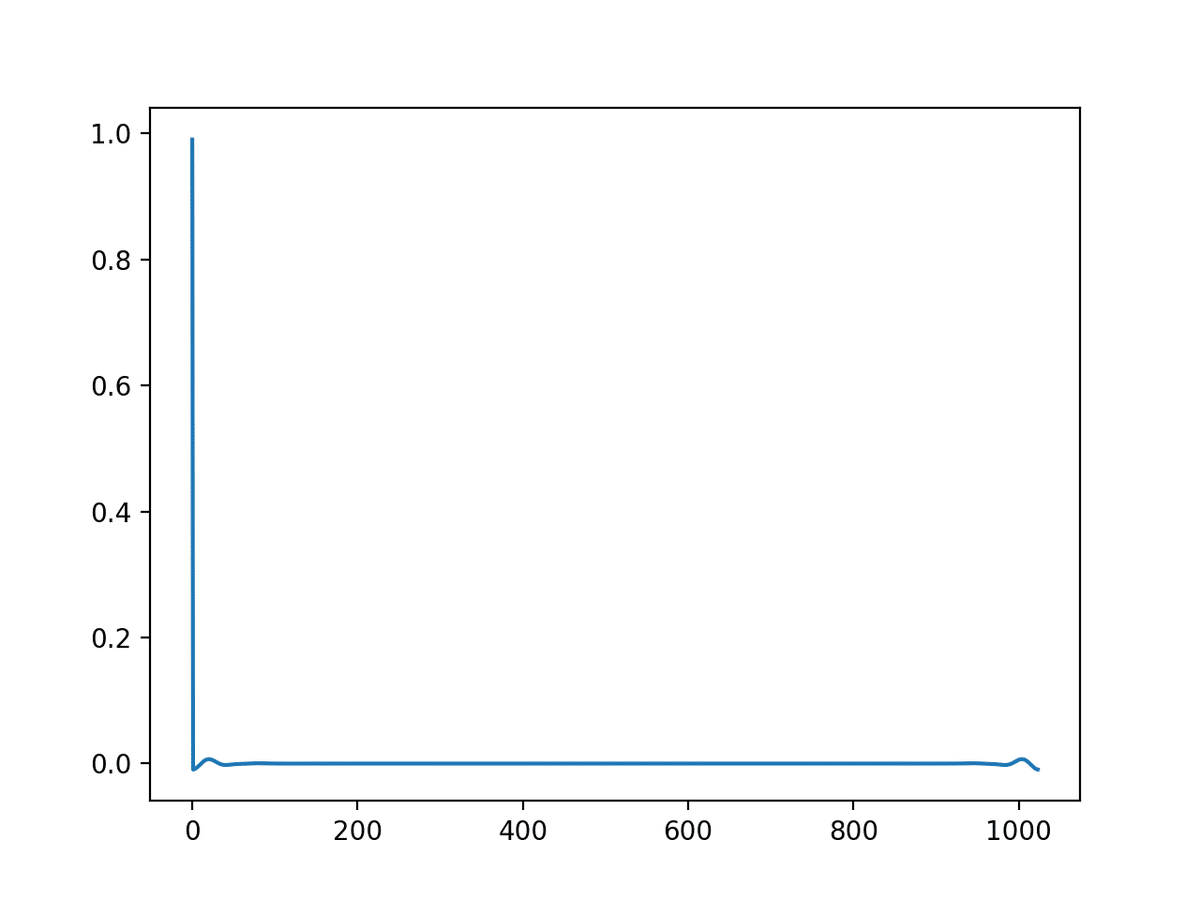
インパルス応答後半部分に振幅がある
すでにちゃんとしたインパルス応答っぽいですが,これでFIRフィルタ完成!とはいきません。よくよく見るとインパルス応答の後方に振幅が現れています。これは負の時間に振幅が発生している状態(因果性を満たしていない:非因果)のフィルタとなります。つまり実際には以下のようなフィルタになっているわけです。

実際に使用することは不可能
これは線形位相フィルタの大きな特徴です。線形位相フィルタは最大振幅を中心に左右対称形になっています。そして負の時間という概念は現実世界では起こり得ないので,このFIRフィルタはリアルタイムでの処理は不可能になります。ではこのフィルタの形を全く変えずに実際に使えるようにするにはどうすれば良いでしょうか。
時間シフトとその弊害
答えは簡単で,負の時間に振幅が現れないようにフィルタを時間シフトさせます。これは遅延を許すという書き方もできます。一般によく用いられる方法では,タップ長NでFIRフィルタを設計した場合,N/2だけ遅延を許す(フィルタを時間シフトする)ことで,フィルタが全て正の時間に収まり実際に使用できる因果的なフィルタになります。これは線形位相フィルタを使用する上で必ず発生する制約になります。

これなら実際に使用できるがフィルタを通すだけで遅延が発生する
注目すべきこと一つ目は最大振幅が大きく後ろにずれている点です。つまりこのフィルタを作用させると出力音はこのシフト分だけ遅延して出てくることになります。
よく"FIRフィルタは畳み込みで時間がかかるから遅延が発生する"という文脈が見受けられます。これは間違いではありませんが,最近は計算機やアルゴリズムの進歩により莫大なタップ数を多チャンネル並列に畳み込みを行っても実時間(一桁ms単位の遅延)で収まるようになってきています。それよりも数100ms単位で発生するような大きな遅延は,線形位相FIRフィルタの因果性を満たすために原理的に避けられない時間シフトによる遅延が原因であることがほとんどです。特に低周波数まで十分な解像度が欲しい場合には大きなタップ数をとることになりますが,それだけシフトさせる量も大きくなりフィルタ遅延として現れます。これが世間で言われている"低周波数を対象に線形位相フィルタを作ると遅延が大きくなる"ということです。
もう一つ注目すべきは線形位相FIRフィルタが左右対称形であるということです。線形位相FIRフィルタは最大振幅以前に最大振幅以後と対称な形が必ず発生します。これを音声信号に畳み込むと,出力された音の最初でわずかに音が漏れ出ているように聞こえます。これがいわゆるプリリンギングやプリエコーと呼ばれるものの正体です。線形位相フィルタではこれを避けることはできません。
最小位相フィルタ
線形位相FIRフィルタは位相シフトが発生しないという性質のために,音の面で遅延とプリリンギングの二つの犠牲が必要となります。一方処理を高速化させるなどリアルタイム性を重視する場合,線形位相特性よりも遅延とプリリンギングをなくす方を優先したいという要望も当然出てくるわけです。これは位相シフトを許すこと(波形が保存されない)によって実現が可能です。代表的な例として,位相シフトが最小な最小位相FIRフィルタがあります。
最小位相フィルタは必ず因果性を満たしており,位相シフトが最小となっています。そのため同じ振幅特性を持つフィルタの中では一番時刻0付近にエネルギーが集中しており,これは最も遅延が少ないとも言えます。
最小位相フィルタの設計や解析には,ラプラス変換,z変換,ヒルベルト変換といった学問をある程度知っている必要があります。そのためここでは詳細な設計方法までは言及しません。
発展的な内容:逆フィルタの作成
これまで記載した手法からある振幅特性を打ち消すフィルタやインパルス応答そのものを打ち消す逆フィルタを作ることも不可能ではありません。ただし後者の作成は原理的に難しい点も多く,特にディジタル信号処理や線形代数の知識が必要となります。
振幅特性だけ補正したい場合,Smaartなどで測定して得られた振幅特性のデータを反転させて,先の方法で線形位相FIRフィルタにすることはできますし,最小位相FIRフィルタでも作れます。ただしこの方法では,位相の補正は考慮されていません。後述する真の意味での逆フィルタと区別するためここでは逆振幅フィルタと表現します。
逆振幅フィルタはPAなどにおいて振幅特性を補正したいときには有用です。タップ数を多く取れば安定的に所望の振幅特性を実現できますし,線形位相特性を求めなければ最小位相フィルタとして遅延の少ないようにも作れます。これらは振幅特性の逆の特性と作っているということで主に音の聞こえ方について補正するものであり,物理的に系の特性を完全に打ち消すものではありません。
一方位相特性まで含めて真の意味での逆フィルタを作る場合(系の特性を完全に打ち消したいなど),打ち消したいインパルス応答をフーリエ変換して得られる複素数値の逆数をとる(1/複素数値)ことで逆フィルタとすることが多いです(他にも設計方法はいくつかあります)。ただしこれは色々な点で困難が生じるため上手くいくかは場合**によります。
安定な逆フィルタの作成は立体音響(研究成果としては境界音場制御やトランスオーラルシステム)や残響抑圧,雑音抑圧(MINTを利用した研究例が多くあります)など多くの音響研究で必要とされ,様々な研究がされてきました。こちらは音の聞こえはもちろん,音の物理的性質を制御するためにフィルタを作成します。そしてこれらの研究はFIRフィルタの進歩とともに発展してきたとも言えます。
**結論的には単純そのままでは上手くいかないインパルス応答を扱うことが多いということです。例えば測定したインパルス応答は有限インパルス応答ですが最小位相系であるとは限りません。その逆数をとって作成した逆フィルタは無限インパルス応答になり収束が保証されない,あるいは収束する場合でも非因果成分が発生するなどが起こり得ます。実用上は時間シフトの上で窓関数を用いて有限長で打ち切ることが多いかと思います。
またマイクロホン1対スピーカ1の場合はこの設計方法でも良いですが,一般に多対多(マイクロホン数M×スピーカ数N)の逆フィルタ作成は擬似逆行列という線形代数の問題になり、それなりに難しい話になります。現状,音質を満足しつつしっかりと逆特性になっているような多対多の逆フィルタ作成までは人の手無しでは難しいのですが,今後技術が進展すれば,イマーシブオーディオで多くのスピーカを複数のマイクで測定したデータをもとに特性を一括で自動補正したり,ラインアレイスピーカを複数地点で測定して一括で全キャビネットの自動補正するなどで実用化される未来があるかもしれません。
おまけ:窓関数を用いる方法と窓関数の話
これは無限区間のインパルス応答が手元にある場合(数式で定義できる場合や先の逆フィルタのような有限インパルス応答の逆数を取る場合),それを打ち切って有限長にしてしまうやり方です。無限の長さのインパルス応答を区切るということは,無限の長さのインパルス応答と有限幅の窓の積とも考えられます。
インパルス応答を打ち切る際に,ただ単にあるタップ長で打ち切る場合はいわゆる方形窓を用いていることと等価になります。方形窓はメインローブは鋭いですが,サイドローブがメインローブのすぐ近くにあります。そこで方形窓のようにある点でバッサリ打ち切るのではなく,窓の両端でテーパーをかけて滑らかに0へ収束させればサイドローブの高さは減らすことができます(これはメインローブの幅を広げるという犠牲によって得られるものです)。窓関数はこのように時間領域のデータを任意の長さで両端を0へ収束させながら打ち切るために用います。現在世の中では多くの窓関数が提案されていますが,数式内にcosineを取り入れているものが多いです(cosineのグラフの概形を見れば明らかですね)
窓を用いる方法では,求めている周波数応答を許容できる精度で近似するにはどの窓長,窓の形がふさわしいかをヒューリスティックに決める必要があります。窓の長さが短いほど打ち切ったインパルス応答も短くなるため,畳み込みの計算量は小さくなりますが,その分周波数応答の近似精度が下がります。逆に窓長を大きく取れば所望の周波数応答をより忠実に再現できることになりますが,その分畳み込みの際の計算量が大きくなります。
参考文献
[1]ディジタル信号処理, A.V.Oppenheim, R.W. Schafer著, 伊達玄 訳,コロナ社,1978
[2]信号とシステム, A.V.Oppenheim, A.S.Willsky著, 伊達玄 訳,コロナ社,1985
[3]ディジタル信号処理のエッセンス, 貴家仁志, オーム社, 2014
この記事が気に入ったらサポートをしてみませんか?
