
ベクトル演算を使ってゲームキャラクターを移動する方法
1. はじめに
高校時代に学んだベクトルが、2Dゲームのキャラクター移動に適用できることに驚いたため、調査・実装した結果をまとめる。ただし、下記を前提に読み進めてほしい。
(1) 2Dゲームで考える。
(2) キー入力の方法は、キーボードの上下左右キーのみに限定する。
(3) DxLib(C#版)を使用してコードを説明する。
2. キャラクターの移動
移動には、右・左・下・上の4つのキーを入力し、画面上のキャラクターを移動する(図1)。
例えば、上キーを押すと、キャラクターを上方向に移動する。
4つのキーを組み合わせると、斜め方向にも移動する。
例えば、右キーと下キーを入力すると、画面上のキャラクターを右斜めに下に移動する。
このキャラクターの移動方法は、色々方法がある。その中でも、今回は、ベクトルを使用した移動方法を取り上げる。
3. ベクトルを使用しない移動方法
まず、ベクトルを使用しない移動方法を考える。
3.1 仕様
下記に、ベクトルを使用しない移動方法を定義する。
(1) キー入力をチェックする
(2) 斜め移動のチェック
(2-1) 右キーまたは左キーを押下かつ下キーまたは上キーが押されていた場合
スピード = 0.707に設定する。
(2-2) それ以外は
スピード = 1.0に設定する。
(3) 右キーを押した場合
キャラクターX座標 = キャラクターX座標 + ピクセル数 * スピード
(4) 左キーを押した場合
キャラクターX座標 = キャラクターX座標 - ピクセル数 * スピード
(5) 下キーを押した場合
キャラクターY座標 = キャラクターY座標 + ピクセル数 * スピード
(6) 上キーを押した場合
キャラクターY座標 = キャラクターY座標 - ピクセル数 * スピード
式を要約する。最初にキー入力をチェックし、どのキーを押しているか確認する。次に、斜め移動のスピードを設定する。最後に、各キーに合わせてキャラクターの座標を加算・減算する。
ピクセル数は、プログラムを動作させて、任意の値を設定する。例えば、3とか6とかでよい。
3.2 斜め移動時のスピード設定法
斜め移動時のスピード=0.707は、ピタゴラスの定理から算出する。ピタゴラスの定理とは、直角三角形において2辺の長さが分かっていれば、残りの1辺の長さを計算できる。
例えば、辺の長さが1の直角三角形の斜辺(斜め)は、下記のように算出できる。
$$
{a^2 + b^2} = c^2
$$
$$
{1 + 1} = c^2
$$
$$
{c^2} = 2
$$
$$
c = \sqrt(2) = 1.41\ldots
$$
よって、斜め移動の距離は、約1.414倍の距離になるため、その効果的な速度を1に等しくするためには、下記の式となる。
$$
1 / \sqrt(2) = 0.707\ldots
$$
この値を設定することで、斜め移動がスムーズに行える。
3.3 実装例
下記にC#の実装例を示す。
namespace test{
class Program {
static void Main(string[] args) {
// ウィンドウモードで起動するように設定
DX.ChangeWindowMode(DX.TRUE);
// Dxlib の初期化
DX.DxLib_Init();
// 描画先を裏画面に設定
DX.SetDrawScreen(DX.DX_SCREEN_BACK);
//実行パスを取得する
string currentDirectory = Directory.GetCurrentDirectory();
//画像を取得する
int characterImage = DX.LoadGraph(currentDirectory + "\\..\\..\\img\\Image.png");
//キーの状態変数
byte[] keyState = new byte[256];
//X, Y座標
int x = 350;
int y = 50;
//スピード
float speed = 1.0f;
// メインループ
while (DX.ProcessMessage() == 0) {
// 画面をクリア
DX.ClearDrawScreen();
//キー入力をチェック
DX.GetHitKeyStateAll(keyState);
//斜め押しをしている場合は速度を変える
if (keyState[DX.KEY_INPUT_LEFT] == 1 || keyState[DX.KEY_INPUT_RIGHT] == 1) {
if (keyState[DX.KEY_INPUT_UP] == 1 || keyState[DX.KEY_INPUT_DOWN] == 1) {
speed = 0.707f;
} else {
speed = 1.0f;
}
} else {
speed = 1.0f;
}
// 各方向の移動計算
if (keyState[DX.KEY_INPUT_RIGHT] == 1) {
x += (int)(5 * speed);
}
if (keyState[DX.KEY_INPUT_LEFT] == 1) {
x -= (int)(5 * speed);
}
if (keyState[DX.KEY_INPUT_DOWN] == 1) {
y += (int)(5 * speed);
}
if (keyState[DX.KEY_INPUT_UP] == 1) {
y -= (int)(5 * speed);
}
DX.DrawGraph(x, y, characterImage, DX.TRUE);
// 裏画面の内容を表画面に反映
DX.ScreenFlip();
}
// Dxlib の終了処理
DX.DxLib_End();
}
}
}4. ベクトルを利用した上下左右移動
3.の実装方法も良いアイデアであるが、ベクトルを使用すると、より便利に実装できる。
4.1 ベクトルとは何か
ベクトルとは、「大きさと向きを持った量」のことである。
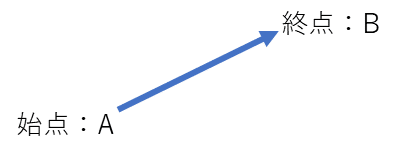
上記は、点Aから点Bへのベクトルを表したものである。このように、ベクトルは向きと大きさを持っている。
4.1.1 成分とは
成分とは、ベクトルの始点を原点に合わせた時に決まる終点の座標のことである。そのため、2Dのゲームでは、キャラクターの座標X、Yが成分として表せる。
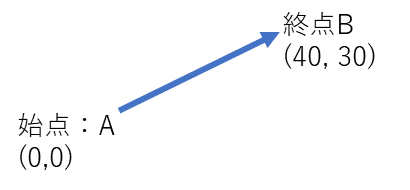
成分は、原点に合わせた時に決まる終点の座標であるため、(40, 30)が成分である。
4.1.2 ベクトルの大きさ(ノルム)とは
ベクトルの大きさとは、いわゆる「長さ」のことである。ノルムとも呼ばれる。
$$
ベクトルの大きさ =\sqrt{x^2 + y^2}
$$

上記の場合、ベクトルの大きさは次のように求める。
$$
ベクトルの大きさ =\sqrt{1600 + 900}
$$
$$
ベクトルの大きさ ={50}
$$
4.1.3 方向とは
方向とは、原点からみた示す向きのことである。
4.2 ベクトルの加算
2つのベクトルを加算することができる。
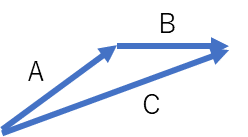
上記は、ベクトルの加算のイメージ図である。A点とB店を加算し、新たなベクトルCができていることが分かる。
4.3 ベクトルの正規化
ベクトルの正規化とは、ベクトルの方向は保持しつつ、その長さ(大きさ)を1とするものである。
$$
ベクトルの長さ(大きさ) =\sqrt{x^2 + y^2}
$$
$$
正規化されたベクトル\hat{\mathbf{v}} = \frac{1}{|\mathbf{v}|} \begin{pmatrix} x \ y \end{pmatrix} = \begin{pmatrix} \frac{x}{\sqrt{x^2 + y^2}} \ \frac{y}{\sqrt{x^2 + y^2}} \end{pmatrix}
$$
4.4 ベクトルの乗算
ベクトルの乗算とは、各成分を同じ数で乗算する。これによって、ベクトルの向きは変えずに大きさを変えることができる。
$$
k \mathbf{v} = k \begin{pmatrix} x \ y \end{pmatrix} = \begin{pmatrix} kx \ ky \end{pmatrix}
$$
4.5 ベクトルの実装例
プログラムでベクトルの加算、乗算、正規化をするプログラムを示す。
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using SystTm.Threading.Tasks;
namespace Test {
//ベクトルクラス
public class Vector {
public double X { get; set; }
public double Y { get; set; }
//コンストラクタ
public Vector(double x, double y) {
X = x;
Y = y;
}
//加算
public void Add(Vector _vec) {
X += _vec.X;
Y += _vec.Y;
}
//乗算
public void Scale(double scale) {
X *= scale;
Y *= scale;
}
//正規化
public void Normalize() {
double length = Math.Sqrt(X * X + Y * Y);
if (length > 0) {
X /= length;
Y /= length;
}
}
}
}
上記は、ベクトルクラスを表すVectorクラスである。処理としては下記を実行している。
(1) コンストラクタでx, yを設定する
(2) Addで、入力があったベクトルを加算する
(3) Scaleで入力があったベクトルを乗算している。
(4) Normalizeで、長さを求めx、yを割っている。
5. ベクトルを用いたキャラクター移動
ベクトルを用いたキャラクター移動に関して示す。
5.1 ベクトルを使用するメリット
ベクトルを使用すると、斜め移動時の条件分岐を考える必要がなくなる。3項では、下記のようにして斜め入力時の速度を決定していた。
//斜め押しをしている場合は速度を変える
if (keyState[DX.KEY_INPUT_LEFT] == 1 || keyState[DX.KEY_INPUT_RIGHT] == 1) {
if (keyState[DX.KEY_INPUT_UP] == 1 || keyState[DX.KEY_INPUT_DOWN] == 1) {
speed = 0.707f;
} else {
speed = 1.0f;
}
} else {
speed = 1.0f;
}
// 各方向の移動計算
if (keyState[DX.KEY_INPUT_RIGHT] == 1) {
x += (int)(5 * speed);
}
if (keyState[DX.KEY_INPUT_LEFT] == 1) {
x -= (int)(5 * speed);
}
if (keyState[DX.KEY_INPUT_DOWN] == 1) {
y += (int)(5 * speed);
}
if (keyState[DX.KEY_INPUT_UP] == 1) {
y -= (int)(5 * speed);
}上記の処理は、ベクトルを使用すると、下記のベクトルに置き換えることで代替え可能である。
・右方向を表すベクトル(1, 0)
・左方向を表すベクトル(-1, 0)
・上方向を表すベクトル(0, -1)
・下方向を表すベクトル(0, 1)
・右上方向を表すベクトル(1, -1)
・右下方向を表すベクトル(1, 1)
・左上方向を表すベクトル(-1, -1)
・左下方向を表すベクトル(-1, 1)
最後に、ここにスピードをかけてあげれば、斜めの考慮する必要がなくなる。
5.2 ベクトルを用いたキャラクター移動の仕様
ベクトルを考慮すると下記の式となる。
(0) 入力状態をチェックする。
(1)方向ベクトルを作成する
下記のイメージに示すような大きさ1の方向ベクトルを作成する。
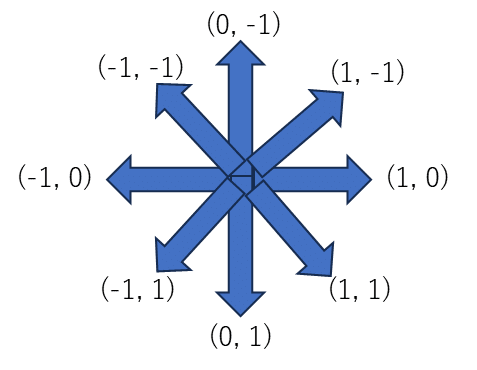
(1-1) 右キーを押した場合
(1, 0)の方向ベクトルを作成する。
(1-2) 左キーを押した場合
(-1, 0)の方向ベクトルを作成する。
(1-3) 下キーを押した場合
(0, 1)の方向ベクトルを作成する。
(1-4) 上キーを押した場合
(0, -1)の方向ベクトルを作成する。
(2) キー押下チェック
(2-1) キーが押されている場合
$$
{大きさ = sqrt(座標X + 座標Y) }
$$
斜めの場合は
$$
{sqrt(1 + 1) = 1.414}
$$
となり、1を超える場合があるため、方向ベクトルを正規化する。
$$
{正規化した方向ベクトルX = 座標X / 大きさ}
$$
$$
{正規化した方向ベクトルY = 座標Y / 大きさ}
$$
$$
{速度ベクトルX = 正規化したベクトルX * スピード}
$$
$$
{速度ベクトルY = 正規化したベクトルY * スピード}
$$
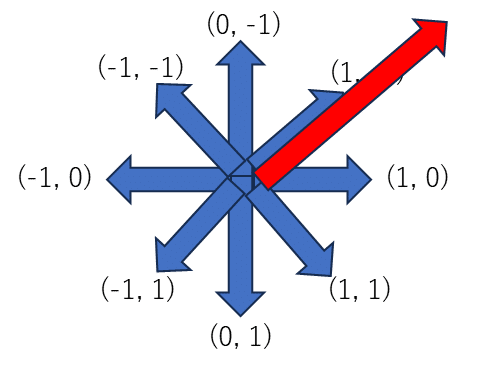
(2-2) それ以外
(0,0)の方向ベクトルを作成する。
(3) 座標を移動する

$$
{プレイヤーのX座標 = プレイヤーのX座標 + 速度ベクトルX}
$$
$$
{プレイヤーのY座標 = プレイヤーのY座標 + 速度ベクトルY}
$$
5.3 実装例
実装例を下記に示す。
namespace Akaishi {
class Program {
static void Main(string[] args) {
// ウィンドウモードで起動するように設定
DX.ChangeWindowMode(DX.TRUE);
// Dxlib の初期化
DX.DxLib_Init();
// 描画先を裏画面に設定
DX.SetDrawScreen(DX.DX_SCREEN_BACK);
//実行パスを取得する
string currentDirectory = Directory.GetCurrentDirectory();
//画像を取得する
int characterImage = DX.LoadGraph(currentDirectory + "\\..\\..\\img\\Image.png");
//キーの状態変数
byte[] keyState = new byte[256];
//X, Y座標
Vector position = new Vector(350, 50);
Vector velocity = new Vector(0, 0);
//スピード
float speed = 5;
// メインループ
while (DX.ProcessMessage() == 0) {
// 画面をクリア
DX.ClearDrawScreen();
//キー入力をチェック
DX.GetHitKeyStateAll(keyState);
bool isMoving = false;
//方向を表すベクトルを作成
Vector direction = new Vector(0, 0);
// キー入力に応じた方向ベクトルの計算
//右キー押下の場合
if (keyState[DX.KEY_INPUT_RIGHT] == 1) {
direction.Add(new Vector(1, 0));
isMoving = true;
}
//左キー押下の場合
if (keyState[DX.KEY_INPUT_LEFT] == 1) {
direction.Add(new Vector(-1, 0));
isMoving = true;
}
//下キー押下の場合
if (keyState[DX.KEY_INPUT_DOWN] == 1) {
direction.Add(new Vector(0, 1));
isMoving = true;
}
//上キー押下の場合
if (keyState[DX.KEY_INPUT_UP] == 1) {
direction.Add(new Vector(0, -1));
isMoving = true;
}
//キーが押されている場合は
if (isMoving) {
//正規化する
direction.Normalize();
//スピード分進む
direction.Scale(speed);
//代入
velocity = direction;
}
else {
//キー入力がないので停止する
velocity = new Vector(0, 0);
}
//速度を加算する
position.Add(velocity);
DX.DrawGraph((int)position.X, (int)position.Y, characterImage, DX.TRUE);
// 裏画面の内容を表画面に反映
DX.ScreenFlip();
}
// Dxlib の終了処理
DX.DxLib_End();
}
}
}
6. 終わりに
今回は、ベクトル演算を用いて2Dゲームのキャラクター移動の実装方法を説明した。ベクトル演算自体は高校生で学習するが、ゲームキャラクターの移動に適用すると非常に効果的であるとわかった。
なお、ゲームパッドのアナログスティックを用いると、もう少し考える必要がありそうである。
