
自然数を4行に並べる
自然数(1,2,3,・・・)は一直線状に並んでいるイメージが強い。しかし、螺旋状に並べたり、2行、3行、4行、・・・に並べることもできる。


上図のように自然数を4行に並べた場合、第一行は「4で割る」と「1余る数」が並ぶ。同様に、第二行は「2余る数」であり、第三行は「3余る数」で、第四行は「余りが0」の4の倍数が並ぶ。
余りで分類すると「剰余類」となり集合の記号で示すと{0,1,2,3}となる。
さて、上図を見ると、「2」以外の素数は第一行と第三行に存在している。特に第三行には素数が多く並んでいるように見える。(○印は素数である。)
上図のような素朴な数表で整数論を研究し論じたのは古代ギリシャ時代に
始まる。エウクレイデス(ユークリッド)は既知の素数から新しい素数のいくつかを生成する式「2^n−1」を用いて、「2^n−1」が素数であれば「2^(n-1)×(2^n−1)」は完全数になることを証明している。
(「n=2」とすると「2^(n-1)×(2^n−1)」は「6」となる。)
完全数とは「6」のように、その全ての約数の和(1+2+3)が元の数「6」になるものである。
その後、メルセンヌ(1588~1648)は「2^n−1」が素数になるのは、nが次の十一個の素数のときである、と主張する。
(n=2,3,5,7,13,17,19,31,67,127,257)
それで、今日では「2^n−1」型の数は「メルセンヌ数」と呼ばれ、素数である場合は「メルセンヌ素数」と呼ばれている。
今日では、メルセンヌの予想で「67」と「257」は誤りであることが分かっている。そして、新たに「61」「89」「107」「521」 「607」・・・「57885161」などが素数を生成することが示され、2018年には51番目のメルセンヌ素数が発見されている。
「2の累乗」を用いて素数を絞り込む方法はフェルマー(1607~1665)によって極まる。

上の式でnの値が「0, 3, 5, 17, 257」の時は素数になるとフェルマーは予想する。
しかし、「n=257」によって生成される数は合成数になることが示される。
(4294967297=641×6700417)
このことを示したのは、スイス(バーゼル)生まれのオイラー(1707~1783)である。
日本は江戸時代中期であり、徳川吉宗が八代将軍として在位(1716~1745)していた頃で、和算家が活躍していた。江戸の人口は百万人を超え、関孝和は1708年に没しているが、和算は最盛期をむかえていた。
オイラーは、自然数から素数になりそうな数を絞るのではなく、素数そのものを生成する多項式を作成する。
その時に参考にしたのが、前出の自然数を四行に並べた数表ではないのかと筆者は推測する。一行目の素数は「4で割って1余り」、三行目の素数は「4で割って3余る」のである。
そこから、オイラーは「(4n+1)(4n+3)」と、それぞれ「4を引いた式」である「(4n−3)(4n−1)」を見出して、試行錯誤を繰り返したのではないのか。 → (4n−3)(4n−1)=16n^2−16n+3 → 16(n^2−n+3/16)
そして、次の式にたどり着いたと想われる。
F(n)=n^2−n+p (pは次のいずれかの素数:2,3,5,11,17,41)
(このpの値は「オイラーの幸運数」と呼ばれていて深い意味をもつ。)
F(n)=n^2−n+41 この式では、nの値が「1,2,3,・・・,39,40」の「すべてについて素数を生成する」のである。オイラーはこの式について、1771年、ベルヌーイに手紙で知らせている。
(なお、1797年にルジャンドルは「n^2+n+41」と同値であることを示して、こちらの表現を用いているという。)
このオイラーの素数生成多項式は、無数にある素数のすべてを生成するわけではない。しかし、「n=40」を超えて生成される数は高い確率で素数になることが分かっており、無数の素数を生成するのではないかと予想されている。
さて、素数を生成する「2の累乗の式」では勇み足を踏んでいたフェルマーであるが、「4n+1」型の素数(5, 13, 17, 41,・・・)は二個の平方数の和に表すことができることを証明している。
そして、「4n+1」型素数は「ピタゴラス素数」と呼ばれるようになる。
その理由は次の例によって想像できるかも知れない。
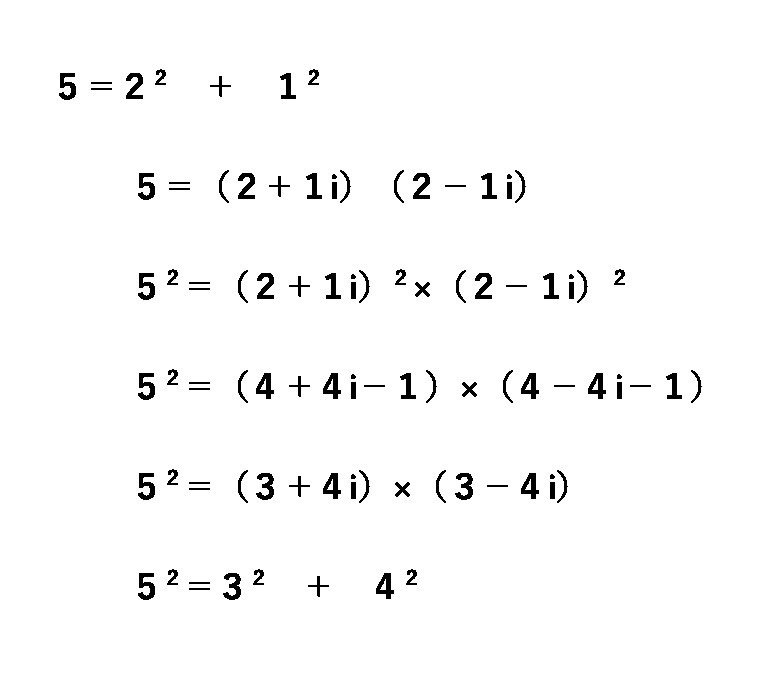
ピタゴラスの定理を満たす整数の組は無数に存在する。
(3,4,5)や(5,12,13)は有名である。
この整数組の斜辺にあたる最大数は素数であり、「4n+1」型であることをフェルマーは証明したのである。
