
kaggleコンペ初挑戦!タイタニック号の生存予測で学んだ機械学習の基礎②
皆さん、こんにちは!今回は「タイタニック号の生存予測」を通して学んだ機械学習の基礎解説の第2回目です。
初めてKaggleコンペに挑戦し、データ分析の流れやモデル構築のコツを少しずつ理解できるようになってきました。
もしまだ前回の「kaggleコンペ初挑戦!タイタニック号の生存予測で学んだ機械学習の基礎①」を読んでいない方は、こちらもぜひご覧ください。
前回では、データの準備や基本的な前処理について解説していますので、今回の内容がよりスムーズに理解できると思います。
それでは、今回はさらに一歩進んで、特徴量エンジニアリングを行い、予測精度を上げるためのステップに入っていきます!
特徴量エンジニアリングとは?
まず、「特徴量」とは、モデルにとって意味のあるデータの属性(列)を特徴量と定義します。
※ただし、モデルの性能に良い影響を与えるものに限る
そして「特徴量エンジニアリング」とは、前述した「特徴量」の「エンジニアリング」(工学)ということなので、つまり、モデルの性能に良い影響を与える説明変数を作り出すこと

実行環境
Windows11
Python3
Kaggle
分析の流れ
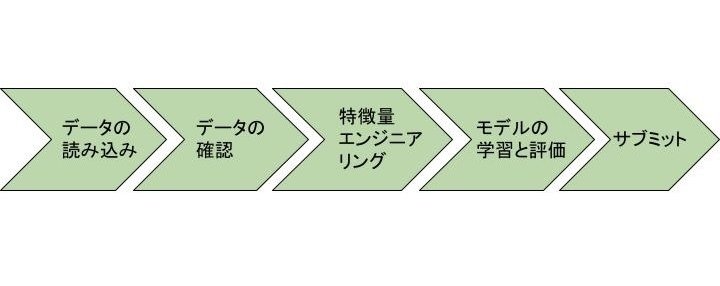
実装
まずは、最終的な完成コードです。
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
# ファイルの読み込み
train_df = pd.read_csv('/kaggle/input/titanic/train.csv')
test_df = pd.read_csv('/kaggle/input/titanic/test.csv')
sample_sub = pd.read_csv('/kaggle/input/titanic/gender_submission.csv')
# 訓練データとテストデータを結合しall_dfを作成
all_df = pd.concat([train_df,test_df],axis=0).reset_index(drop=True)
# 訓練データとテストデータを判定するためのカラムを作成
all_df['Test_Flag'] = 0
all_df.loc[train_df.shape[0]: , 'Test_Flag'] = 1
# 「機械学習の基礎1」で作成した特徴量
all_df['Age'] = all_df['Age'].fillna( all_df['Age'].median())
all_df['Fare'] = all_df['Fare'].fillna( all_df['Fare'].median())
all_df['Embarked'] = all_df['Embarked'].fillna('NaN')
all_df['FareBand'] = pd.qcut(all_df['Fare'], 4)
all_df['AgeBand'] = pd.qcut(all_df['Age'], 4)
# 今回新たに作成した「同乗した家族の人数」に関する特徴量
all_df['FamilySize'] = all_df['SibSp'] + all_df['Parch'] + 1
all_df['MedF'] = all_df['FamilySize'].map(lambda s: 1 if 2 <= s <= 4 else 0)
all_df['LargeF'] = all_df['FamilySize'].map(lambda s: 1 if s >= 5 else 0)
all_df['Alone'] = all_df['FamilySize'].map(lambda s: 1 if s == 1 else 0)
# One-Hot_Encodingで変換
all_df = pd.get_dummies(all_df, columns= [
'Sex', 'Pclass','AgeBand','FareBand','Embarked'
], dtype='float')
# 前処理を施したall_dfを訓練データとテストデータに分割
train = all_df[all_df['Test_Flag']==0]
test = all_df[all_df['Test_Flag']==1].reset_index(drop=True)
target = train['Survived']
# 今回学習に用いないカラムを削除
drop_col = [
'PassengerId','Age',
'Ticket',
'Fare','Cabin',
'Test_Flag','Name','Survived'
]
train = train.drop(drop_col, axis=1)
test = test.drop(drop_col, axis=1)
# 訓練データの一部を検証データに分割
X_train ,X_val ,y_train ,y_val = train_test_split(
train, target,
test_size=0.2, shuffle=True,random_state=0
)
# モデルを定義し学習
model = LogisticRegression()
model.fit(X_train, y_train)
# 訓練データに対しての予測を行い、正答率を算出
y_pred = model.predict(X_train)
print(accuracy_score(y_train, y_pred))
# 検証用データでモデルを評価
y_pred_val = model.predict(X_val)
print(accuracy_score(y_val, y_pred_val))
# テストデータを予測
test_pred = model.predict(test)
# 予測結果をサブミットするファイル形式に変更
sample_sub["Survived"] = np.where(test_pred>=0.5, 1, 0)
display(sample_sub.head(10))
# 提出ファイルを出力
sample_sub.to_csv("submission.csv", index=False)各columnの意味は以下の通りです。
PassengerId : 乗客識別ユニークID
Survived : 1が生存、0が死亡 ← テストデータにおけるSurvivedを予測するのが本課題
Pclass : チケットのクラス、1st(上層)=1, 2nd(中級)=2, 3rd(下層)=3
Name : 乗客の名前
Sex : 男性(male), 女性(female)
Age : 年齢
SibSp : 同乗している兄弟、配偶者の人数
Parch : 同乗している両親、子供の数
Ticket : チケットの番号
Fare : 乗船料金
Cabin : 部屋番号
Embarked : 乗船した港(S=Southampton, C=Cherbourg, Q=Queenstown)
今回は、予測モデルの性能を向上させるために、新たな特徴量を作成し、予測モデルの改善に取り組んでみました。
前回の記事で解説した分析結果から、同伴している兄弟姉妹( SibSp )や親子( Parch )の人数と生存率には関係性があることがわかりました。
今回は、この知見を切り口に探索的データ分析(EDA)を行っていきたいと思います。
探索的データ分析(EDA)は、後ほど解説します。
それでは、流れに沿って詳しく解説していきます。
1.データの読み込み
import numpy as np
import pandas as pd
# 訓練データ読み込み
train_df = pd.read_csv("/kaggle/input/titanic/train.csv")
# テストデータ読み込み
test_df = pd.read_csv("/kaggle/input/titanic/test.csv")
# 提出データ読み込み
sample_sub = pd.read_csv("/kaggle/input/titanic/gender_submission.csv")2.データの確認
各特徴量と生存率の関係を再度確認していきます。
まず、SibSpの特徴量と生存率の関係を確認。
import matplotlib.pyplot as plt
import seaborn as sns
# SibSpについて可視化
sns.countplot(x="SibSp", hue="Survived", data=train_df)
plt.show()
>>>出力結果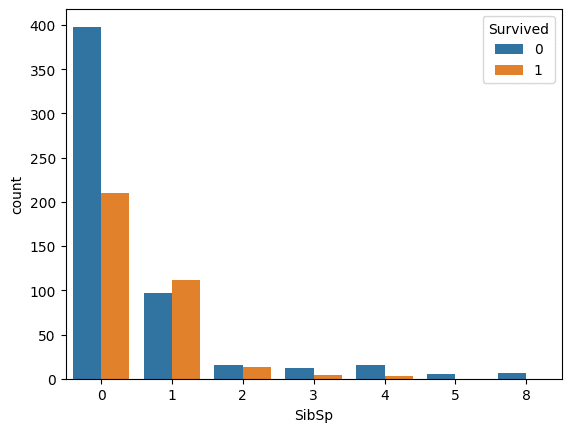
グラフを見ると、同乗した兄弟、姉妹、配偶者の人数が1~2人の人の生存率が高いことがわかります。
次に、Parchの特徴量と生存率の関係を確認。
# Parchについて可視化
sns.countplot(x="Parch", hue="Survived", data=train_df)
plt.show()
>>>出力結果
グラフを見ると、同乗した親と子供の人数が1~3人の人の生存率が高いことがわかります。
3.探索的データ分析(EDA)とは?
EDA (Exploratory Data Analysis) とは、データを理解し、分析の方向性を決めるための最初のステップです。
EDAの目的は、データの基本的な特徴や傾向、パターン、潜在的な問題(例:欠損値や異常値)を把握することです。
機械学習におけるデータ準備段階の一環として行われ、以降のモデル構築に役立つ重要な情報を見つけ出します。
EDAは、データの基本的な理解と分析の準備のために不可欠なプロセスです。分析やモデル構築の土台となる部分なので、丁寧に行うことでより効果的なモデルを作るための手助けとなります。
EDAでは、次のような作業を行います。
記述的分析
解決すべき課題の理解
変数の特徴を掴む
前処理
可視化
データセットの準備
4.新たな特徴量の作成と可視化
データを確認した際に、以下のような関係があることが読み取れました。
SibSpのグラフから、同乗した兄弟、姉妹、配偶者の人数が1~2人の人の生存率が高い
Parchのグラフから、同乗した親と子供の人数が1~3人の人の生存率が高い
これらをもとに再考すると、「同乗した家族の人数と生存率には重要な関係があるのではないか」という仮説を立てることができます。
それでは実際に、データを集計/可視化し仮説を検証していきましょう。
まずは、下記のようなコードを記述し、「同乗した家族の人数」という新たな特徴量を作成します。
# 新たな特徴量を作成
# 同乗した家族の人数 = 兄弟・配偶者の人数 + 両親・子供の人数 + 本人
train_df["FamilySize"] = train_df["SibSp"] + train_df["Parch"] + 1可視化します。
# 新たに作成したFamilySizeと生存率の関係を可視化
sns.countplot(x="FamilySize", hue="Survived", data=train_df)
plt.show()
>>> 出力結果
グラフを見ると、以下のようなことが確認できます。
全体に占める1人で乗船した人の割合は大きいが、その生存率は低い
2~4人の家族で乗船した場合、生存率は高くなっている
5人以上の家族で乗船した場合、生存率は低くなっている
5.新たな特徴量について集計
次は集計を行い、割合を計算して確認してみます。
訓練データにおける家族人数毎の割合と生存率を算出します。
# 家族人数毎のデータに含まれる割合
display(train_df["FamilySize"].value_counts(ascending=False, normalize=True)) # ascending=False:降順、normalize=True:出現回数ではなく、その割合(全体に対する%)を返す
>>> 出力結果
proportion
FamilySize
1 0.602694
2 0.180696
3 0.114478
4 0.032548
6 0.024691
5 0.016835
7 0.013468
11 0.007856
8 0.006734
dtype: float64訓練データにおける家族人数毎の割合は、1人で乗船した人が全体の約6割、2~4人の家族で乗船した割合が全体の約3割ということがわかりました。
以下で使用している「crosstab : クロス集計表(クロスタブ)」は、行と列にカテゴリカルデータを配置し、それぞれの組み合わせの頻度をカウントします。
# 家族人数毎の生存率
# normalize="index":正規化(各行の合計が1(または100%)になるように値がスケーリング)
display(pd.crosstab(train_df["FamilySize"], train_df["Survived"], normalize="index"))
>>> 出力結果
Survived 0 1
FamilySize
1 0.696462 0.303538
2 0.447205 0.552795
3 0.421569 0.578431
4 0.275862 0.724138
5 0.800000 0.200000
6 0.863636 0.136364
7 0.666667 0.333333
8 1.000000 0.000000
11 1.000000 0.000000(0 : 死亡、1 : 生存)
訓練データにおける家族人数毎の生存率は、1人で乗船した人が生存率が3割、2~4人の家族で乗船した人の生存率は約5割を超えています。
集計から以下のことが確認できました。
1人で乗船した人が全体の約6割で、生存率が3割程度
2~4人の家族で乗船した割合が全体の約3割で、生存率は5割を超えている
5人以上の家族で乗船した割合が全体の約1割で、生存率は1~3割程度
6.データセットの準備
今回は、以下のような方針で新たな特徴量を作成しデータセットに追加します。
SibSpとParchから新たに「同乗した家族の人数」の特徴量を作成
同乗した家族の人数から、1人、2~4人、5人以上の3つのカテゴリを作成
# 同乗した家族の人数を追加
all_df["FamilySize"] = all_df["SibSp"] + all_df["Parch"] + 1# 同乗した家族の人数をもとに分割
# 2~4人で乗船した人を表す特徴量を追加
all_df["MedF"] = all_df["FamilySize"].map(lambda s: 1 if 2 <= s <= 4 else 0)
# 5人以上で乗船した人を表す特徴量を追加
all_df["LargeF"] = all_df["FamilySize"].map(lambda s: 1 if s >= 5 else 0)
# 1人で乗船した人を表す特徴量を追加
all_df["Alone"] = all_df["FamilySize"].map(lambda s: 1 if s == 1 else 0)ここで、これらの新たな特徴量をデータセットに追加したコードをまとめてみます。
import numpy as np
import pandas as pd
# 各ファイルの読み込み
train_df = pd.read_csv('/kaggle/input/titanic/train.csv')
test_df = pd.read_csv('/kaggle/input/titanic/test.csv')
sample_sub = pd.read_csv('/kaggle/input/titanic/gender_submission.csv')
# データ全体にまとめて処理を行うために、訓練データとテストデータを結合
all_df = pd.concat([train_df, test_df], axis=0).reset_index(drop=True)
all_df["Test_Flag"] = 0
all_df.loc[train_df.shape[0]: , "Test_Flag"] = 1
# 前回の記事で作成した特徴量
all_df["Age"] = all_df["Age"].fillna(all_df["Age"].median())
all_df["Fare"] = all_df["Fare"].fillna(all_df["Fare"].median())
all_df["Embarked"] = all_df["Embarked"].fillna("NaN")
all_df["FareBand"] = pd.qcut(all_df["Fare"], 4)
all_df["AgeBand"] = pd.qcut(all_df["Age"], 4)
# 今回新たに作成した特徴量 -----------------------------------------------------
all_df["FamilySize"] = all_df["SibSp"] + all_df["Parch"] + 1
all_df["MedF"] = all_df["FamilySize"].map(lambda s: 1 if 2 <= s <= 4 else 0)
all_df["LargeF"] = all_df["FamilySize"].map(lambda s: 1 if s >= 5 else 0)
all_df["Alone"] = all_df["FamilySize"].map(lambda s: 1 if s == 1 else 0)
# ----------------------------------------------------------------------------
# カテゴリカル変数をOne-Hot Encodeingで数値化
all_df = pd.get_dummies(all_df, columns= [
'Sex', 'Pclass','AgeBand','FareBand','Embarked'
], dtype='float')7.訓練データとテストデータの作成
作成したデータセットを用いて訓練データと検証データを作成していきます。
from sklearn.model_selection import train_test_split
# 前処理を施したall_dfを訓練データとテストデータに分割
train = all_df[all_df["Test_Flag"] == 0]
test = all_df[all_df["Test_Flag"] == 1].reset_index(drop=True)
target = train["Survived"]
# 今回学習に用いないカラムを削除
drop_col = [
"PassengerId", "Age",
"Ticket", "Fare", "Cabin",
"Test_Flag", "Name", "Survived"
]
train = train.drop(drop_col, axis=1)
test = test.drop(drop_col, axis=1)
# 訓練データの一部を分割し検証データを作成
X_train, X_val, y_train, y_val = train_test_split(train, target,
test_size=0.2, shuffle=True, random_state=0)8.モデルの学習と評価
今回も、ロジスティック回帰を用います。
ロジスティック回帰は、前回の記事で解説しているので、わからない方はこちらをご覧ください。
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
# モデルを定義し学習
model = LogisticRegression()
model.fit(X_train, y_train)
# 訓練データに対しての予測を行い、正答率を算出
y_pred = model.predict(X_train)
print(accuracy_score(y_train, y_pred))
>>> 出力結果
0.80898876404494389.ファイル作成とサブミット
作成した予測モデルを用いて、テストデータを予測し、結果をサブミット(提出)します。
# テストデータを予測
test_pred = model.predict(test)
# 予測結果をサブミットするファイル形式に変更
# np.where(...): NumPyの関数で、条件に基づいて値を置き換える
sample_sub["Survived"] = np.where(test_pred >= 0.5, 1, 0) # 生存確率が0.5以上の乗客を生存(1)、それ未満の乗客を非生存(0)としてフラグ付け
# 確認
display(sample_sub.head())
>>> 出力結果
PassengerId Survived
0 892 0
1 893 0
2 894 0
3 895 0
4 896 1# 提出ファイルを出力
sample_sub.to_csv("submission.csv", index=False)まとめ
以上が、Kaggleのタイタニック号生存予測コンペで学んだ機械学習の基礎の2回目でした。
スコアは、前回より少し上昇し0.77621でした。この結果は、初心者としては一つの目標を達成できたと感じています。
データの分析や特徴量の作成がスコアに与える影響を実感できたことは、今後の分析にも役立つ貴重な学びでした。
また、単に機械学習の技術だけでなく、データの裏にある「人間的な視点」や「問題の本質」を意識することの重要性も再確認しました。
今後も試行錯誤しながら、さらに精度の高い予測モデルを目指していきたいと思っています。
最後までお読みいただき、ありがとうございました!
