2.三極管を用いた増幅回路の設計

本節では、三極管の仕組みで説明した内容を用いて、増幅回路を設計してみます。

三極管の仕組みではプレート電圧を固定してグリッドバイアスを変化させると、プレートからカソードに向かって流れる電流が変化しました。この電流を出力電圧に変換するには、プレート側の電源端子とプレートの間にR(Ω)の抵抗を挟み(これを負荷抵抗と呼びます)、プレートと負荷抵抗の間から電圧を取り出します。プレートからカソードに流れる電流(プレート電流) がIp(A)であるとき、この抵抗による電圧降下はR×Ip (V)となります。よって、出力される電圧は、下の図のように電源電圧が200Vの場合、200-R×Ip(V)となります。

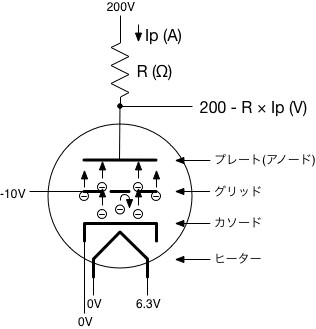
図．プレート電流から出力電圧への変換

これでは入力信号が負のバイアスを中心とした増減となり、出力信号が正の電圧を中心とした増減となります。

これを両者ともに0Vを中心とした増減になるようにし、カソードバイアス回路として回路を作成すると、以下の図のようになります。グリッドの電圧は、信号入力が無い場合を考えます。このとき、グリッド電圧はグラウンドに対して0Vとなります。プレート電圧は230Vです。カソード電圧は、プレート電流Ip〔A〕にカソード抵抗1kΩを掛けた1×Ip〔V〕だけグラウンドより高くなりますので、実際のプレート電圧は230-Ip〔V〕になります。

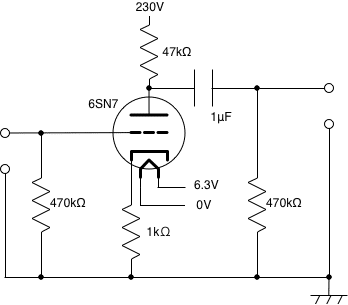
図．周辺回路を追加した増幅回路

真空管の三定数

三極真空管には次のような三つの定数があり、これを三定数と呼びます。
1.増幅率(μ)
2.相互コンダクタンス(gm)：単位はジーメンス〔S〕
3.内部抵抗(rp)またはプレート抵抗：単位はオーム〔Ω〕
これらのうち後者二つの定数は、上に示した二つの特性の傾き(曲線なので厳密には接線の傾き)によって表されます。

増幅率の定義は、ある一定のプレート電流を保つためにプレート電圧の微小変化量に対するグリッド電圧の微小変化量の比、すなわちグリッド電圧の微小電荷量をプレート電圧の微小変化量で割ったものです。電圧を電圧で割ったものなので、単位は無次元(単位なし)となります。

相互コンダクタンスの定義は、一定のプレート電圧において、グリッド電圧の微小変化によってプレート電流が微小変化します。このグリッド電圧の微小変化量に対するプレート電流の微小変化量の比、すなわちプレート電流の微小変化量をグリッド電圧の微小変化量で割ったものを相互コンダクタンスと呼びます。この値は電流を電圧で割ったもの〔A/V〕であり、電圧を電流で割った抵抗の単位であるオーム〔Ω、ohm〕=〔V/A〕の逆数であったことから、昔は単位としてモー〔Ωを上下逆に書いたもの、もしくはmho〕が用いられていましたが、現在はジーメンス〔S〕が用いられています。

内部抵抗の定義は、一定のグリッド電圧において、プレート電圧の微小変化によって、プレート電流が微小変化します。この度合いは真空管内に一種の抵抗があり、その大小によるものであると考えられますので、プレート電圧の微小変化量とプレート電流の微小変化量の比を内部抵抗もしくはプレート抵抗と呼びます。単位はオーム〔Ω〕です。

例えば、Eg=-5V、Ep=200Vにおける相互コンダクタンスgmは以下のEg-Ip図の接線の傾きになります。この接線は、Egが5Vだけ増えたときIpが12mAだけ増えているので、gm=12mA/5V=2.4mSとなります。

図．Eg=-5V，Ep=200Vにおける12AU7の相互コンダクタンスgm

一方、Eg=-5V、Ep=200Vにおける内部抵抗rpの値は、以下のEp-Ip図の接線の傾きの逆数となります。この接線はEpが80Vだけ増えたときIpが12mAだけ増えているので、傾きの逆数はrp=80V/12mA=6667Ωとなります。

図．Eg=-5V，Ep=200Vにおける12AU7の内部抵抗rp

これら三つの定数の間にはμ=gm×rpの関係があります。例えば、上の例ではgm=0.0024S，rp=6667Ωよりμ=0.0024×6667=16となります。

特性曲線に基づく増幅回路の設計

前に示した12AU7の特性曲線から、実際に抵抗負荷の場合の増幅回路を設計してみましょう。ここではまず、Eg=-5V、Ep=200Vを中心として計算してみます。次の図のように、Eg=-5V，Ep=200V、Ip=12mAの点において、Ep-Ip曲線の接線に対してだいたい直交するように直線を引いてみます。これを負荷直線(ロードライン)と呼びます。

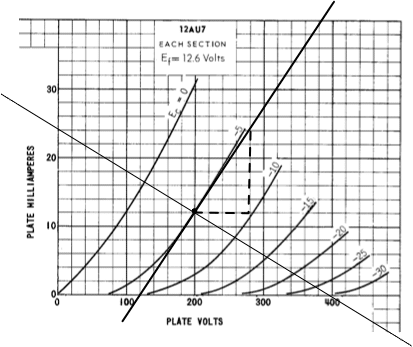
図．Ep=200V，Ip=12mA，Eg=-5Vにおける負荷直線

この直線は、Ep=400V，Ip=0mAとEp=0V，Ip=24mAを結んだ直線になっています。このときの負荷抵抗はRp=400V/24mA=16.7kΩ(16700Ω)となります。負荷抵抗はオームの法則に従います。また、プレートに流れる電流と負荷抵抗に流れる電流は等しいので、負荷抵抗にかかる電圧ELと流れる電流Ipの関係はIp〔A〕×16700Ω=EL〔V〕が成立します、プレートにかかる電圧Epと負荷抵抗にかかる電圧ELの合計が400Vですので、プレートにかかる電圧Epと流れる電流Ipの関係はEL+Ep=400とIp×16700=ELより、Ip×16700+Ep=400となります。これを変形すると、Ip=(400-Ep)/16700=-1/16700×Ep+0.024となります。これが、上の図で引いた負荷直線のグラフの式になります。

実際の設計の場合は、まず電源電圧を決めます。上の例の場合、400Vとなります。

ここで、グリッドの電圧を、次の図のように5Vを中心として10Vの振幅で振ってみると、EpとIpはこの直線の上を動きます。Eg=0VのときEp=130Vとなり、Eg=10VのときEp=250Vとなるのがわかります。よって、Egを10Vだけ振ることで、Epは120Vだけ増減します。Ipで考えると、Eg=0VのときIp=16.5mAとなり、Eg=10VのときIp=8.5mAとなります。よって、Egを10Vだけ振ることで，負荷抵抗に流れる電流(プレートに流れる電流)は8mAだけ増減します。負荷抵抗の値はRp=16.7kΩですので、負荷抵抗の電圧の増減は8mA×16.7kΩ=133Vとなります。どちらの場合もだいたい合っているのが分かると思います。入力された電圧の増減の幅が10Vで、負荷抵抗に現れる電圧の幅がだいたい120V〜133Vとなるので、増幅度(増幅率とは違います)は12〜13倍となります。

図．グリッド電圧Egを0Vから10Vまで振った時のプレート電流Ipの変化

このときのカソード抵抗も計算しておきましょう。増減の中心(入力信号の振れ幅がない時)を見ると、Eg=-5VのときIp=12mAですので、5V/12mA=417Ω≒420Ωをカソード抵抗として設定すれば、プレート電流12mAがカソードにも流れ、これにカソード抵抗420Ωを掛けた5Vがグラウンドとカソードの電位差になります。入力信号の振幅が0Vなので、グリッドに入力される電圧はグラウンドと同じ0Vとなり、カソードに比べるとEg=-5Vとなって、つじつまが合うことが分かります。

こっやって設計した増幅回路を下の図に示します。実際には、420Ωや16.7kΩのような抵抗のぴったりの値が存在しない場合が多いので、これらに近い抵抗の値を使うことになります。

ただし、上の負荷直線のグラフは、カソード電圧を0Vとしてプレート電圧とグリッド電圧を示したものです。カソードに抵抗を入れてバイアスを調整するカソードバイアスの場合には、カソードより、カソード抵抗にかかる電圧の5Vだけ下をグラウンド電位としていますので、上のカソードを基準としてプレートの電圧を測って計算している負荷直線とはプレート電圧が変化し、負荷直線が下に移動します。特に、負荷直線の端から端まで使って、なるべく増幅度を稼ごうとすると、グリッド電圧が0Vから-30Vまで変化することになりますので、実際の負荷直線は上の図とは結構ずれてしまいます。カソードバイアス回路の場合には、この設計法はあくまで大まかなものだと考えてください。

参考文献：笹尾利男，真空管工学，三共出版，1965年．