複雑な立体もスライスすれば簡単に！ 中学受験の面白い問題を紹介します！⑪

みなさん、こんにちは！
現役東大生ライターの松岡頼正です。

この連載では中学入試の面白い問題を、詳しい解説込みで紹介しています。

前回の記事はこちらです。

今回は算数の、立体図形の問題です。

ちゃんと図形問題を扱うのは初めてですね。

それではさっそく、こちらをご覧ください。

・問題

2024年度 東大寺学園中学 算数 3番より

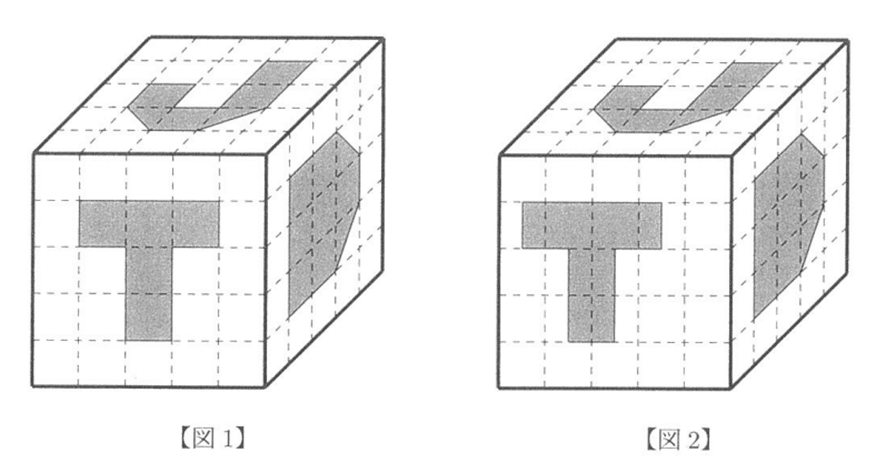
中学受験の算数ではよく見かける、立体をくり抜く問題ですね。
 
ToDaiJi（東大寺）の問題だけあって、くり抜く模様はTとDとJになっています。
 
立体図形の問題は、頭で図をイメージするのが難しいため、苦手な人もいると思います。
 
さらに立体をくり抜くとなると、すごく複雑な操作になりますよね。
 
そのため、いきなり全体を考えるのではなく、小さなパーツに分解して考えると見通しがよくなります。
 
今回の場合は、立体図形を一段ずつスライスして、上から順番にくり抜く部分を考えていくといいでしょう。
 
では、さっそく(1)から解いていきましょう！

(1)

今回は上から順に1段目、2段目…と考えていきます。

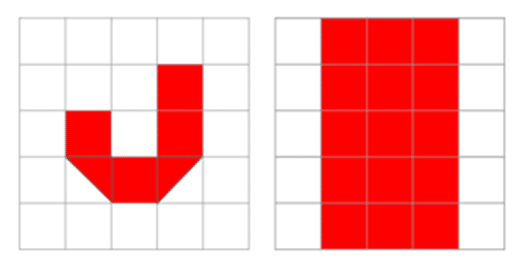
まずは、上の面のＪを考えましょう。
 
1段目から5段目のくり抜く部分を赤色で示した場合、このように同じＪの形が続くのが分かります。

次に、前面のTの字をくりぬいてみましょう。
 
1段目にはTの字がかかっていないので先ほどのJの時と変わりませんが、2段目にはTの横棒3マス分がくり抜かれます。
 
したがって、1段目と2段目は以下のようになります。

次に3段目と4段目ですが、Tの縦棒があるため、先ほどのJとくり抜く部分が重なります。

5段目は1段目と同じくTの字がかかっていないので、Jの形のままですね。
 
したがって、3～5段目は以下のようになります。

最後に、右の面にあるDの字のくり抜きを考えていきます。

これまでと違ってDの字には三角形でくり抜く部分もあるため、そこをオレンジ色にして示すと、1～2段目は以下のようになります。

1段目はDの字がかかっていないので、Jの形のままですね。

2段目はもともと真ん中の3列全体がくり抜かれているため、三角形にくり抜かれる部分は図のオレンジ色のところだけです。

次に3段目ですが、ここはDの字の真ん中の3マス分がズバッとくり抜かれるので、このようになります。

4段目はまたDの字の三角形にくり抜く部分があります。

5段目はDの字がかかっておらずJの形のままなので、それぞれ図にすると以下のようになります。

ということで、最終的にくり抜かれるのは、以下の赤色とオレンジ色の部分ですね。

「くり抜いた後に残る立体の体積を求めよ」という問題なので、オレンジ色（体積を半分として計算する）と白色の部分を合わせて計算すればいいですね。

まず1段目と5段目は、それぞれ全体で25マスのうち、赤い部分が合計で5マス分ずつあります。

マスの1辺が2cmなので、白い部分の体積は20マス×2段分ということで、
20×2×2×2×2＝320cm³ ですね。

次に2段目ですが、白が4マス、オレンジが2マスあります。

オレンジは体積を半分として考えるので、実質白が5マス分ということで、5×2×2×2＝40cm³ です。

3段目は白が8マス分なので、8×2×2×2＝64cm³ です。

4段目は白が8マス、オレンジが3マスあります。

したがって、白の部分の体積は8×2×2×2＝64cm³、オレンジの部分は3/2×2×2×2＝12cm³となります。

これらを合計した、320＋40＋64＋64＋12＝500 cm³ が(1)の答えですね。

(2)

では、(2)へ移りましょう。