【現役東大生が解説】中学受験の面白い問題を紹介します！①

みなさん、こんにちは！
現役東大生ライターの松岡頼正です。

みなさんは中学受験（以下、中受）の問題ってどんなイメージがありますか？

例えば国語の問題の文章がメチャクチャ長い、算数では高度な発想が求められる、社会や理科でものすごく細かい知識が要求される…など。

「とにかく難しい」という印象が強いかもしれません。

実際難しいのは確かなのですが、中には知的好奇心や想像力が刺激されるような、優れた問題もたくさんあるんです。

僕は実際に中受の勉強をしていて、そんな問題にたくさん出会いました。

中受を経験しない人も多いでしょうが、そんな良問が解けた時の楽しさを知らないままでいるのは、非常にもったいないんじゃないかと思います。

そこで今回から不定期連載で、中受の面白い問題を詳しい解説込みで紹介していきます！

一見すると難しそうな問題に対して、東大生がどんな思考回路でスムーズに解答までたどり着くのかを、分かりやすくお見せしていきます。

僕と一緒に、中受の問題の世界を楽しんでいきましょう！

・1問目（西大和学園・算数）

2023年度 西大和学園中学校（東京・東海・岡山会場）入試問題より

さて、さっそくこちらの問題を見てみましょう。手始めに、計算の問題からです。

「えっ、計算？」と拍子抜けした方もいるかもしれません。でも、こんな問題でも奥が深いんですよ。

一見すると複雑そうな計算ですが、あるコツを使えば1分で解けてしまうんです。そろばんなどの特殊な計算能力も必要ありません。

では、この問題を僕を一緒に解いていきましょう。
 
まず、この式の赤字にしたところに注目してみてください。

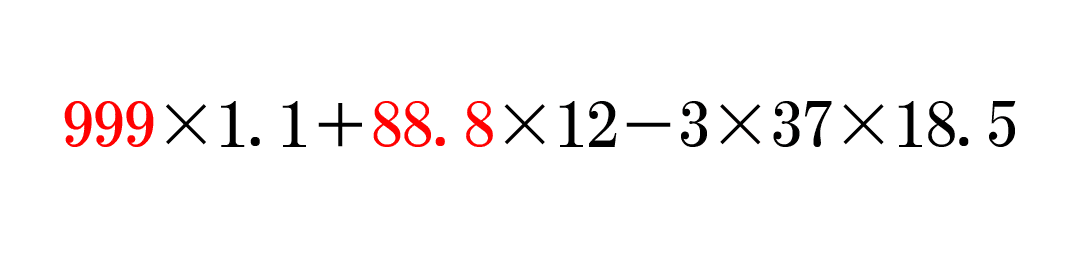
小数点の有無の違いはありますが、両方とも3ケタでゾロ目になっていますね。

これを見て「分配法則が使えそうだな」と気づいた方、正解です。
 
分配法則とは、以下のような計算で（　）を外しても結果が同じになる決まりのことです。 

( a + b ) × c ＝ a × c + b × c
a × ( b + c ) ＝ a × b + a × c 

例えば、(4 + 6) × 10 という計算を（　）から先にしたら、10 × 10 = 100 になりますね。

これに対し、(4 + 6) × 10 の（　）の中身にそれぞれ ×10 をして、4 × 10 + 6 × 10 = 40 + 60 としても、答えは100で同じです。
 
これを利用して計算を楽にできるように、まず 999 × 1.1 ＋ 88.8 × 12 のところを、こんな風に変形してあげます。

こうすれば、赤字のところで共通してかけられている111を（　）でくくることができるので、

   111 × 9 × 1.1＋111 × 0.8 × 12
= 111 × ( 9 × 1.1＋0.8 × 12 )
= 111 × ( 9.9＋9.6 )
= 111 × 19.5

と、式をスッキリさせることができます。
 
ここでもう一度、元の式を見てみましょう。

下線の部分は先ほど「111 × 19.5」の形まで整理できましたが、後ろの「－3 × 37 × 18.5」はまだゴチャゴチャしていますね。
 
実はここも111を使って下線部分と一緒に処理できるんです。
 
「3 × 37」のところを見てください。これ、答えはいくつでしょうか？

そうです、111になりますよね。
 
ということで、先ほどと同じように111で式全体を（　）でくくれるんです。 実際にやってみましょう。

　999 × 1.1 ＋ 88.8 × 12 － 3 × 37 × 18.5
 
= 111 × 9 × 1.1＋111 × 0.8 × 12－111 × 1 × 18.5
（分かりやすくするため 3 × 37 の結果を 111 × 1 と書いています） 

= 111 × ( 9 × 1.1＋0.8 × 12－1 × 18.5 )
 
= 111 × ( 9.9＋9.6－18.5 )
 
= 111 × ( 19.5－18.5 )
 
= 111 × 1 

いかがでしょうか？

あんなに複雑そうだった計算が、驚くほどシンプルな形になりましたね。
 
こんな風に計算のコツが分かると、簡単に解くことができるんです。マジックの仕掛けを見抜けたような感じがして、楽しくないですか？

試しにこのステップを踏んで、もう一度最初から計算してみてください。ちゃんと1分、少しかかっても2分以内には解けるはずです。 

中学受験の算数の問題はこのような計算問題から始まることが多いですが、後にひかえている難しい問題に時間を割くために、なるべく早くポイントを見抜いて処理してしまいたいところですね。

では、似たような計算問題をもう一問解いてみましょう。