
【力学】 3つのケプラーの法則の導出
2025/2/15 更新
この宇宙に存在する天体 (特に, 恒星と惑星) は, このKepler則に従って運動している. それを, 導出していきたい.
Keplerの第1法則:
惑星の運動は, 楕円軌道を描く.
Keplerの第2法則:
(中心力 $${F(r)}$$ まわりの) 面積速度は時間に依らず一定になる.
Keplerの第3法則:
$${T^2\propto a^3.}$$
($${T}$$ : 軌道周期, $${a}$$ : 軌道半径)
1. Keplerの第1法則の導出
§1. 万有引力から始める
前提として, 万有引力の法則は, 実験事実として既知とする$${^{*1}.}$$

$$
\tag{1.1}F(r)=-G\frac{mM}{r^2}
$$
なお, $${G}$$ は万有引力定数, $${m, M}$$ は2つの質点それぞれの質量, $${r}$$ は2つの質点同士の距離である. その上で, まず (2次元) Newton方程式を極座標表示するところから始める.
$$
\tag{1.2}
m\ddot{\textbf{\textit{r}}}=\textbf{\textit{F}}
\Leftrightarrow
m\begin{pmatrix}
\ddot{x} \\
\ddot{y}
\end{pmatrix}
=F(r)
\begin{pmatrix}
\cos\theta \\
\sin\theta
\end{pmatrix}
$$
ここで, 位置ベクトル $${\textbf{\textit{r}}}$$ について, 速度ベクトルを求めると,
$$
\textbf{\textit{r}}=
\begin{pmatrix}
x \\
y
\end{pmatrix}
=r
\begin{pmatrix}
\cos\theta \\
\sin\theta
\end{pmatrix}
$$
$$
\tag{1.3}
\dot{\textbf{\textit{r}}}=
\begin{pmatrix}
\dot{x} \\
\dot{y}
\end{pmatrix}
=\begin{pmatrix}
\dot{r}\cos\theta-r\dot{\theta}\sin\theta \\
\dot{r}\sin\theta+r\dot{\theta}\cos\theta
\end{pmatrix}
$$
となる. さらに加速度ベクトルは,
$$
\tag{1.4}
\begin{cases}
\ddot{x}=\ddot{r}\cos\theta-2\dot{r}\dot{\theta}\sin\theta-r\ddot{\theta}\sin\theta-r\dot{\theta}^2\cos\theta \\
\ddot{y}=\ddot{r}\sin\theta+2\dot{r}\dot{\theta}\cos\theta+r\ddot{\theta}\cos\theta-r\dot{\theta}^2\sin\theta
\end{cases}
$$
ここで, (1.2) より, 両辺 $${\cos\theta}$$ 倍したり, $${\sin\theta}$$ 倍したりして, 結局
$$
\begin{cases}
m\ddot{x}\cos\theta+m\ddot{y}\sin\theta=F(r) \\
m\ddot{x}\sin\theta-m\ddot{y}\cos\theta=0
\end{cases}
$$
というように, $${F(r)}$$ の寄与を片方の式だけに分離できる. そして, ここに (1.3) を代入すれば,
$$
\tag{1.5} \therefore m(\ddot{r}-r\dot{\theta}^2)=F(r)
$$
$$
\tag{1.6} \therefore 2\dot{r}\dot{\theta}+r\ddot{\theta}=0.
$$
前者 (1.5) は $${r}$$ 方向の, 後者 (1.6) は $${\theta}$$ 方向のNewton方程式をそれぞれ表していると考えられる$${^{*2}}$$. (1.6) より, 両辺 $${r}$$ 倍すれば,
$$
\frac{d}{dt}(r^2\dot{\theta})=0
$$
$$
\tag{1.7}
\therefore
r^2\dot{\theta}(=const.)\equiv h.
$$
よって, (1.1), (1.5), (1.7) より, $${u (\equiv \frac{1}{r})}$$ に対する微分方程式
$$
\frac{d^2u}{d\theta ^2}+u=\frac{GM}{h^2}
$$
が得られる. これの一般解は任意定数 $${A, \theta_0}$$ を用いて$${^{*3 },}$$
$$
\tag{1.8}
u=A\cos(\theta-\theta_0)+\frac{GM}{h^2} (0\leq A)
$$
で与えられる.
脚注
$${^{*1}}$$係数にマイナスがついているのは, 引力だからである. 片方の質点を座標の原点にとっているので, 原点に向かう向きは位置ベクトルにおいて, そのマイナスの向きで表される.
$${^{*2}}$$右辺が力の項と考えられるので, 中心力 $${F(r)}$$ が含まれる (1.5) は $${r}$$ 成分, 力が働いていない (1.6) は $${\theta}$$ 成分と解釈できるということ.
$${^{*3}}$$定数が2つ必要なのは, ( $${u}$$ の) 2階微分方程式を解く (積分する) ときに, 2つの積分定数 (自由度) が出てくるため.
§2. 2次曲線
(1.8) より, $${r=\frac{1}{u}}$$ に代入して,
$$
\tag{1.9a}
\therefore r=\frac{l}{1+\varepsilon\cos(\theta-\theta_0)}\\
l\equiv \frac{h^2}{GM}, \varepsilon \equiv \frac{h^2A}{GM}
$$
と求まる. これは, 2次曲線の曲座標表示であり, 離心率 $${\varepsilon}$$ について,
$$
\tag{1.9b}
\begin{cases}
\varepsilon=0 : 円\\
0<\varepsilon< 1 : 楕円\\
\varepsilon=1 : 放物線\\
1<\varepsilon : 双曲線
\end{cases}
$$
と場合分けできる$${^{*4.}}$$ ここで, (万有引力における) 力学的エネルギーについて,
$$
\tag{1.10}
\begin{equation*}
\begin{split} E &=\frac{1}{2}m\dot{\textbf{\textit{r}}}^2-G\frac{mM}{r} (\because -\frac{d}{dr}(-\frac{GmM}{r})=F(r))\\
&=\frac{m}{2}(\dot{r}^2+r^2\dot{\theta}^2)-G\frac{mM}{r} (\because (1.3))\\
&=\frac{m}{2}(\dot{r}^2+\frac{h^2}{r^2})-G\frac{mM}{r} (\because (1.7)より, \dot{\theta}の消去)\\
&=\frac{m}{2}\{(\frac{\varepsilon l\dot{\theta}\sin(\theta-\theta_0)}{(1+\varepsilon\cos(\theta-\theta_0))^2})^2+\frac{h^2}{l^2}(1+\varepsilon\cos(\theta-\theta_0))^2\}-\frac{GMm}{l}\{1+\varepsilon\cos(\theta-\theta_0)\} (\because (1.9a))\\
&=\frac{m}{2}\frac{h^2}{l^2}\{\varepsilon^2+1+2\varepsilon\cos(\theta-\theta_0)\}-\frac{h^2m}{l^2}\{1+\varepsilon\cos(\theta-\theta_0)\} (\because (1.7)と(1.9a)よりGMを消去)\\
&=\frac{mh^2}{2l^2}(\varepsilon^2-1)
\end{split}
\end{equation*}
$$
と書ける.
脚注
$${^{*4}}$$このことは, 例えば[2]を参照. また, (長半径 $${a}$$, 短半径 $${b}$$, 焦点 $${(\pm c, 0)}$$ の) 楕円の場合, $${l=\frac{b^2}{a}, \varepsilon =\frac{c}{a}}$$ となる.
§3. 恒星に束縛されるための条件
(質量をもつ) 質点同士が互いに万有引力で束縛$${^{*5}}$$されるためには, 常に $${E<0}$$ とならなければならない.

よって, (1.10) より,
$$
\varepsilon^2-1<0 \\
\therefore 0\leq\varepsilon <1
$$
となり, これは (1.9b) より (円も含む) 楕円軌道になることを示している. これを, Keplerの第1法則$${^{*6}}$$という.
脚注
$${^{*5}}$$互いの重力を振り切り, 無限遠方まで飛んでいって2度と帰ってこないというようなこと (散乱) が無いということ.
$${^{*6}}$$楕円軌道の法則ともいう.
2. Keplerの第2法則の導出
§1. 面積速度
次に, 楕円軌道における面積速度というものを考える. それは, 単位時間 $${dt}$$ あたりの2質点が通過した領域を囲む面積 (変化) のことで, 次のようになる$${^{*6}}$$.
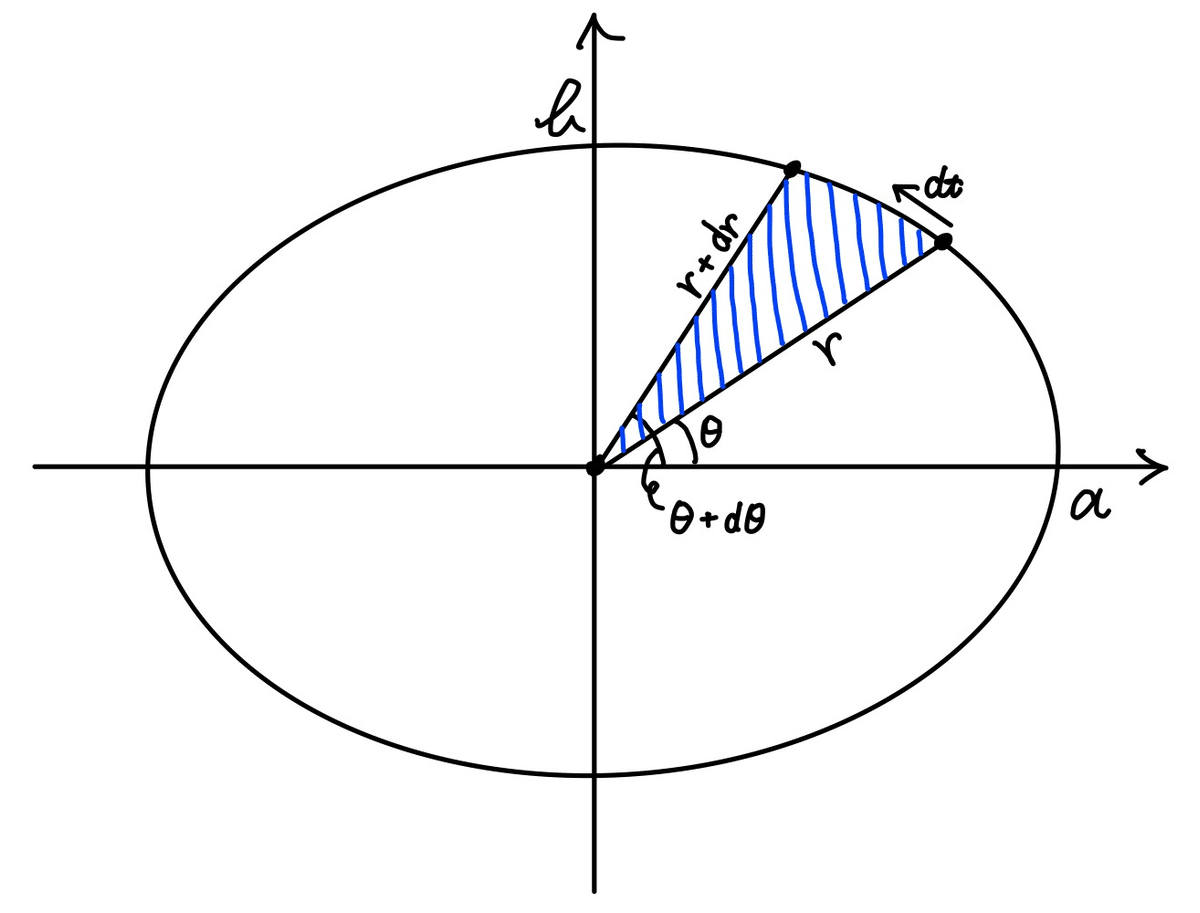
$$
(\text{斜線領域の面積})=\frac{1}{2}r^2d\theta
$$
あとは, これの両辺を $${dt}$$ で割れば,
$$
(\text{斜線領域の面積速度})=\frac{1}{2}r^2\dot{\theta}=\frac{h}{2}=const.
$$
というように面積速度が一定になることが分かる. これをKeplerの第2法則$${^{*7}}$$という.
脚注
$${^{*6}}$$微小量の2次項は無視している.
$${^{*7}}$$面積速度一定の法則ともいう.
§2. 角運動量保存則でもある
ちなみに, この2質点系には外力は働いていないので, 角運動量保存則$${^{*8}}$$が成立する.
$$
L=|\textbf{\textit{r}}\times(m\dot{\textbf{\textit{r}}})|=rmv\sin\frac{\pi}{2}=rmrd\theta (\because v=rd\theta)
$$
$$
\tag{2.1}
\therefore \frac{dL}{dt}=mr^2\dot{\theta}=2mh=const.
$$
よって, Keplerの第2法則は, 角運動量保存則の1種であることが分かる$${^{*9}.}$$
脚注
$${^{*8}}$$Newton方程式から導出できる. 詳細は, [1]などの力学の教科書やヨビノリさんの動画を参照して欲しい.
$${^{*9}}$$(2.1) において, $${\frac{dL}{dt}=const.(=0)}$$ であっても, 質量 $${m}$$ が時間変化する場合は $${h=const.}$$ となるとは限らない. しかし, 角運動量保存則自体は質量が変化しようがしまいが成立するので, そういう意味で第2法則よりも広い概念であると言える.
3. Keplerの第3法則の導出
§1. 軌道周期
楕円軌道における周期 $${T}$$ は, 楕円の面積 $${\pi ab}$$ を面積速度 $${\frac{h}{2}}$$ で割れば得られ,
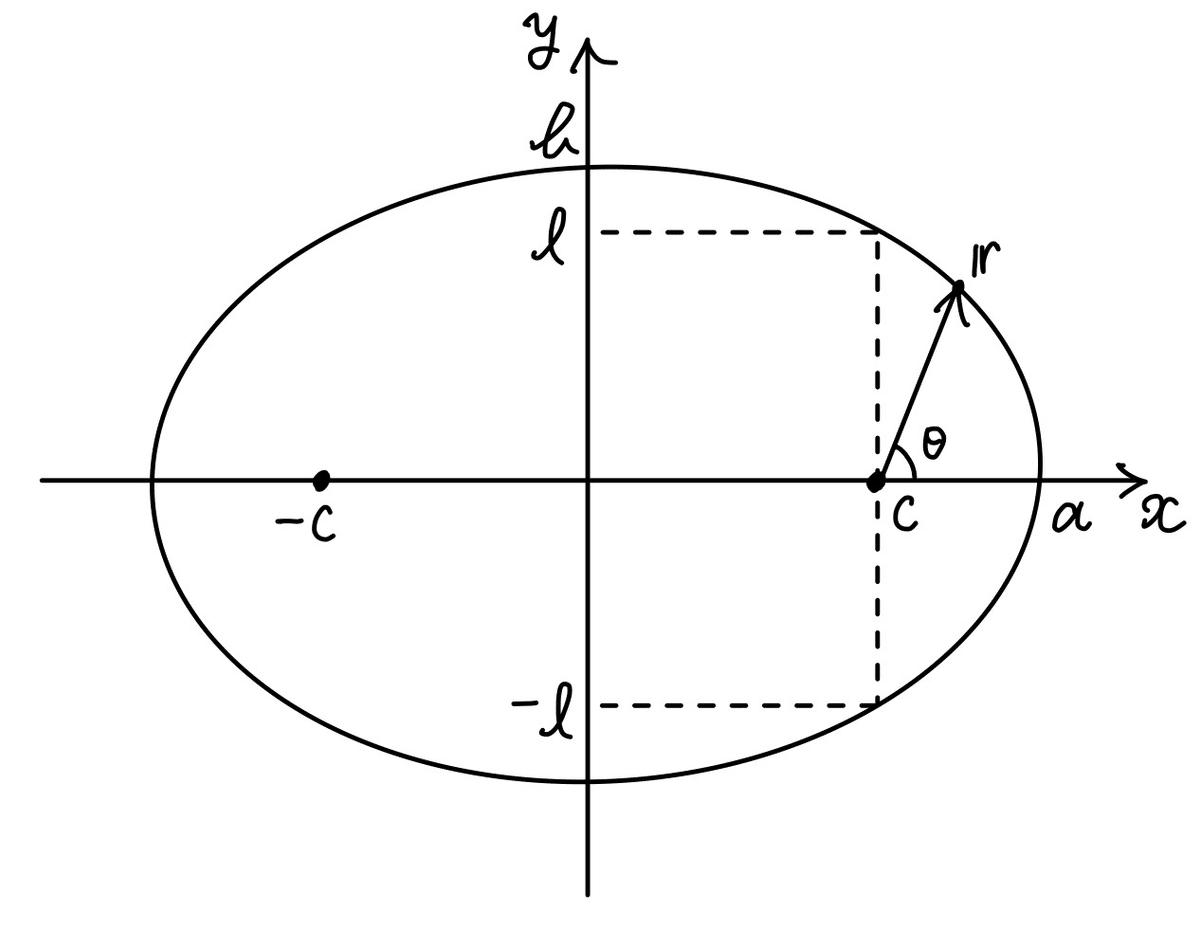
$$
T=\frac{\pi ab}{\frac{h}{2}}=2\pi \sqrt{\frac{a^3}{GM}}
$$
ここで, (1.9a) より, $${b, h}$$ について
$$
b=a\sqrt{1-\varepsilon^2}=\sqrt{al}\\
h=\sqrt{GMl}
$$
となることを用いている. 結局,
$$
\tag{3.1} \therefore T^2=\frac{4\pi^2}{GM}a^3 (\propto a^3)
$$
というKeplerの第3法則$${^{*10}}$$が導かれる$${^{*11}.}$$
脚注
$${^{*10}}$$調和の法則とも呼ばれる.
$${^{*11}}$$なお, 天体の場合, 恒星は焦点 $${(\pm c, 0)}$$ に位置すると考えられ, そこが原点Oである. そのため, 上図の中心にはOを明記しなかった. なお (1.9a) より, 新円に近づくほど $${c\rightarrow 0}$$ となる.
4. 参考文献
[1] 戸田盛和.『力学』新装版 (岩波書店, 2017).
[2] マスオ. "二次曲線(楕円,放物線,双曲線)の極座標表示". (高校数学の美しい物語, 2023).
