片持ち梁(1D)の変位
片持ち梁の変位の計算を行います。
Code_Aster & Salome-Meca 日本語解説に掲載されていたPOU_D_E要素の説明資料とページに掲載されていた解析データ(*.med,*.comm)を使い、動作を確認しました。
<記事作成時環境>
Salome-Meca 2018 for Windows
<動作確認環境>
Salome-Meca 2018 for Windows
Salome-Meca 2019 (OS :ubuntu18.04 , CAELinux2020Lite)
1.解析の概要
片持ち梁のたわみをビーム要素で計算する。

棒の幅:0.02m、高さ:0.002m、長さ0.1m
材料:ヤング率210GPa、密度7830kg/m^3
荷重:10N(-Z方向)
要素:ビーム要素(POU_D_E要素、ベルヌーイ・オイラー梁)
せん断を考慮しない材料力学の公式で使うものです。
2.計算結果
変位(DEPL):-0.001190mm
曲げ応力最大(SMFY):75MPa(75000000Pa)
<変位>
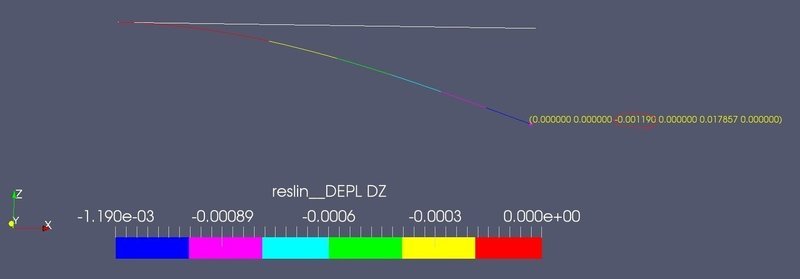
<曲げ応力>

3.検算
片持ち梁のたわみと曲げ応力公式から検算をします。
(1)荷重位置のたわみδ
δ = P x L^3 / 3 x E x Iy
P:荷重(N)、L:長さ(m)、Eヤング率(Pa)、
Iy:断面2次モーメント(y軸回り)(m^4)
δ= 10 x 0.1^3 / { 3 x 2.1 x 10 ^11 x 1.333 x 10^(-11) } =
0.00119mm
(2)曲げ応力σx (はり上端位置)
今回の曲げモーメントの場合、はり上端(+z方向)位置の応力が最大になるため、曲げ応力(X方向の応力)は
σx = M / Iz x z
M:曲げモーメント(Nm)、Iy:断面2次モーメント(y軸回り)(m^4)
z:はり上端位置(今回長方形断面のため、高さ/2)(m)
σx = 10 x 0.1 / 1.333 x 10^(-11) x 0.001 = 75000000 Pa = 75MPa
4.その他
・普段は仕事でほとんど使わないため、確認はここまでにとどめます。
・今回、曲げ応力は、断面が長方形だったため、検算は問題なく終わりました。中立軸が断面高さ/2にならないL字型やT字型など断面形状で曲げ応力を計算する場合は、節点にかかる荷重とモーメントもあわせて確認することをお勧めします。(CALC CHAMPのFORCE上からFORC_NODA、REAC_NODAを追加)
・Kengo MEADA様におかれましては、貴重なデータを「Code_Aster & Salome-Meca 日本語解説」のWeb上へ公開いただきましたこと、お礼を申し上げます。
引用ページ:Code_Aster & Salome-Meca 日本語解説内 POU_D_E要素URL:https://sites.google.com/site/codeastersalomemeca/home/code_aster-1/bimu-youso/pou_d_e-youso
