
SalomeMecaによるヒータの非定常熱伝導解析
OpenCAE学会シンポジウム2023で実験とCAEのテーマで、本記事の解析事例をトレーニングを行いました。
トレーニングでは本記事のsalomemecaの解析操作、対象物のヒータの原理、測定の仕組みも開設しています。
数年前にという解析塾シリーズで実験とCAEの結果を検証した事例の本を読みいつか身近なものでできないだろうかと思ってて、やることができました。OpenCAE学会シンポジウム2023でトレーニングを行いました。
鋳込みヒータを用いて、ヒータの発熱による温度変化を測定し、併せて解析も行い比較をやってみました。
鋳込みヒータは、自宅にあった壊れかけた炊飯器のヒータを分解し取り出しました。

1.実験
1.1 概要
鋳込みヒータを直流電源により一定の発熱量を与えて、鋳込みヒータの温度変化を調べました。
使用電圧:①DC5V、②DC12V(パソコンの12V電源、5V電源を使用)
試験時間:30分(温度が一定付近とみなせるまで)
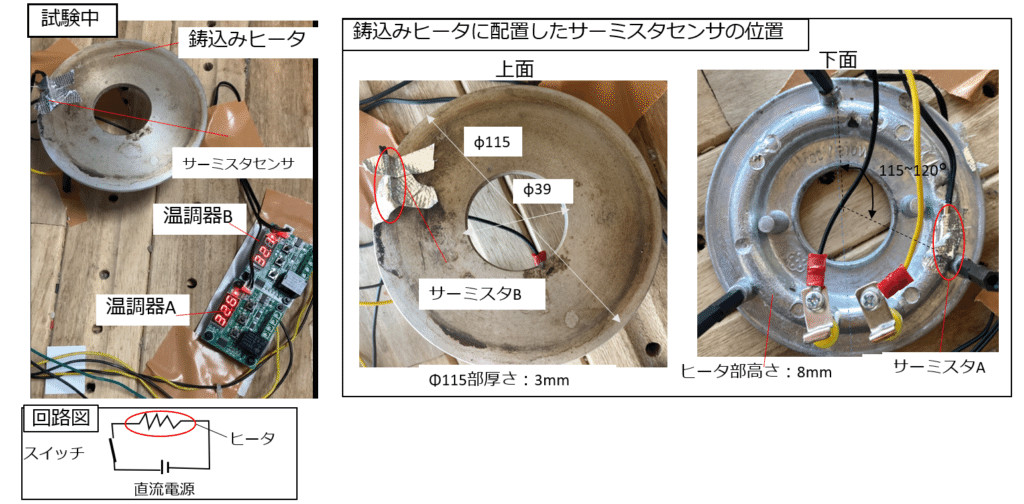
温度センサ:サーミスタセンサ2ケ所(鋳込みヒータに背面に配置)
温調器AはサーミスタAの温度、温調器BはサーミスタBの温度を表示温度の記録:温調器A、温調器Bの値を1分おきに読み取る
ヒータ周囲の環境:自然対流(周囲を扇風機等で空気を攪拌していない)
1.2 実験結果
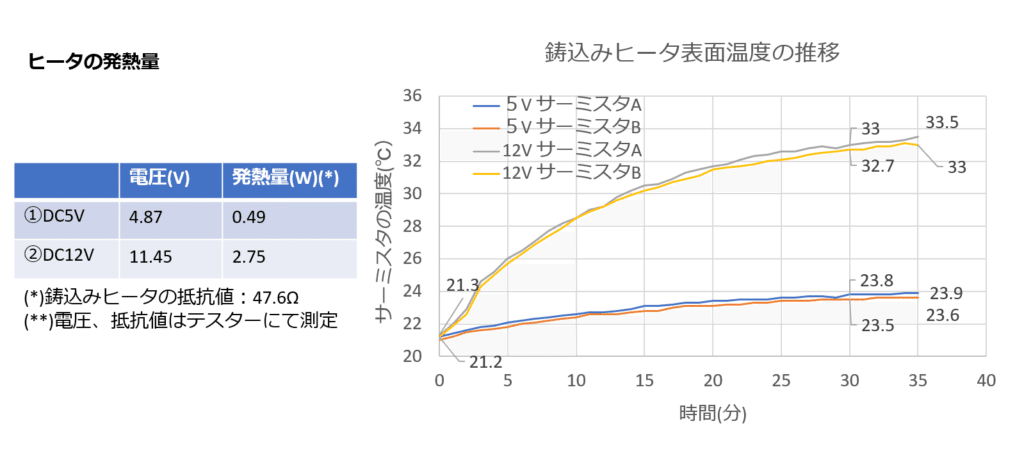
上図が実験結果となり結果を考察していきました。
鋳込みヒータはほぼ均一な温度になっていた。サーミスタAはシーズヒータの外側、サーミスタBはその裏側に配置したため温度差がでると予想したが、ほぼ均一という結果でした。
鋳込みヒータの表面温度は、両条件ともに30分を超えるとほぼ一定になっていた。
2.解析
ヒータの表面温度の時間推移が実験と近い結果になるかSalomeMecaにて解析を行いました。
2.1 解析概要
鋳込みヒータのモデルを3DCADにて作成し、非定常伝熱解析を行いました。
・使用環境:SalomeMeca2019(VirtualBox+CAELinux),OS:windows11
・解析対称:鋳込みヒータ
・メッシュ:四面体1次要素
・拘束条件:シーズヒータ部一様発熱、ヒータ外径面:熱伝達率で同一設定
・温度:サーミスタA位置の表面温度
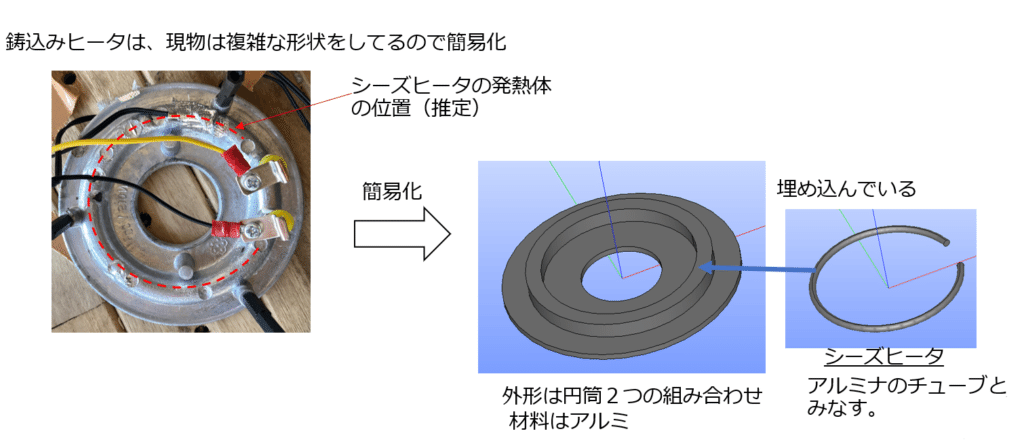
・解析モデル:図4に示すように簡易化を行っています。
熱伝導率(W/m2):アルミナ35、アルミ200
比熱(J/kg/K):アルミナ800、アルミ900
密度(kg/m3):アルミナ3900、アルミ2700
条件1
ヒータ発熱量2.75(W)、熱伝達率8.41(W/m2/K)
条件2
ヒータ発熱量0.498(W)、熱伝達率6.35(W/m2/K)
熱伝達率は、形状や対象となる物体の表面の対流形態で決まる係数です。ここでの解析は、平板の熱伝達率(横置き)の計算式を用いました。計算は、下に示すページから計算を行いました。
仮定条件として、代表長さをヒータ外径115mm、初期温度はヒータの初期温度21.2℃とし、条件1は25℃時の結果、条件2は35℃時の結果を使用しました。
平板の熱伝達率の計算(自然対流熱伝達) | 科学技術計算ツール (cattech-lab.com)
2.2 解析結果
(1)実測との比較
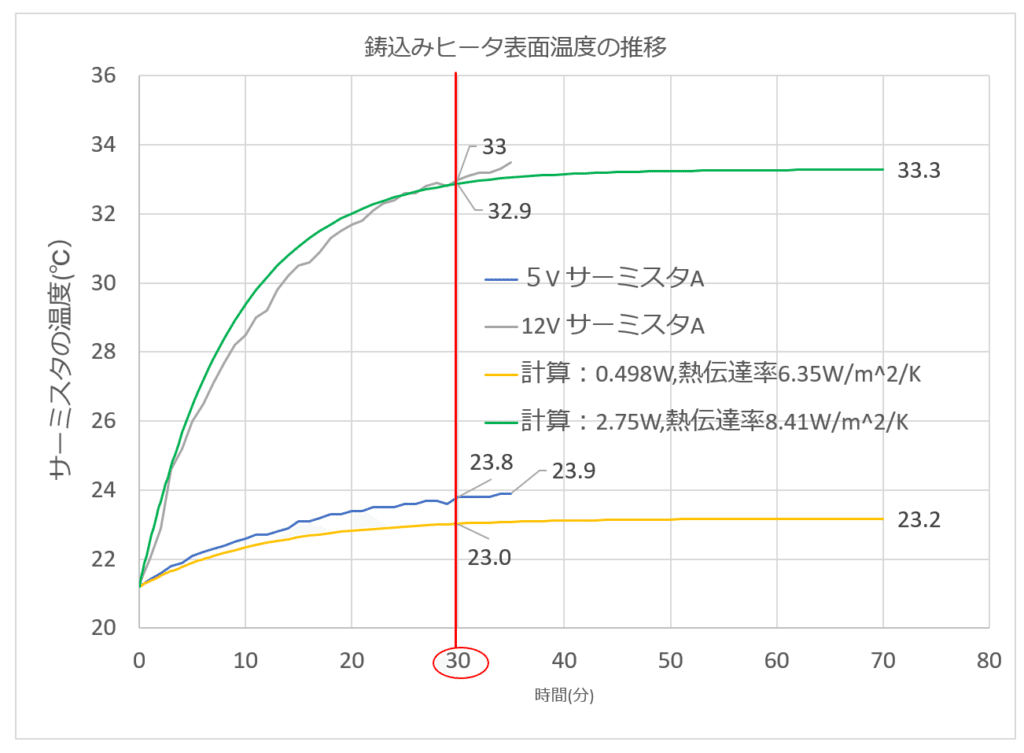
30分程度の位置で比較を行いました。条件2は実験に対して低い傾向にありました。
条件1…実験33℃、計算32.9℃
条件2…実験23.8℃、計算23℃
グラフの数値は、インターネット上にParaviewから数値を取り出す事例が掲載されていたため、この事例を用いてParaview上からcsvデータに変換を行いました。
openFoamを用いてある点の各種量の時系列データを出力させる方法 - niodachiが現場所長になるまで日記 (hatenablog.com)
(2)ヒーター表面温度の推移
条件1
条件2
3.まとめ
非定常熱伝導解析を行い実験と比較をしました。
・ヒーター表面の温度変化は、実測と測定の結果が近い傾向結果が出ました。
・モデルの近似化はシーズヒータは体積の大半を占めるアルミナのチューブと仮定しても良好な結果でした。
・SalomeMecaへの熱伝達係数の入力は、温度と熱伝達係数の関数にすると、ヒーター表面の温度変化は現物に近くなると考えます。
・熱伝達率の情報が少なく、経験則による数値ではないかと推測していました。
本発表においては、第22回オープンCAE勉強会@関東(構造など)にご出席の方からコメントをいただきました。この場にてお礼申し上げます。
・実測の温度推移がまだ完全に落ち着いていないように見えるので、もう少し試験時間を延ばしたほうがよい。
・熱伝達係数の情報が少ないのは、実測と現物を合わせこんでるケースが多いため、解析対象となる物体の実験地になっている。
・熱伝達係数は、物体を鉛直に置いた場合と水平に置いた場合では空気の流れが違うので数値が違うため、前提条件を調べたほうがよい。(この記事内の計算は、この指摘を受けて熱伝達係数を選びなおしています)
・Openfoamやfluentのような解析で熱流体解析を行うと、よいかもしれないが現物との合わせこみは難しい。
数年前にという解析塾シリーズで実験とCAEの結果を検証した事例の本を読みいつか身近なものでできないだろうかと思ってて、やることができました。
4.補足資料
(1)commファイル
条件1の時のcommファイルです。
物性値は、熱伝導率(W/mm2/K)、比熱(J/mm3/K)、熱伝達率(W/mm2/K)に換算しました。
発熱量(soruce)は、単位体積当たりの発熱量を入力しました。(ヒータの体積はCAD上から算出し2985mm3)
DEBUT(identifier='0:1',
LANG='EN')
mesh0 = LIRE_MAILLAGE(identifier='1:1',
FORMAT='MED',
UNITE=2)
model = AFFE_MODELE(identifier='2:1',
AFFE=_F(MODELISATION=('3D', ),
PHENOMENE='THERMIQUE',
TOUT='OUI'),
MAILLAGE=mesh0)
almi = DEFI_MATERIAU(identifier='3:1',
THER=_F(LAMBDA=0.2,
RHO_CP=0.00243))
almina = DEFI_MATERIAU(identifier='4:1',
THER=_F(LAMBDA=0.036,
RHO_CP=0.00311))
fieldmat = AFFE_MATERIAU(identifier='5:1',
AFFE=(_F(GROUP_MA=('cast', ),
MATER=(almi, )),
_F(GROUP_MA=('heater', ),
MATER=(almina, ))),
MODELE=model)
timestep = DEFI_LIST_REEL(identifier='6:1',
DEBUT=0.0,
INTERVALLE=(_F(JUSQU_A=200.0,
NOMBRE=20),
_F(JUSQU_A=420.0,
NOMBRE=10),
_F(JUSQU_A=4200.0,
PAS=60.0)))
load0 = AFFE_CHAR_THER(identifier='7:1',
ECHANGE=_F(COEF_H=8.41e-06,
COEF_H_INF=8.41e-06,
COEF_H_SUP=8.41e-06,
GROUP_MA=('outer1', 'outer2', 'outer3', 'outer4', 'outer5', 'outer6', 'outer7', 'outer8'),
TEMP_EXT=20.0,
TEMP_EXT_INF=0.0,
TEMP_EXT_SUP=100.0),
MODELE=model,
SOURCE=_F(GROUP_MA=('heater', ),
SOUR=0.0001669))
resther = THER_LINEAIRE(identifier='8:1',
CHAM_MATER=fieldmat,
ETAT_INIT=_F(VALE=21.2),
EXCIT=_F(CHARGE=load0),
INCREMENT=_F(LIST_INST=timestep),
MODELE=model)
unnamed = CALC_CHAMP(identifier='9:1',
RESULTAT=resther,
THERMIQUE=('FLUX_ELGA', 'FLUX_ELNO', 'FLUX_NOEU')))
IMPR_RESU(identifier='10:1',
RESU=(_F(RESULTAT=resther),
_F(NOM_CHAM=('FLUX_NOEU', ),
RESULTAT=unnamed)),
UNITE=80)
FIN(identifier='11:1',
)
(2)DC5V,DC12V電源の供給方法
使わなくなったパソコン電源を使いました。インターネット上にパソコンから直流電源を作る方法があったので、その記事を見ながら作りました。安全に実験できるように端子台に圧着端子を用いて接続を行いました。

