
流体力学 等角写像(理論編)
皆様おはこんばんちは。
最近,流体力学を再度学び直してみようと思い,記事にしています。
第47回目は,「等角写像」について紹介していきます。なお,等角写像は理論編と例題編として記事にする予定です。また,2023年の書き始めなので,よろしくお願いします。
(1)等角写像とは
まず,「等角写像」について,解説していきます。
大学の数学をきちんと履修した人は問題なく導入できると思いますが,筆者のように履修はしたが,「問題が解けるだけ」で「線形代数・複素関数の理論がまったく分からない」という人向けに流体力学で使うことだけを優先して紹介します。簡単にまとめると,図1のような考え方だと筆者は思っています。(※細かい議論はできないのであしからず)

図1の解説を一個ずつ進めます。
まず,線形代数で取り扱う「線形写像」です。ユークリッド空間(理学部以外でこの空間が違う空間を使うことはまずないです)で関数が直線ならば,別のユークリッド空間に変換できることを「写像」と言います。ここで詳しい理論は省略します。
次に,複素関数で取り扱う「正則関数」です。詳しくは過去の記事を参考にしてください。
これらの理論を組み合わせると流体力学で使う「等角写像」です。2つの複素関数が「正則関数」であると,「別の平面(複素関数は2次元で扱うため)に変換する」と,2つの平面にできる微小図形の角度が同じになるため,相似な図形となります。そして,得られた別の平面に写像した複素ポテンシャルから流れの状態を求められます。
次項では,等角写像をしたときに「相似な図形」となることと別の平面に変換したときも「同じ複素ポテンシャル」となることを証明してみましょう。
(2)等角写像について(証明)
ここでは,等角写像の証明をしていきましょう。最終目標は「相似な図形」と「平面変換したときも同じ複素ポテンシャル」となる2点です。
まず,1点目の「相似な図形」を証明しましょう。図2のように2つの複素数z=x+iy,ζ=ξ+iηがあると仮定し,両者の関係が正則関数とするため,式(1)のようになります。

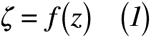
あとは図2に示したように,z平面上とζ平面上の2点の対応関係については式(2),式(3)のようになります。
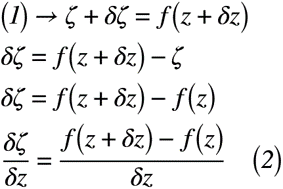

式(2)と(3)は,いずれも正則関数であることを証明できたことになります。微分の考え方と同様に微分の定義式が式(2)と(3)で記述できたので,あとは極限を追加します。なので,図2の図形をもとに考えると,PP1とPP2がそれぞれ限りなく零に近づくと,PP1とPP2が十分小さくなるので,式(4)のようになります。

ここで式(4)の関係が成立すると,式(5)のように記述できます。

よって,式(5)は分かりづらい形式ではありますが,中学3年で触れる「相似な図形」の証明となります。式(5)に示す通り,「2組の辺の比とその間の角がそれぞれ等しい」図形となるため,式(5)のような結論が導けます。
つまり,2つの複素数が正則である場合,z平面上の曲線をζ平面上に写しかえること(写像)が証明できました。
次に「平面変換したときも同じ複素ポテンシャル」であることを求めます。複素数zが正則である場合でかつ,z平面上の境界Kに写像した場合は,z平面で境界Kとする流れは式(6)のようになります。
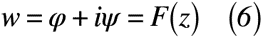
もし,複素数ζが正則である場合でかつ,ζ平面上の境界Kに写像した場合についても同様の考え方ができるので,式(7)のようになります。
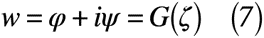
これにより,z平面からζ平面に変換したときも同じ複素ポテンシャルが得られることが証明できました。
では,この理論が何に有用なのかを紹介します。
それは,流れの状態がz平面上では直観的に求められない場合でも,ζ平面上に変換した関数を利用することで,「実質的にz平面上における境界Kとする流れの状態を求められること」です。つまり,関数で記述すると,合成微分の考え方が使えるため式(8)のように記述できます。
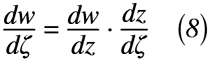
ここまでが等角写像に最低限必要な理論となります。次回の記事では,実際の流れの状態をどのように記述できるかを紹介します。
(3)まとめ
今回の記事のまとめを以下に示します。
(1)等角写像は,線形写像と正則関数を合わせた考え方である。
(2)等角写像の前提条件は,2つの複素数が相似な図形で平面変換しても
同じ複素ポテンシャルとなる。
以上です。最後まで閲覧頂きありがとうございました。
次回は,「等角写像(例題編)」について,解説する予定です。
いいなと思ったら応援しよう!

