流体力学　渦に関する法則

　最近，流体力学を再度学び直してみようと思い，記事にしています。
　第３３回目は，前回の予告通り「渦に関する法則」について紹介していきます。

（１）渦の何を取り扱うのか？

　 では，「渦に関する法則」について，解説していく訳ですが，筆者以外は，「何をそんなに取り上げる必要があるの？」と思うはずです。そこで，「渦に関する法則」として取り上げる内容を以下に箇条書きで示します。そして，各項目で記事にする予定ですので，興味のある分野や関連項目で見たいなどでいいかと思います。

（ⅰ）渦管を取巻く閉曲線Cで循環Γが成立するのか。
（ⅱ）2次元平面から3次元曲面でも循環Γが成立するのか。
（ⅲ）2次元流れの渦度は時間経過によってどう変化するのか。
（ⅳ）閉曲線Cに沿う循環Γは時間経過でどう変化するのか。

　基本的には，渦と取り扱うときに必ず登場する循環Γがどのようなモデルでも成立するのかをメインに取り扱います。今回は，「（ⅰ）渦管を取巻く閉曲線Cで循環Γが成立するのか。」について投稿していきます。

（２）渦管を取巻く閉曲線Cで循環Γが成立するのか。

（2-1）渦管とは？

　以前にも「渦度」の記事として取り上げました。以下の記事を参照してください。

　今回，少し復習すると，図1に示すようなモデルが渦管です。要するに，閉曲線Cや循環Γは，図1の緑色箇所で起きていると考えればよいのです。この渦管は，いわゆる渦線の断面のようなものなので，適当なところで切った断面で発生している渦の運動の様子を確認していると思ってよいのではないでしょうか。

図1　渦運動のモデル

　では，次項ではモデル化により渦管の断面で発生している渦運動の様子を確認するために，閉曲線Cと循環Γの関係を見ていきましょう。

（2-2）閉曲線Cと循環Γの関係

　それでは，図2に示すように渦管と取巻く閉曲線Ｃを考えてみましょう。イメージとしては，渦管の断面に循環Γが存在し，その周りを任意の閉曲線Ｃが沿うにようにあるモデルを想定します。

図2　閉曲線Ｃと循環Γのモデル

　ここで，図2に示してあるように，閉曲線Ｃ，Ｃ‘と循環Γに点Ａ，Ｂ，Ｃを配置しています。これを用いて，渦管を取巻く閉曲線Cで循環Γが成立するかを証明するのに利用します。
　では，証明していきます。2つの閉曲線の間には渦が存在しないとします。そして，2つの閉曲線を線分ABで結んで，起点をＡ→Ｃ→Ａ→Ｂ→Ｃ‘→Ｂ→Ａを結ぶ経路を循環Γとします。
　まずは，経路を仮に決めた循環Γを閉曲線C，C‘を経ることと，循環の定義を用いると，式（1）のように表せます。また，循環の定義については以前の記事で紹介していますので，確認してみて下さい。

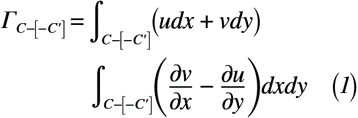
　次に，各経路（Ａ→Ｃ→Ａ→Ｂ→Ｃ‘→Ｂ→Ａ）を経た循環Γを考えると，式（2）のように表せます。

　よって，式（2）を式（1）に代入すると，式（3）のように表せます。

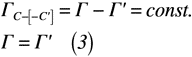
　これにより，閉曲線C，C‘の間に存在する循環ΓとΓ‘が同様となることが分かりました。つまり，渦を取巻く閉曲線Cの大きさが限りなく大きくなっても，小さくなっても循環Γ，Γ’は変化しないので，数値が変わらないことを意味します。
　循環Γの値が変わらないのは，非常に大きい意味を持ちます。なぜなら，一つの断面の循環Γの値が分かれば，他の循環Γ‘の値は求めるまでもなく，同じ値になることを意味しています。
　実際の研究・開発の現場などで登場する流れ場では，循環Γが一定であるのかは不明ですが，どうやっても循環を定量的に測定，計算できないとなれば，この理論をベースに進めることが出来るのです。

（３）まとめ

　今回の記事のまとめを以下に示します。
（１）渦に関する法則は，主に4つ取り上げる。今回は，（ⅰ）渦管を取巻く閉曲線Cで循環Γが成立するのか。
（２）循環は，閉曲線Cの内部，もしくは外部に沿うように発生する。
（３）閉曲線Cの大きさに関わらず，循環Γの値は変化しない。

　以上です。最後まで閲覧頂きありがとうございました。

※次回は，「渦に関する法則（その2）」について扱う予定です。