
流体力学 翼理論(その3)
皆様おはこんばんちは。
最近,流体力学を再度学び直してみようと思い,記事にしています。
第58回目は,「翼理論」について紹介したいと思います。今回は,その3として円柱,平板翼等の周りの流れについて取り上げたいと思います。
(1)一様流れの場合
今回は,円柱,平板翼等の周りの流れについて再度触れてから,本格的な議論に移ります。今までの記事で触れてきたことをここで軽くまとめますが,より詳しく知りたい方は,以下の記事を参考にしてください。
さて,円柱と平板翼等の周りの流れは式(1)に示すような,等角写像により半径aの円柱に速度u0の一様な流れがあたる場合は,図1のようなz平面からζ平面への変換が出来ます。

この式(1)を「ジューコフスキー変換」と呼び,特にz座標の原点近くの座標軸以外の1点を中心とする円をζ平面上に等角写像すると,翼形は「ジューコフスキー翼」として写像されます。

一方,半径aの円柱に速度u0の一様な流れがあたる場合の円柱の周りの流れの複素ポテンシャルwは,式(2)のように表されます。

また,式(2)を式(1)に代入すると,平板に平行に流れる流れの複素ポテンシャルwは,式(3)のように表されます。

ここまでが,一様流れにおける円柱,平板翼等の周りの流れの復習です。
(2)z平面のx軸に適当な傾き角αをなす一様流れの場合
次に取り上げるのは,z軸と適当な傾き角αをなす一様流れの場合を考えます。
先ほど,半径aの円柱に速度u0の一様な流れがあたる場合は,図1と式(2)で表されることを確認しました。今度考えるz平面のx軸に適当な傾き角αをなす一様流れの場合は,図2で表されることが既に知られていますが,感覚的にも分かるかと思います。ここで,適当な傾き角αで傾いた軸をそれぞれ,x’軸とy’軸とします。

図2から,x’軸方向に速度u0の一様な流れの中に円柱があるz’平面に対する複素ポテンシャルwは,式(4)のように表されます。

ここで,z’平面とz平面はαの傾きをなしているので,複素数z’は,複素数zを上手く変換しながら,式(5)のように考える必要があります。

よって,z平面における複素ポテンシャルwは,式(5)を式(4)に代入すると,式(6)のように表されます。

ここで,式(6)に含まれる複素数zを消去したいので,式(1)のジューコフスキー変換を式変形すると,2次方程式の解の公式となり,式(7)のようになります。このとき,z平面の半径aは必ず「+」となります。また,極限ととっても,z→∞のとき,ζ→∞に対応するため,zの値は「+」のみを考えれば良くなります。

よって,z平面上の半径aの円柱はζ平面上の長さ4aの平板に写像されるため,ζ平面上の流れは式(7)を式(6)へ代入すると,式(8)のようになります。

式(8)を見たときに,筆者を含めて多くの方々が「げんなり」したと思います。式(8)の状態では不完全なことが推察できますが,解くためのハードルが高そうです。そこで,式(8)のcosαとsinαについてそれぞれ解いたものを使って,式(8)を完全に解いていく方針を立てました。
まずは,cosαから解きます。以下のように展開して解くと,式(9-1)が得られます。

次は,sinαを解きます。cosαのときと同様に以下のように展開して解くと,式(9-2)が得られます。

最後に,式(9-1)と式(9-2)を式(8)へ代入すると,式(9)のように表されます。
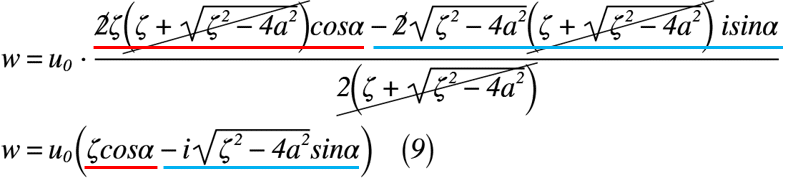
この式(9)こそ,流れを図示すると,図2のζ平面上のようになるそうです。
ここでもし,ζの値が十分大きな場合(ζ>>1),aの値の影響を受けず,ζの値を定数として考えられるので,式(9)は式(10)のように書き換えることが出来ます。このとき,ξ軸とαの傾きをなす,速度u0の一様な流れになります。

(3)z平面のx軸に適当な傾き角αをなす一様流れと循環を加えた場合
最後に取り上げるのは,z軸と適当な傾き角αをなす一様流れと循環を加えたの場合を考えます。このときの複素ポテンシャルwは,式(6)に循環(-Γ/(2πi)logez)を加えることで記述できるので,式(11)のように表されます。
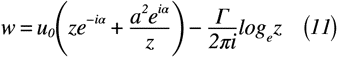
ここで,円柱周りの流速を考えると,複素ポテンシャルwを複素数zについて微分することで得られるので,式(12)のように表されます。

さらに,円柱周りの流速が「ゼロ」(u=v=0)と考え,2次方程式の解の公式を解くと,複素数zは式(13)のように表されます。

この式(13)の根号内を考えると,解は以下の3通りに考えることが出来ます。

そして,得られた解の3通りに沿って,半径aの円柱に速度u0のx軸に適当な傾き角αをなす一様流れと循環を加えた場合は,図3のように表されます。

次に,ζ平面における平板の周りの流れについて考えます。式(1)のジューコフスキー変換を式変形すると,複素数zは式(14)のように表されます。

よって,z平面の半径aの円は,ζ平面の長さ4aの平板に写像されるため,式(14)を式(11)に代入すると,式(15)のように表されます。

(4)まとめ
今回の記事のまとめを以下に示します。
① z平面における半径aの円は,ζ平面の長さ4aの平板に写像される。
② z平面のx軸に適当な傾き角αをなす一様流れの場合でも,z平面における半径aの円は,ζ平面の長さ4aの平板に写像され,±2aの2カ所によどみ点ができる。
③ z平面のx軸に適当な傾き角αをなす一様流れと循環を加えた場合,z平面における半径aの円周上に2カ所,1カ所,もしくは円の外側に1カ所のよどみ点が生じる。
以上です。最後まで閲覧頂きありがとうございました。
次回は,「翼理論(その4)」について,解説する予定です。
いいなと思ったら応援しよう!

