
流体力学 渦の層と渦列(その2)
最近,流体力学を再度学び直してみようと思い,記事にしています。
第43回目は,「カルマン渦列」を紹介する予定でしたが,「渦列」で紹介できていない部分がまだありましたので,「渦の層と渦列(その2)」と題して紹介していきます。
(1)渦列の共役複素速度
では,渦列の複素ポテンシャルの共役複素速度を算出してみましょう。以前の記事で,共役複素速度を求めるために必要な複素ポテンシャルは証明しております。
そこで得られた式を使いましょう。そのため,式(1)のように表せます。
![]()
今回は,直交座標系の共役複素速度を求めるので,式(2)のように計算を進めます。但し,zの位置は原点のため,z=0とします。また,隣に渦があることで渦列が動かされることを仮定したうえで,複素ポテンシャルを求めます。


式(2)の結果から,原点にある渦は「静止状態」であることが分かります。つまり,図1に示すように,他の渦によって,その場から移動したりはしないのです。ちなみに,他の渦も同様に「静止状態」となります。

図1 渦列の静止状態
(2)渦列の時間経過
次に紹介していくのは,前項と同様に,隣に渦があることで渦列が動かされることを想定することを仮定したとき,渦列が時間経過していくことでどのように変化するのかです。つまり,「渦列が僅かに変位するときの時間変化を知る」ことと同じになります。
そこで渦列の時間変化を知るには,前項の式(1)および式(2)と同様に複素ポテンシャルから共役複素速度を求めます。
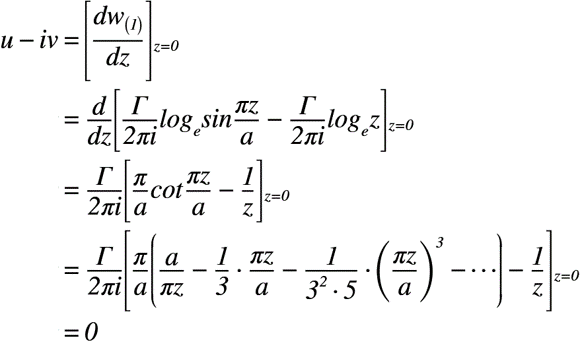
上式で得られた結果から,渦列がx,y方向にわずかに変化したときを想定するため,zが十分に小さいと仮定すると(数学的には,z<<1),共役複素速度のzの2次元項以降は,無視できるので,式(3)のように表せます。

ここで,式の置換を行って書き直し,,u=dx/dt,v=dy/dtとすると,式(4)のように表せます。

式(4)を時間tについて微分し,代入を行うと,式(5)のように表せます。この式がいわゆる大学数学の微分積分で取り扱う「2階定数係数斉次線形微分方程式」です。

よって,式(5)から一般解(係数A, B,λにどんな数値が代入されるかは不明だが,係数に数値代入をすれば,解が得られる状態になる解のこと)は,xおよびyの一般解は,式(6)のように表せます。
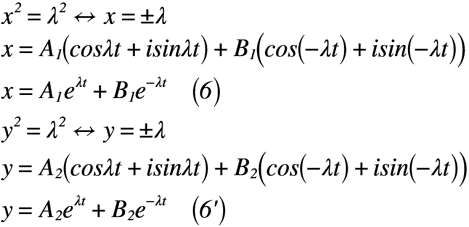
つまり,時間経過に伴って,xとyは増加していきます。その様子は,図2に示します。

図2 時間と変位の関係
この結果から,僅かに変位を受けた渦は,図3のように時間経過とともに平衡位置から離れていくため,渦列が不安定になっていくことが分かります。

図3 渦列の平衡位置から不安定の変化
(3)まとめ
今回の記事のまとめを以下に示します。
(1)原点の渦に他の渦によって僅かな変位が与えられても,速度は「ゼロ」となるため,渦列の平衡位置は変化しない。
(2)渦列の時間経過によって,平衡状態から不安定になっていく。
以上です。最後まで閲覧頂きありがとうございました。
次回は,「カルマン渦列」について,解説する予定です。
※「三角関数の無限乗積」については,いつか記事にする予定です。
いいなと思ったら応援しよう!

