流体力学　渦に関する法則（その2）

　皆様おはこんばんちは。そして，お疲れ様です。

　最近，流体力学を再度学び直してみようと思い，記事にしています。
　第３４回目は，前回の予告通り「渦に関する法則」について紹介していきます。

（１）渦の何を取り扱うのか？

　 では，「渦に関する法則」について，解説していく訳ですが，筆者以外は，「何をそんなに取り上げる必要があるの？」と思うはずです。そこで，「渦に関する法則」として取り上げる内容を以下に箇条書きで示します。そして，各項目で記事にする予定ですので，興味のある分野や関連項目で見たいなどでいいかと思います。

（ⅰ）渦管を取巻く閉曲線Cで循環Γが成立するのか。
（ⅱ）2次元平面から3次元曲面でも循環Γが成立するのか。
（ⅲ）2次元流れの渦度は時間経過によってどう変化するのか。
（ⅳ）閉曲線Cに沿う循環Γは時間経過でどう変化するのか。

　基本的には，渦と取り扱うときに必ず登場する循環Γがどのようなモデルでも成立するのかをメインに取り扱います。今回は，「（ⅱ）2次元平面から3次元曲面でも循環Γが成立するのか。」について投稿していきます。

（２）2次元平面から3次元曲面でも循環Γが成立するのか。

（2-1）結論から

　今回は，結論から申します。2次元平面から3次元曲面でも循環Γは「成立します」。このことは，何となく皆さんも感覚的に成立するのは，わかるのではないでしょうか。
　では，モデル化によって渦管の断面で発生している渦運動の様子をどのようにして2次元から3次元にするのでしょうか。この答えは意外と簡単です。以前の記事で紹介したように，渦管の「1つの断面」を使って閉曲線Cと循環Γの関係を紐解くことをしてきましたが，これを「2つ以上の断面」に増やし，かつ「循環Γ，Γ'が同値である」ことを導けばよいのです。イメージとしては，図1に示すようなモデルです。図を見ると，渦管の断面を2つ以上見ていることが分かると思います。

図1　3次元曲面の循環Γのモデル

　図が示しているのは，渦が閉じて輪になり，無限遠方まで続くイメージです。そして，循環Γは一定値となることです。では，これを次項では，証明していきましょう。

（2-2）3次元曲面における循環Γの関係

　それでは，図2に示すように渦管の断面にそれぞれ循環Γ，Γ’が生じているモデルを考えます。また，これらの循環には経路a, b, c, d, e, f, g, hを設定しています。

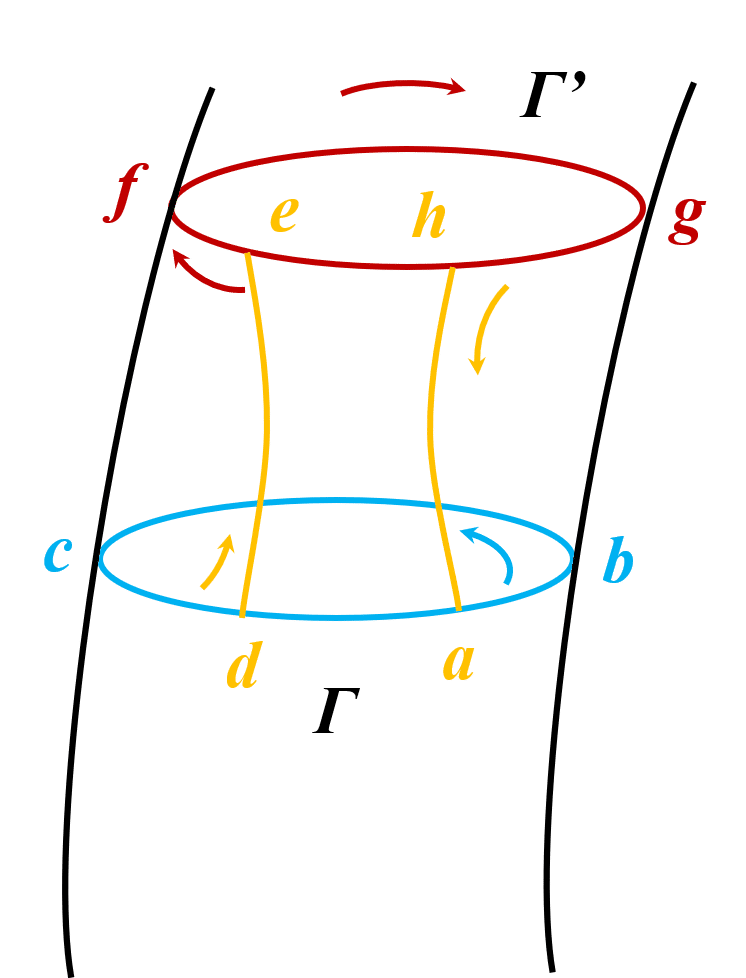
図2　循環Γ，Γ’の渦管断面モデルと断面経路

　まずは，渦管に生じた任意の横断面abcdの循環Γを考えると，式（１）のように表せます。

　次に，渦管に生じた他の任意の横断面hgfeの循環Γを考えると，式（2）のように表せます。

　ここで，今までに示しているモデル化した循環Γ，Γ‘の間隔はあえて広くしていますが，この2つの循環Γ，Γ’が無限に接近した状態を考えます（2直線ah，deに該当します）。このように，モデルに条件を加えることで，図3のように，2つの循環Γ，Γ’の間に渦面を貫くような渦（モデル上では閉曲線）が存在させなくさせることが出来ます。

図3　循環Γ，Γ’を繋ぐ2直線の関係

　これによって，全体の経路である閉曲線abcdefghの循環Γは，式（3）のように表せます。

　式（1），（2）を式（3）に代入すると，式（4）のように表せます。

　よって，2つの場所が異なる循環Γ，Γ‘は同値となることが分かりました。これにより，循環Γ，Γ’が2次元平面から3次元曲面でも成立することが分かってい頂けたのではないでしょうか。

（３）まとめ

　今回の記事のまとめを以下に示します。
（１）渦に関する法則は，主に4つ取り上げる。今回は，（ⅱ）2次元平面から3次元曲面でも循環Γが成立するのか。
（２）循環Γ，Γ‘は1つの渦管に他の横断面で同値で成立する。
（３）循環Γ，Γ‘を繋ぐ2直線の間隔を極限にまでに接近することで，2つの循環の間に渦（閉曲線）が発生することを防いでいる。

　以上です。最後まで閲覧頂きありがとうございました。

※次回は，「渦に関する法則（その3）」について扱う予定です。