
補足編 マクローリン展開
皆様おはこんばんちは。そして,お疲れ様です。
最近,流体力学を再度学び直してみようと思い,記事にしています。
今回は,第21回目に予定している「2重わき出し」で使用する予定の「マクローリン展開」について紹介していきます。最近,更新をサボっていた筆者のリハビリということで。
(1)マクローリン展開は「接線の方程式」と同じ?
さて,今後の記事で取り上げる予定の「マクローリン展開」についてですが,実は「接線の方程式」から始まるのです。よく高校・高専では,「微分=接戦を求めること」のように教えるようです。恐らく数学的に厳密な議論をすれば異なる部分があるのでしょうが,工学的に応用するには,この表現で十分なのです。そこで,微分の知識を交えたうえで接線の方程式を思い出してみましょう。図1には,接線の方程式の様子を図示したもの表し,y = f(x)のとき,式(1),(2)には「接線の方程式」をそれぞれ示します。

図1 接線の方程式
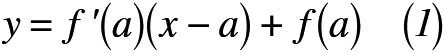
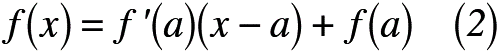
よって,式(2)は第1次近似できることを意味しています。イメージしづらいと思いますので,図2に第1次近似の実例を示します。

図2 第1次近似の実例
つまり,接線の方程式は言い換えると「近似公式」と取れることが分かって頂けたと思います。
(2)「第n次近似」すると,得られるのは?
ここで,前項の接線の方程式を使って,2次式でf(x)を近似しようと仮定したときは,式(3)のように表せます。
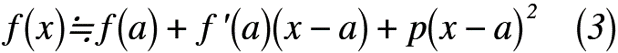
では,式(3)の両辺をxについて微分すると,式(4)のように表せます。

さらに,3次式でf(x)を近似しようと仮定したときは,式(5)のように表せます。

式(5)の両辺をxについて微分すると,式(6)のように表せます。

これより,右辺の次数を増加させていくと,近似精度が増加すると同時に式(7)のように表せます。また,式(7)は「テイラー展開」と言います。
![]()
式(7)は,y = f(a)の一般式で成立する近似式ですが,a=0の場合(つまり,任意の関数が原点を通過するときに相当)は,式(8)のように表せます。

式(8)を「マクローリン展開」と言います。以上のように,微分から接線の方程式,そしてテイラー展開,マクローリン展開と導けました。結論から言えば,「マクローリン展開」は,「関数を微分するとともに近似式を導出する」ためのツールなのです。
実は工学の世界では,この「マクローリン展開」を頻繁に使うことが多いので,数学的な厳密論までは触れなくても背景知識は知っておくと,なぜ「マクローリン展開」を使うのかが分かるのです。
(3)まとめ
今回の記事のまとめを以下に示します。
(1)接線の方程式は,「近似公式」とみなせる。
(2)微分の定義→接線の方程式→テイラー展開→マクローリン展開の順で導出できる。
(3)マクローリン展開は,関数が原点を通る場合に適用でき,工学の世界では「関数を微分するとともに近似式を導出する」ことと同義である。
以上です。最後まで閲覧頂きありがとうございました。
※本記事は,「2重わき出し」にて使用する背景知識です。もしかしたら,その他にも使うかもしれませんが…。
(4)おまけ
今回は,私の実体験を書いていきます。当時高専5年生の私は,必修であった「有限要素法」の講義でCAE (Computer Aided Engineering)で使用する要素について学んでいた時でした。
(※CAEは,コンピューター上で計算を行わせることで機械製品・土木建築物の構造解析,熱伝導解析,固有値解析及び流体解析など,実際の実験を行わなくてもおおよその予測ができる技術の総称です。)
講義中に扱ったのが,まさに「マクローリン展開」でした。そして,後の指導教員となる先生からは「マクローリン展開は,どこでも使うから必ず知っておくように」と言っていたものの,当時の私の感覚は「マクローリン展開なんて,今まで使った覚えがないのだが…」でした。
しかし,専攻科1年(大学3年と同じ時期)にゼミのために自主学習に励んでいたときに気づいたのです。
「めちゃマクローリン展開使うやん!」と…。
以下に,マクローリン展開を使ったときの一覧を示します(多分,抜けは大いにあるかと思いますが…)。
①マクローリン展開をそのまま適用するパターン
【材料力学・流体力学】
→微小要素での応力・圧力の算出
【材料力学・機械力学】
→カステリアーノの第2法則,エネルギー法による解法の証明
【機構学】
→往復スライダクランク機構(2次精度)
【伝熱工学】
→伝熱フィンの解析
②間接的にマクローリン展開を使うパターン
【工業熱力学】
→閉じた系・開いた形における熱力学第1法則の全微分,マックスウェルの関係式
③筆者が研究していたときに出会ったパターン
【内燃機関】
→定圧比熱の算出(3次精度,もしくは4次精度)
このような感じで,機械工学に限定してもこれだけ触れている回数が多いのです。恐ろしい…。知れば知るほど,知らなかったらどれだけよかったかと思うばかりです。汗
いいなと思ったら応援しよう!

