流体力学　翼理論（その4）

　皆様おはこんばんちは。
 
　最近，流体力学を再度学び直してみようと思い，記事にしています。
　第58回目は，「翼理論」について紹介したいと思います。今回は，その4としてジューコフスキーの仮説と循環の算出について取り上げたいと思います。

（1）ジューコフスキーの仮説

　今回は，前回の「翼理論（その3）」で円柱，平板翼等の周りの流れについて，数式に注目しました。そこでは，一様流れ，x軸に適当な傾き角αをなす一様流れとx軸に適当な傾き角αをなす一様流れに循環を加えたものを議論しました。なぜこのような流れで記事にしたのかを取り上げます。

「ロシアの航空の父」と評されている暇人ことニコライ・ジューコフスキーが提唱した仮説を紹介します。

「翼理論（その3）」でも取り上げた通り，z平面で半径aの円柱に速度u0の一様な流れがあたる場合は，ジューコフスキー変換でζ平面の長さ4aの平板に写像されることを示しました。この平板翼は，z平面のx軸に適当な傾き角αをなす一様流れの場合であっても同様です。そこで，適当な傾き角αをなす一様流れをx軸として考えると，図1のように考えることが出来ます。

図1　平板周りの流れ（左：一様流れ，中央：z平面のx軸に適当な傾き角αをなす一様流れ，右：x'軸に平行な一様流れ）

図1は，実際の一様な流れの中に平板がある傾きで置かれた状態と考えられます。ここで，平板の流れの変化を図2に示します。

図2　平板周りの流れの変化（左：x'軸に平行な一様流れ，中央：前端，後端に渦が発生，右：後端の渦が後方に流れる）

　図2のような流れの中に平板がある傾きで置かれると，平板の周りの流れに注目すると，はじめのうちは対称的な循環のない流れができます。

　次に，流体の持つ粘性作用により，平板の両端にそれぞれ渦の領域が発生します。

　その後，前端の平板には渦が残るのに対し，後端の平板には渦がさらに後方に流されることを突き止めました。そこで，ジューコフスキーは翼（図2では，平板）の後端が後方の岐点となり，流れは板に沿って滑らかに流れ去ると仮定しました。具体的には，翼（平板）に「循環」が生じると仮定したのです。これを「ジューコフスキーの仮説」といい，現在はこの仮説は正しいとされており，循環とベルヌーイの定理の2つで，翼（平板）周りの流れは説明ができるのです。

よって，「翼理論（その3）」で説明した内容は「ジューコフスキーの仮説」を解説したに過ぎないということです。しかし，前回の「翼理論（その3）」では，肝心の循環に焦点を当てていないので，次項では「循環」に注目しましょう。
 

（2）z平面のx軸に適当な傾き角αをなす一様流れと循環を加えた場合の循環

　次に取り上げるのは，z軸と適当な傾き角αをなす一様流れと循環を加えた場合の循環を求めてみましょう。

　前回の「翼理論（その3）」でｚ平面の半径aの円は，ζ平面の長さ4aの平板になり，図3のようになることも確認しました。図3からも分かるように板の後端はζ=2aは，z平面における円柱ではz=aに対応します。

図3　x軸に適当な傾き角αをなす一様流れのz平面とジューコフスキー変換後のζ平面

ここで，ジューコフスキーの仮説に従って平板の後端にそって流れ去る状態，言い換えるとz平面でz=aが淀み点になるために数式を考えると，式（1）のようになります。式（1）は，「翼理論（その3）」でも解説していますが，複素ポテンシャルwから複素速度dw/dzを求めるために複素数zについて微分した結果，淀み点（速度が「ゼロ」になる点）を利用することで複素速度dw/dzが「ゼロ」になることを利用した2次方程式です。

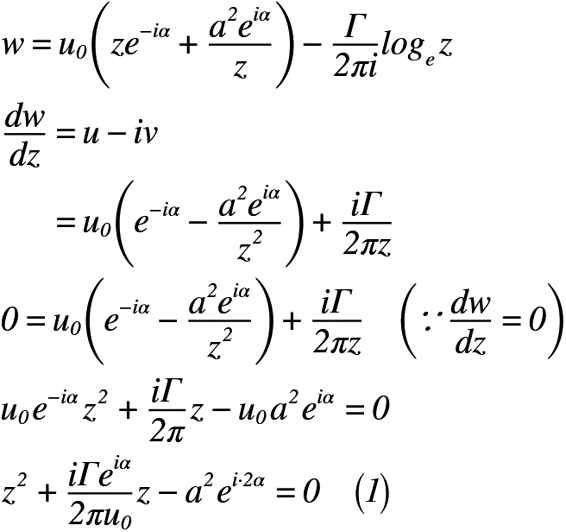
　ここで，とz平面でz=aが淀み点になるために式（1）をz=aに変換すると，式（2）のようになり，z平面のx軸に適当な傾き角αをなす一様流れの循環を求めることが出来ます。

　式（2）を眺めると，影響する因子は平板の長さa，流体の速度u0，z平面のx軸に適当な傾き角αの3つであり，いずれも比例関係（例；速度大→循環大）で成立するということになります。
 これで，ジューコフスキーの仮説に従った循環を求めることが出来ました。次項では，ζ平面における円弧翼の循環を算出していきます。

（3）円弧翼の循環

　今度は，図4に示すような円弧翼の循環を求めてみましょう。

図3　z平面における原点からy軸方向に移動した半径a0の円かつx軸に適当な傾き角αをなす
一様流れとζ平面における円弧翼

図4に示すようなz平面における半径a0の円をζ平面における円弧翼へ変換するためのジューコフスキー変換は，式（3）のように表されます。

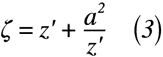
ここで，x’軸を流れの方向になるように座標x’，y’をとり，z’=x’+iy’としてz’座標において，x’軸に平行な速度u0の一様な流れの中に強さ－Γの循環を持つ円の周りの複素ポテンシャルwは，式（4）のように表されます。

図4から複素数zは，z=z’e^iα+ifとなるので，複素数z’は式（5）のようになり，式（4）に式（5）を代入すると，式（6）となります。

また，図4においてz=aが淀み点となるため，式（6）を複素数zについて微分した複素速度dw/dzが「ゼロ」として計算ができるようになります。追加で，図4からif-a=a0e^i(π-β)となる関係も利用すると，式（7）のように表されます。

式（7）で得られた2次方程式から循環Γを求めると，式（8）のようになります。

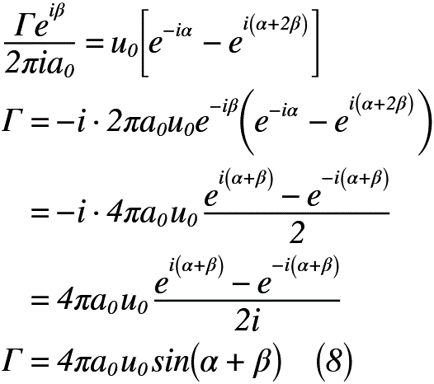
式（8）は，三角関数の相互関係と幾何学的性質を利用すると，式（9）のように書き換えることもできます。

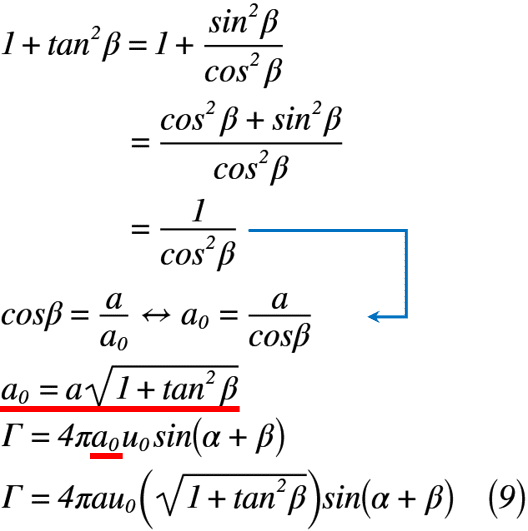
　以上の結果から円弧翼の循環は，平板の長さa，流体の速度u0，z平面のx軸に適当な傾き角α以外に，z平面のy軸に適当な傾き角βも影響する因子となります。
 

（4）まとめ

 今回の記事のまとめを以下に示します。
①     ジューコフスキーの仮説は，平板に流れる流れの様子から後端の渦が後方に流れることを「循環」を使って説明した内容である。
②     z平面のx軸に適当な傾き角αをなす一様流れと循環を加えた場合の循環は，平板の長さa，流体の速度u0，z平面のx軸に適当な傾き角αの3つのみが影響する因子である。
③     円弧翼の循環は， 平板の長さa，流体の速度u0，z平面のx軸に適当な傾き角α以外に，z平面のy軸に適当な傾き角βも影響する因子となる。

以上です。最後まで閲覧頂きありがとうございました。
次回は，「ブラジウスの第1公式」について，解説する予定です。