数学コラム第5回　6角形問題（開成中）の振り返り

みなさま、まっちゃんスターです。

さ、数学コラムも第5回目になりました。

だんだん、自分の中の投稿るーるとかも少しずつ見えてきている段階かもですね。まだ模索中ですが笑

なんにせよ、開成中の問題ですが、6角形の比ですかね。

六角形というよりは、俺ルールでまとめる

正三角形の中点　全体の1/４

正方形　全体の１/２

六角形　全体の３/４※今回の問題

とまあ、続くのですが、ざっとまっちゃんまとめですと

全体の大きさSとした場合、中点のｎ角形における面積の大きさは

S・（sin（n-2)π/２ｎ）＾２

という性質をもっている。

これは、黒い部分の角辺を半径ｒとして、赤い部分は

ｒ・sin（n-2)π/２ｎ

になっている性質をもっている。

面積は、その2乗の影響をもっているので、

今回はこれを適合した。

正六角形であれば、角度120°より、その半角60°は

sin60°＝√３/２

この2乗は3/４なので、ものは成立している。

さらに、半分ではなく回転するものと考える

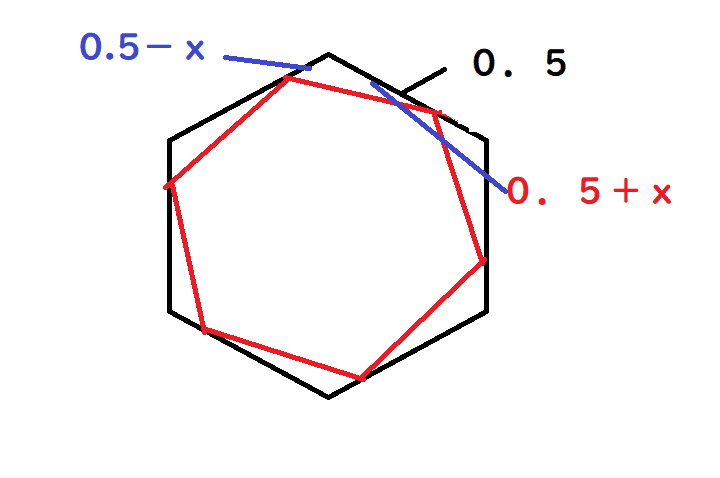
こんな感じですかね？

そうしますと

0.5＋２ｘ＾２－２（0.25－ｘ＾２）cos（n-2)π/ｎ

なので、

0.5（１ーcos（n-2)π/ｎ）＋２ｘ＾２（１＋cos（n-2)π/ｎ）

※正方形は丁度cos９０からコサインが消える形となる。

ともかける

ただ、これはもうちょっと高度な表現で、まじで補足レベルな話なので、

頭が痛くなるくらいならこれはみなかったことにしていただければと思う。

開成中のを解説してたら、この法則みつけたもので笑笑

なんにせよ、今回のコラムも終わります

また次回もお楽しみに

またね😏