高校数学１０分プログラミング（数学B編 2.空間のベクトル）8日目「球面の方程式を考える」解説

マガジンリスト　＞　数学B編 2.空間のベクトル　＞　8日目 解説

本日の課題、おつかれさまでした。

課題の球面の方程式を用いて球面を描くプログラムを作成することができたでしょうか。

解答例

今回の課題の球面の方程式を用いて球面を描くプログラムの例を示します。

// 球面を描く

float range; // 座標系での表示範囲-range≦x,y.z≦range
float res; // 座標系のサイズをキャンバスのサイズに変換するパラメータ
float angle = 0.0;

PVector c1,c2,c3,c4; // 問題の球面の中心位置を表わすベクトル
float r1,r2,r3,r4;// 問題の球面の半径
PVector a3; // 問題(3)の点Aを表わすベクトル
PVector a4, b4; // 問題(4)の点A,Bを表わすベクトル

void setup(){
  size(400, 400, P3D);
  noFill();
  ortho();
  range = 10.0; 
  res = width / 2.0 / range;

  // (1)中心が原点、半径が2の球面
  c1 = new PVector(0.0,0.0,0.0);
  r1 = 2.0;

  // (2)中心がC(1,2,3)、半径が3の球面
  c2 = new PVector(1.0,2.0,3.0);
  r2 = 3.0;

  // (3)中心がC(1,3,-1)で、点A(5,-1,1)を通る球面
  a3 = new PVector(5.0,-1.0,1.0);
  c3 = new PVector(1.0,3.0,-1.0);
  r3 = a3.copy().sub( c3.copy() ).mag();

  // (4)2点A(-1,2,3)、B(3,6,-1)を直径の両端とする球面
  a4 = new PVector(-1.0,2.0,3.0);
  b4 = new PVector(3.0,6.0,-1.0);
  c4 = a4.copy().add( b4.copy() ).mult(0.5);
  r4 = a4.copy().sub( b4.copy() ).mag()/2.0;
  
  println("r3=", r3);
  println("c4=", c4);
  println("r4=", r4);
  
}

void draw(){
  background(204); // 背景をグレーにする
  // 視点を設定する
  camera(200.0, -200.0, 100.0, 0.0, 0.0, 0.0, 0.0, 0.0, -1.0);
  // マウスボタンが押されたときの処理
  if(mousePressed){ 
    if( mouseButton == LEFT ){ // 左ボタンがおされたときはz軸時計周りに回転
      angle = angle + 1.0;
    } else if( mouseButton == RIGHT ){ // 右ボタンがおされたときはz軸反時計周りに回転
      angle = angle -1.0;
    } else {
    }
  }
  // z軸周りに回転
  rotateZ(radians(angle));

  // 座標軸の設定
  fill(255,0,0);
  stroke(255,0,0);
  arrow3D(0.0,0.0,0.0,range * res,0.0,0.0); // x軸（赤色）
  fill(0,255,0);
  stroke(0,255,0);
  arrow3D(0.0,0.0,0.0,0.0,range * res,0.0); // y軸（緑色）
  fill(0,0,255);
  stroke(0,0,255);
  arrow3D(0.0,0.0,0.0,0.0,0.0,range * res); // z軸（青色）

  noFill();
  stroke(0,0,0);
  // 以下に、図形を描いていく

  // (1)中心が原点、半径が2の球面 (黄色）
  strokeWeight(5);
  stroke(255,255,0);
  point_rhs(c1.copy().mult(res));
  strokeWeight(1);
  stroke(255,255,0,20);
  noFill();
  sphere_rhs(c1.copy().mult(res), r1*res);
  
  // (2)中心がC(1,2,3)、半径が3の球面（水色）
  strokeWeight(5);
  stroke(0,255,255);
  point_rhs(c2.copy().mult(res));
  strokeWeight(1);
  stroke(0,255,255,20);
  noFill();
  sphere_rhs(c2.copy().mult(res), r2*res);
  
  // (3)中心がC(1,3,-1)で、点A(5,-1,1)を通る球面（桃色）
  strokeWeight(5);
  stroke(255,0,255);
  point_rhs(c3.copy().mult(res));
  point_rhs(a3.copy().mult(res));
  strokeWeight(1);
  stroke(255,0,255,20);
  noFill();
  sphere_rhs(c3.copy().mult(res), r3*res);
  
  // (4)2点A(-1,2,3)、B(3,6,-1)を直径の両端とする球面（白色）
  strokeWeight(5);
  stroke(255,255,255);
  point_rhs(a4.copy().mult(res));
  point_rhs(b4.copy().mult(res));
  strokeWeight(1);
  stroke(255,255,255,50);
  noFill();
  sphere_rhs(c4.copy().mult(res), r4*res);

}

ソースコード2　球面の方程式を用いて球面を描くプログラム（完成版）

ソースコード2を、スケッチ「drawSpheres」のテキストエディタ部分に書いて実行すると、図1のように、実行ウィンドウのキャンバスに空間の座標系を表す３つの空間ベクトル（赤色：$${x}$$軸、緑色：$${y}$$軸、青色：$${z}$$軸）を基準にして、
(1) 中心が原点、半径が$${2}$$の球面を黄色、
(2) 中心が$${\mathrm{C}(1,2,3)}$$、半径が$${3}$$の球面を水色、
(3) 中心が$${\mathrm{C}(1,3,-1)}$$で、点$${\mathrm{A}(5,-1,1)}$$を通る球面を桃色、
(4) 2点$${\mathrm{A}(-1,2,3),\mathrm{B}(3,6,-1)}$$を直径の両端とする球面を白色
で表示します。

図1　球面の描画

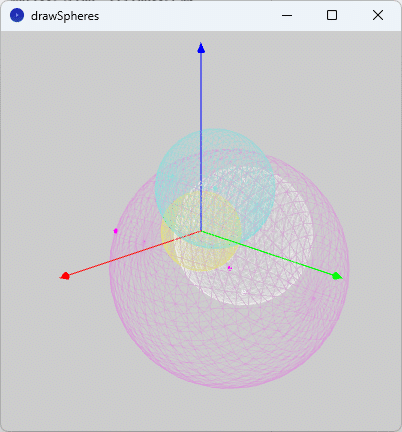
なお、実行ウィンドウのキャンバス内をクリックすると$${z}$$軸回りに図形が回転するので、いろいろな角度から図形を眺めてみてください。

また、参考までに課題(3)の球面の半径 r3 、課題(4)の球面の中心 c4 と半径 r4 がコンソールに出力しています（図2）。

r3= 6.0
c4= [ 1.0, 4.0, 1.0 ]
r4= 3.4641016

図2　スケッチ「drawSpheres」の実行結果

球面の方程式の導出

各課題の球面の方程式を求めると、以下のようになります。
(1)の球面の方程式は、

$$
x^2+y^2+z^2=2^2
$$

です。(2)の球面の方程式は、

$$
(x-1)^2+(y-2)^2+(z-3)^2=3^2
$$

となります。(3)の球面の方程式は点$${\mathrm{A}}$$を通るので、球面の半径$${r_3}$$は

$$
r_3 = \mathrm{ACの長さ} = 6
$$

となり、

$$
(x-1)^2+(y-3)^2+(z+1)^2=6^2
$$

となります。最後に、(4)の球面の方程式は、点$${\mathrm{A,B}}$$を直径の両端とするので、中心は線分$${\mathrm{AB}}$$の中点$${(1,4,1)}$$となり、半径は線分$${\mathrm{AB}}$$の長さの半分の$${2\sqrt{3}}$$となり、方程式は、

$$
(x-1)^2+(y-4)^2+(z-1)^2=12
$$

となります。
これらの方程式と実際に描いた球面の図形、コンソールに出力された値を比較してみておいてください。

本日は以上です。
明日は、平面の方程式について考えていきます。

明日もよろしくお願いします。

読んだ感想などをお寄せください

本記事を読んだ感想や質問などを以下のお問い合せフォームからお寄せください。（お問合せフォームの本文に、本記事のタイトルを入れてください。）

お問い合わせ | note（ノート）

MK’s papa