高校数学１０分プログラミング（数学Ⅱ編 3.三角関数）15日目「三角関数の合成を考える」解説

マガジンリスト　＞　数学Ⅱ編 3.三角関数　＞　15日目 解説

本日の課題、おつかれさまでした。

課題の三角関数の合成を行ってそのグラフを描くプログラムを作成することができたでしょうか。

解答例

今回の課題の三角関数の合成を行ってそのグラフを描くプログラムの例を示します。

float x_range = 10.0; // x軸の表示範囲 -x_rangeからx_rangeまで
float y_range = 10.0; // y軸の表示範囲 -y_rangeからy_rangeまで 

void setup(){
  size(500,500);
  noLoop();

  setAxes(x_range, y_range); // 座標軸の準備
  
  noFill();

  float a = 1.0;         // sin関数の係数
  float b = -sqrt(3.0);  // cos関数の係数

  // (1) y = a sinθ
  stroke(255,0,0);
  float A = a; // 振幅
  float k = 1.0; // θの係数
  float alpha = 0.0; // 位相
  float y1 = 0.0; // y軸方向の移動量
  draw_sin(A,k,alpha,y1);
    
  // (2) y =  b cosθ
  stroke(0,0,255);
  A = b; // 振幅
  k = 1.0; // θの係数
  alpha = 0.0; // 位相
  y1 = 0.0; // y軸方向の移動量
  draw_cos(A,k,alpha,y1);    

  // (3) 合成関数
  stroke(0,0,0);
  A = sqrt(a*a+b*b); // 振幅
  k = 1.0; // θの係数
  alpha = atan2(b, a); // 位相
  y1 = 0.0; // y軸方向の移動量
  draw_sin(A,k,-alpha,y1); 

}

// sinカーブ y=A sin(k(θ-alpha))+y1 を描く関数
void draw_sin(
  float A, // 振幅
  float k, // θの係数
  float alpha, // 位相
  float y1 // y軸方向の移動量
){
  // グラフの定義域
  float x_min = -x_range;
  float x_max = x_range;
  int plot_num = 200; // グラフを描くための頂点の個数  
  
  // グラフを描画
  float x, y; // 関数の座標
  float X, Y; // キャンバス上の座標 
  beginShape();
  for(int i=0; i<=plot_num; i++){
    x = x_min + (x_max - x_min) / plot_num * i; // sinカーブ上の点のx座標
    y = A * sin( k*(x-alpha) ) + y1; // sinカーブ上の点のyの値
    // キャンバス上の座標位置に換算
    X = width / 2.0 / x_range * x;
    Y = height / 2.0 / y_range * y;
    vertex(X, Y);
  }
  endShape();

}

// cosカーブ y=A cos(k(θ-alpha))+y1 を描く関数
void draw_cos(
  float A, // 振幅
  float k, // θの係数
  float alpha, // 位相
  float y1 // y軸方向の移動量
){
  // グラフの定義域
  float x_min = -x_range;
  float x_max = x_range;
  int plot_num = 200; // グラフを描くための頂点の個数  
  
  // グラフを描画
  float x, y; // 関数の座標
  float X, Y; // キャンバス上の座標 
  beginShape();
  for(int i=0; i<=plot_num; i++){
    x = x_min + (x_max - x_min) / plot_num * i; // cosカーブ上の点のx座標
    y = A * cos( k*(x-alpha) ) + y1; // cosカーブ上の点のyの値
    // キャンバス上の座標位置に換算
    X = width / 2.0 / x_range * x;
    Y = height / 2.0 / y_range * y;
    vertex(X, Y);
  }
  endShape();

}

ソースコード2　三角関数の合成を行ってそのグラフを描くプログラム

スケッチ「check_sum2prod_formula」の「check_sum2prod_formula」タブのテキストエディタ部分をソースコード2で書き換えて実行すると、実行ウィンドウのキャンバス上に、課題(1)のグラフが赤色、課題(2)のグラフが青色、課題(3)のグラフが黒色でそれぞれ描かれます（図2）。

図2　合成前後の三角関数のグラフ

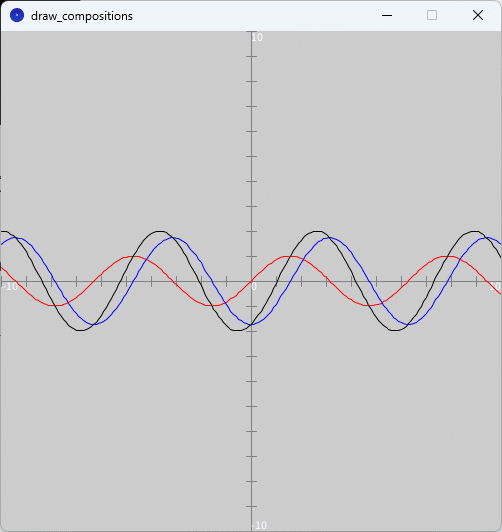
このグラフをみると、赤色（課題(1)）の三角関数のグラフと青色（課題(2)）の三角関数のグラフを足し合わせたものが、ちょうど合成した三角関数（課題(3)）のグラフになっていることがわかります。

本日は以上です。
次回からは、指数関数と対数関数に関する問題を考えていきます。

次回からもよろしくお願いします。

※今回の課題とその解答例について質問や疑問がある方は、本記事の下部にあるコメント欄からお願いします。

MK’s papa