状態空間モデルを使って株価を予測する

状態空間モデルとは

 状態空間モデルの歴史は古く、1950年代から1960年代にかけて、航空機、ミサイルといった動的システムの挙動をモデル化し、リアルタイムで制御したいというニーズから発達しました。

これらのシステムの挙動は高度に動的であり、刻々と変化する情報（状態）を基に制御を行う必要があります。しかし、システムの内部状態は直接観測できないため、外部からの観測データ（レーダー測定値など）を基に、内部の「状態」を推定し、それを使ってシステムを制御する技術が必要とされました。

この問題に対処するために1960年にルドルフ・E・カルマンが考案したのが、カルマンフィルター（Kalman Filter）です。これは線形ガウスシステムの状態の最適推定を行う手法であり、特にノイズを含むデータに対してもロバストな推定ができるなど革新的なアイデアが提案されました。

1960年代から1970年代にかけて、状態空間モデルは科学技術領域のみならず経済学や統計学の分野へも展開していきます。経済や金融市場のデータは時間とともに変化し、その変動には観測できない要因（潜在的なトレンドや季節性など）が大きな役割を果たす点で、状態空間モデルとの親和性が高いのです。

例えば、トレンドや季節変動が含まれる非定常データを明示的に扱うために、SARIMAやGARCHなど複雑な時系列モデルが考案されています。これらのモデルは状態空間モデルとしてとらえることにより、観測されない潜在変数をモデルに組み込み、カルマンフィルターを始めとした制御技術の分野で高度に発達した技法を活用することができるメリットがあります。

この記事では状態空間モデルの一般的な構成を紹介し、適用例として株価の予測を行うサンプルコードを共有します。数式の記法は統計分析ソフトウェアstatsmodelsの状態空間モデルのドキュメントも参考していますので、statsmodelsの説明ドキュメントや例題も参照すると理解が進みやすいと思います。

1. 状態空間モデルの構成

状態空間モデルは、次の2つの主要な方程式で構成されます。

• 状態方程式 (State equation)
  システムの内部状態が時間的にどのように推移するか（遷移）を定義する。

• 観測方程式 (Observation equation)
  外部から観測可能なデータ（観測データ）と、内部状態との関係を定義する。

【状態方程式 (State Equation) 】

状態方程式は、内部状態 $${x_t}$$ の時間的推移方法を記述します。

$$
\alpha_{t+1} = T_t \alpha_t + c_t + R_t \eta_t, \quad \eta_t \sim \mathcal{N}(0, Q_t)
$$

ここで、

$${ \alpha_t }$$: 時刻 $${t}$$ における$${k_{states} \times 1}$$ の状態列ベクトル。
$${ T_t }$$: $${k_{states} \times k_{states}}$$ の遷移行列。状態の時間的な推移を表す。
$${ c_t }$$: $${k_{states} \times 1}$$ の状態切片。時刻 $${t}$$ におけるレベル（オフセット）。
$${ R_t }$$: $${k_{states} \times k_{posdef}}$$ の選択行列。摂動（外部擾乱）が状態ベクトルに与える影響を示す。
$${ \eta_t }$$: $${k_{posdef} \times 1}$$ の摂動ベクトル。各要素はホワイトノイズであり、 $${k_{posdef} \times k_{posdef}}$$ の共分散行列 $${Q_t}$$ を持つ。

【観測方程式 (Observation Equation) 】

観測方程式は、観測データ $${y_t}$$ が状態 $${\alpha_t}$$ に基づいて生成される変換式を表します。

$$
y_t = Z_t \alpha_t + d_t + \epsilon_t, \quad \epsilon_t \sim \mathcal{N}(0, H_t)
$$

ここで、

$${ y_t }$$: $${k_{endog} \times 1}$$ の観測データベクトル（時刻 $${t}$$ における観測値）。
$${ Z_t }$$: $${k_{endog} \times k_{states}}$$ の設計行列（観測データと状態の関係を表す）。状態が直接観測される場合は単位行列。
$${ \alpha_t }$$: $${k_{states} \times 1}$$ の状態ベクトル（時刻 $${t}$$ における内部状態）。
$${ d_t }$$: $${k_{endog} \times 1}$$ の観測切片（時刻 $${t}$$ におけるオフセット）。
$${ \epsilon_t }$$: $${k_{endog} \times 1}$$ の観測誤差ベクトル。各要素はホワイトノイズであり、$${k_{endog} \times k_{endog}}$$ の共分散行列 $${H_t}$$ を持つ。

このようにして、状態空間モデルは観測データと内部状態の動的な関係を数学的にモデル化し、観測誤差と状態摂動の両方を考慮しながら、時間的推移を予測することができます。

以下に、ポピュラーな時系列モデルが、状態空間モデルを使うことでどのように表現されるのか見ていきます。

ARモデルの状態空間表現

自己回帰時系列モデル AR(p)を次のように定義します。

$$
y_t = \phi_1 y_{t-1} + \phi_2 y_{t-2} + \dots + \phi_p y_{t-p} + \epsilon_t
$$

ここで、

$${y_t}$$: 時刻 $${t}$$ における観測値。
$${\phi_1, \phi_2, \dots, \phi_p}$$: 自己回帰係数。
$${\epsilon_t \sim \mathcal{N}(0, \sigma^2)}$$　すなわち、$${\epsilon_t}$$: 平均0、分散 $${\sigma^2}$$ の白色雑音（ホワイトノイズ）。

AR(p) の状態空間モデル化では、状態ベクトル $${\alpha_t}$$ は過去の観測値から構成される $${p}$$ 次元のベクトルとして定義します。そして状態方程式と観測方程式を通じて観測値 $${y_t}$$ を予測・更新します。

$$
\alpha_t =
\begin{pmatrix}
y_t \\
y_{t-1} \\
\vdots \\
y_{t-(p-1)} \\
\end{pmatrix}
$$

状態方程式は、状態ベクトル $${\alpha_t}$$ の時間遷移を示します。状態方程式の定数項はこの場合無いので、以下のように表すことができます。

$$
\alpha_{t+1} = T \alpha_t +R \eta_t
$$

遷移行列 $${T}$$ は次のように定義します。

$$
T =
\begin{pmatrix}
\phi_1 & \phi_2 & \dots & \phi_p  \\
1 & 0 & \dots & 0  \\
0 & 1 & \dots & 0  \\
\vdots & \vdots & \ddots & \vdots  \\
0 & 0 & \dots & 1 \\
\end{pmatrix}
$$

選択行列 $${R_t}$$ は定数のベクトル R として表現できます。

$$
R = \begin{pmatrix}
1 \\
0 \\
\vdots \\
0 \\
\end{pmatrix}
$$

状態ベクトル $${\alpha_t}$$ の最初の成分がそのまま観測値になるとみなすので、誤差項 $${\epsilon_t}$$ は無しとします。従って観測方程式は以下のように定義します。

$$
y_t = Z \alpha_t
$$

ここで、設計行列 $${Z = \begin{pmatrix} 1 & 0 & \dots & 0 \end{pmatrix}}$$ 。

$${\eta_t}$$は、$${\epsilon_t}$$と同一です。 すなわち、$${\eta_t \equiv \epsilon_t \sim \mathcal{N}(0, \sigma^2)}$$

MAモデルの状態空間表現

移動平均時系列モデル MA($${q}$$)を次のように定義します。

$$
y_t = \epsilon_t + \theta_1 \epsilon_{t-1} + \theta_2 \epsilon_{t-2} + \dots + \theta_q \epsilon_{t-q}, \quad \epsilon_t \sim \mathcal{N}(0, \sigma^2)
$$

状態ベクトル $${\alpha_t}$$ は、過去の誤差項 $${\epsilon_{t-1}, \epsilon_{t-2}, \dots, \epsilon_{t-q}}$$ から構成される $${q}$$ 次元の列ベクトルとして定義します。

$$
\alpha_t =
\begin{pmatrix}
\epsilon_{t-1} \\
\epsilon_{t-2} \\
\vdots \\
\epsilon_{t-q} \\
\end{pmatrix}
$$

観測方程式は、観測データ $${y_t}$$ は状態ベクトル $${\alpha_t}$$ の線形結合として表されます。定数項はありません。

$$
y_t = Z \alpha_t
$$

設計行列は、$${Z = \begin{pmatrix} 1 & \theta_1 & \theta_2 & \dots & \theta_q \end{pmatrix}}$$ 。

状態方程式は、

$$
\alpha_{t+1} = T \alpha_t + R \eta_t
$$

$${q}$$ x $${q}$$ 遷移行列 $${T}$$ 、選択行列 $${R}$$ はそれぞれ以下のように定義します。遷移行列は状態ベクトルの要素を時間シフトする作用を定義した行列になっています。

$$
T =
\begin{pmatrix}
0 & 0 & \dots & 0 & 0 \\
1 & 0 & \dots & 0 & 0 \\
0 & 1 & \dots & 0 & 0 \\
\vdots & \vdots & \ddots & \vdots & \vdots \\
0 & 0 & \dots & 1 & 0 \\
0 & 0 & \dots & 0 & 0 \\
\end{pmatrix}
$$

$$
R = \begin{pmatrix}
1 \\
0 \\
\vdots \\
0 \\
\end{pmatrix}
$$

$${\eta_t}$$は、$${\epsilon_t}$$と同一です。 $${\eta_t \equiv \epsilon_t \sim \mathcal{N}(0, \sigma^2)}$$

上述の他にもARIMA、SARIMA、ARCH、GARCHなど様々なモデルに対して状態空間を使った定式化が可能です。ただし式がかなり煩雑になってきますのでここでは同様の説明は省略します。

2. 予測を実践する

この項では状態空間モデルを実際の金融・経済系データに適用した場合、どのような予測ができるのかを、サンプルコードを動かして見ていこうと思います。テーマは「トヨタ自動車の株価を米国・日本の主要金融・経済指標から予測する」です。なお以下の予測コードでは、企業業績や企業のファンダメンタル情報は直接の入力情報として使わないことを注記しておきます。

さて、ドル建て日経平均株価は、ＮＹダウ株価指数に対して従属的に動く、という説があります（Financial Trend、2010年、第一生命発行）。現在でもこの説が通用するならば、日経平均株価を構成する主要銘柄であるトヨタ自動車の株価の値動きは、日経平均株価及びに米国の主要金融・経済指標からなんらか影響を受けると考えてよさそうです。ただし筆者は適切な指標選択に対する見識を有していませんのでここではアプリオリに以下を環境変数（外生変数）として設定することにします。

- 日経平均株価
- ドル円為替レート
- 米国国債長短金利スプレッド（10年物金利と2年物金利の差）
- 失業率（Unemployment Rate）
- 個人消費支出（Personal Consumption Expenditures,PCE）

statsmodelでは表現力の高い状態空間モデルとして未観測成分モデル（Unobserved Components Model,UCM ）あるいはSARIMAXを利用することができます。これらは関数の呼び出しコード１行の相違以外コードを共通化できるので便利です。

以下に二種類のモデル化方法を簡単にまとめておきます。

未観測成分モデル（UCM）

以下は外生変数を考慮したUCMの観測方程式です。

$$
y_t = Z_t \alpha_t + g_t X_t + \epsilon_t
$$

$${ X_t }$$は、時点 $${ t }$$ における外生変数のベクトルであり、$${ g_t }$$ は外生変数に対する係数ベクトルです。

未観測成分モデルは、時系列データを観測できない成分の和として表します。

$$
y_t = \mu_t + \gamma_t + c_t +  \epsilon_t
$$

各成分は

$${ y_t }$$ : 観測された時系列データ  
$${ \mu_t }$$ : トレンド成分。ランダムウォーク、ローカル線形トレンドなど、さまざまな形でモデル化できます。  
$${ \gamma_t }$$ : 季節成分。周期的に繰り返されるパターンであり、四半期や月などの頻度に応じて変動します。  
$${ c_t }$$ : 循環成分。特定の周波数で振動する成分を表します。一般的には、減衰係数と周期を用いて定義します。  
$${ \epsilon_t }$$ : 誤差項（ホワイトノイズ）  

状態空間モデルの一般定義式に照らし合わせると、状態変数 $${\alpha_t}$$ は、上記のトレンド成分、季節成分、そして循環成分から構成されます。具体的な構成は着目する成分により異なってきます。ここでは割愛しますが詳細は statsmodels のドキュメント を参照ください。

SARIMAX（Seasonal ARIMA with eXogeneous regressors）

`statsmodels` の `SARIMAX` モデルは、状態空間モデルとして自己回帰（AR）、移動平均（MA）、季節性（S）、外生変数（X）を組み合わせたモデル SARIMAX($${ p, d, q \times P, D, Q, s }$$) を提供します。このモデルは、次のような一般的な構造を持っています。

$$
\Phi(L^s) \phi(L) (1 - L)^d (1 - L^s)^D y_t = \Theta(L^s) \theta(L) \epsilon_t + X_t \beta
$$

ここで、

$${ y_t }$$ は観測値。  
$${ \epsilon_t }$$ はホワイトノイズ。  
$${ \phi(L) }$$ と $${ \theta(L) }$$ は、通常の自己回帰および移動平均の多項式。  
$${ \Phi(L^s) }$$ と $${ \Theta(L^s) }$$ は、季節性自己回帰および移動平均の多項式。  
$${ L }$$ はバックシフト演算子（$${ L y_t = y_{t-1} }$$）。  
$${ d }$$ と $${ D }$$ はそれぞれ非季節性および季節性の差分次数。  
$${ s }$$ は季節の周期。  
$${ X_t }$$ は外生変数の行列で、$${ \beta }$$ はその係数ベクトル。  

以下にサンプルコードを記載します。

• データはインターネットからダウンロードできるものから選定しています。日次の株価、為替データはyahoo_finで取得、その他はpandas_datareaderを使っています。後者はデータソースとして米国連銀（FRED）のサイト を利用しています。このサイトはアカウント登録不要で、網羅的かつ使い勝手がよいのでお勧めです。

• 値の範囲が大きく異なるデータが混在する場合、学習に失敗しないようスケーリングを掛けることが常道ですが、このコードでは、変化率（株価でいえば収益率）に変換して関係性を調べています。

• テストデータは予測ウィンドウ期間（１か月）を定義して、各月ごとに１か月分の株価を予測します。外生変数有りの予測（赤いラインチャート）と、外生変数無しの予測（ピンクのラインチャート）を作成しています。

• 観測方程式の定義では時刻 T での観測データは同じ時刻 T での外生変数から影響を受けます。しかし株価に適用した場合、日付 T でのトヨタの株価が影響を受けるのは日付 T-1 以前の外生変数になりますので、全ての外生変数を一日分シフトしています。

# tsa_statespace_predi_return.py
# 状態空間モデルにより株価収益率を予測する
# Unobserved Components Model と SARIMAXを比較する
import pandas as pd
import numpy as np
from yahoo_fin import stock_info
import pandas_datareader.data as web
import statsmodels.api as sm
from statsmodels.tsa.statespace.sarimax import SARIMAX
import matplotlib.pyplot as plt
import japanize_matplotlib
import datetime
import matplotlib.dates as mdates
import warnings
from statsmodels.tools.sm_exceptions import ConvergenceWarning
# 特定の警告を無視
warnings.filterwarnings("ignore", category=FutureWarning)
warnings.filterwarnings("ignore", category=UserWarning)  # ValueWarningはUserWarningに含まれます
warnings.filterwarnings("ignore", category=ConvergenceWarning)

def interporate_df(daily_df):
    # 現在のデータの最新日付を取得
    latest_date = daily_df.index[-1]
    # 最新の日付の月の月末を取得
    month_end = latest_date + pd.offsets.MonthEnd(0)
    # 同じ月の月末までデータを補完
    if latest_date < month_end:
        extended_index = pd.date_range(start=latest_date + pd.Timedelta(days=1), end=month_end, freq='D')
        last_value = daily_df.iloc[-1,0:1].values.flatten()[0]
        extended_df = pd.DataFrame(last_value, index=extended_index,columns=daily_df.columns)
        daily_df = pd.concat([daily_df, extended_df])

    return daily_df

# 1. 期間を設定
start_date = '2020-01-01'
train_end = '2024-10-31'
test_start = '2024-02-01'
test_end = '2024-10-31'
end_date = '2024-12-31'

# 2. 株価データ（yahoo finnance usがソース）
symbols = ['7203.T','AAPL', 'MSFT', 'GOOG', 'AMZN', 'TSLA']
stock_price = stock_info.get_data(symbols[0], start_date=start_date, end_date=end_date)['close']
stock_returns = stock_price.pct_change().dropna()

# 3. 各ファクターのデータ取得（ドル円為替レート、失業率、個人消費、金利スプレッド、日経平均株価）
usd_jpy = stock_info.get_data("JPY=X", start_date=start_date, end_date=end_date)['close'].pct_change()
unrate = web.DataReader('UNRATE', 'fred', start_date, end_date).pct_change().dropna()
unrate = unrate.resample('D').ffill()  # 月次データを日次データに補完（直前の値を保持）
unrate = interporate_df(unrate)
pce = web.DataReader('PCE', 'fred', start_date, end_date).pct_change().dropna()
pce = pce.resample('D').ffill()  # 月次データを日次データに補完（直前の値を保持）
pce = interporate_df(pce)

gt10 = web.DataReader('DGS10', 'fred', start_date, end_date)
gt2 = web.DataReader('DGS2', 'fred', start_date, end_date)
yield_spread = pd.DataFrame(gt10.values - gt2.values, index=gt10.index, columns=['YieldSpread'])
nikkei = stock_info.get_data("^N225", start_date=start_date, end_date=end_date)['close'].pct_change()
# その他指標　適宜利用
#sp500 = web.DataReader('SP500', 'fred', start_date, end_date).pct_change().dropna().squeeze()  # 1次元配列に変換
#nasdaq_composite = web.DataReader('NASDAQCOM', 'fred', start_date, end_date).pct_change().dropna().squeeze()  # 1次元配列に変換
#cpi = web.get_data_fred('CPIAUCSL', start=start_date, end=end_date).resample('D').ffill()

print('unrate\n',unrate)
print('gt10\n',gt10)
print('gt2\n',gt2)
print('pce\n',pce)

# 4. すべてのデータのインデックスを揃える
common_index = nikkei.index.\
        intersection(yield_spread.index).\
            intersection(usd_jpy.index).\
                intersection(pce.index).\
                    intersection(stock_returns.index).\
                        intersection(unrate.index)
# 各データを共通のインデックスに合わせる
nikkei = nikkei.loc[common_index]
usd_jpy = usd_jpy.loc[common_index]
yield_spread = yield_spread.loc[common_index]
pce = pce.loc[common_index]
unrate = unrate.loc[common_index]
stock_returns = stock_returns.loc[common_index]

# 5. 外生変数をまとめる
factors = pd.DataFrame({
    'unrate': unrate.values.squeeze(),  # 1次元配列に変換
    'PCE': pce.values.squeeze(),  # 1次元配列に変換
    'YieldSpread': yield_spread['YieldSpread'].values.squeeze(),  # 1次元配列に変換
    'usdjp': usd_jpy.values.squeeze(),  # 1次元配列に変換
    'nikkei': nikkei.values.squeeze(),  # 1次元配列に変換
}, index=nikkei.index).dropna()  # インデックスを揃えて欠損値を除外
# 外生変数データを1日後ろにシフト（日本市場の株価予測のために前日の外生変数値を使用）
factors = factors.shift(1).dropna()

# 6. インデックスを揃える
common_index = stock_returns.index.intersection(factors.index)
# 両方のデータフレームを共通インデックスに基づいて再サンプリングまたはフィルタリング
stock_returns = stock_returns.loc[common_index]
factors = factors.loc[common_index]
print('factors',factors)
print("stock_returns",stock_returns)
#print("stock_returns.index",stock_returns.index)
#print("factors.index",factors.index)

# 7. データを学習用とテスト用に分割する
y_train_data = stock_returns[:train_end]
y_test_data = stock_returns[test_start:test_end]
X_train_data = factors[:train_end]
X_test_data = factors[test_start:test_end]

# 予測ウィンドウサイズ（１か月、22営業日と想定）
window_size = 22
# テストウィンドウ期間のインデックス
test_start_date = y_test_data.index[0]
test_end_date = y_test_data.index[-1]
# ウィンドウの開始日リストを生成
window_starts = pd.date_range(start=test_start_date, end=test_end_date - pd.Timedelta(days=window_size), freq='22B')
# プロット用の設定
num_windows = len(window_starts)
fig, axes = plt.subplots(nrows=(num_windows+1) // 2, ncols=2, figsize=(14, 4 * (num_windows/2+1)))
print(window_starts)
#print(y_train_data)
#print(X_train_data)
date_format = mdates.DateFormatter('%y-%m')
for i, test_window_start in enumerate(window_starts):
    test_window_end = test_window_start + pd.Timedelta(days=window_size)
    # 各ウィンドウ内のデータを抽出
    y_train_data_window = y_train_data[:test_window_start]
    X_train_data_window = X_train_data[:test_window_start]
    y_test_data_window = y_test_data[test_window_start:test_window_end]
    X_test_data_window = X_test_data[test_window_start:test_window_end]
    #print('y_test_data_window.index\n',y_test_data_window.index)
    #print('X_test_data_window.index\n',X_test_data_window.index)
    # 8. 外生データを使用するモデル
    # モデル定義と学習
    #model = sm.tsa.UnobservedComponents(y_train_data_window, exog=X_train_data_window, level='local linear trend', seasonal=12)
    model = SARIMAX(y_train_data_window, exog=X_train_data_window, order=(1, 1, 1), seasonal_order=(1, 1, 1, 12))
    result = model.fit(disp=False)
    # 学習期間最終株価
    train_last_price = stock_price[:test_window_start][-1]
    #print(stock_price[:train_end].tail())
    print(train_last_price)
    # テスト期間の予測
    forecast = result.get_forecast(steps=len(y_test_data_window), exog=X_test_data_window)
    forecast_mean = forecast.predicted_mean
    #forecast_ci = forecast.conf_int()  # 信頼区間の取得
    forecast_price = train_last_price * (1 + forecast_mean).cumprod() 
    # 予測結果に日付インデックスを追加
    forecast_price.index = y_test_data_window.index 
    print(forecast_price)
    # 9. 外生データを使用しないモデル
    # モデル定義と学習
    #no_exog_model = sm.tsa.UnobservedComponents(y_train_data_window, level="local linear trend", seasonal=12)
    no_exog_model = SARIMAX(y_train_data_window, order=(1, 1, 1), seasonal_order=(1, 1, 1, 12))
    no_exog_result = no_exog_model.fit(disp=False)
    # テスト期間の予測
    forecast_without_exog = no_exog_result.get_forecast(steps=len(y_test_data_window))
    forecast_without_exog_mean = forecast_without_exog.predicted_mean
    forecast_price_without_exog = train_last_price * (1 + forecast_without_exog_mean).cumprod() 
    # 予測結果に日付インデックスを追加
    forecast_price_without_exog.index = y_test_data_window.index 
    print(forecast_price_without_exog)
    # 10. サブプロットに描画
    ax = axes[i // 2][i % 2]
    ax.plot(stock_price.loc[:train_end], label='株価実績値（学習期間）', color='green')
    ax.plot(stock_price.loc[test_start:], label='株価実績値（テスト期間）', color='blue')
    ax.plot(forecast_price.index, forecast_price, label='株価予測値（外生変数あり）', color='red')
    ax.plot(forecast_price_without_exog.index, forecast_price_without_exog, label='株価予測値（外生変数なし）', color='pink')
    ax.xaxis.set_major_formatter(date_format)
    ax.set_xlim(pd.to_datetime('2024-01-01'), pd.to_datetime('2024-10-31'))
    ax.grid(True)
    ax.legend()

# パラメータ推定結果の表示
#print(result.summary())
plt.tight_layout()
plt.show()

コードを実行すると以下のチャートが表示されます。

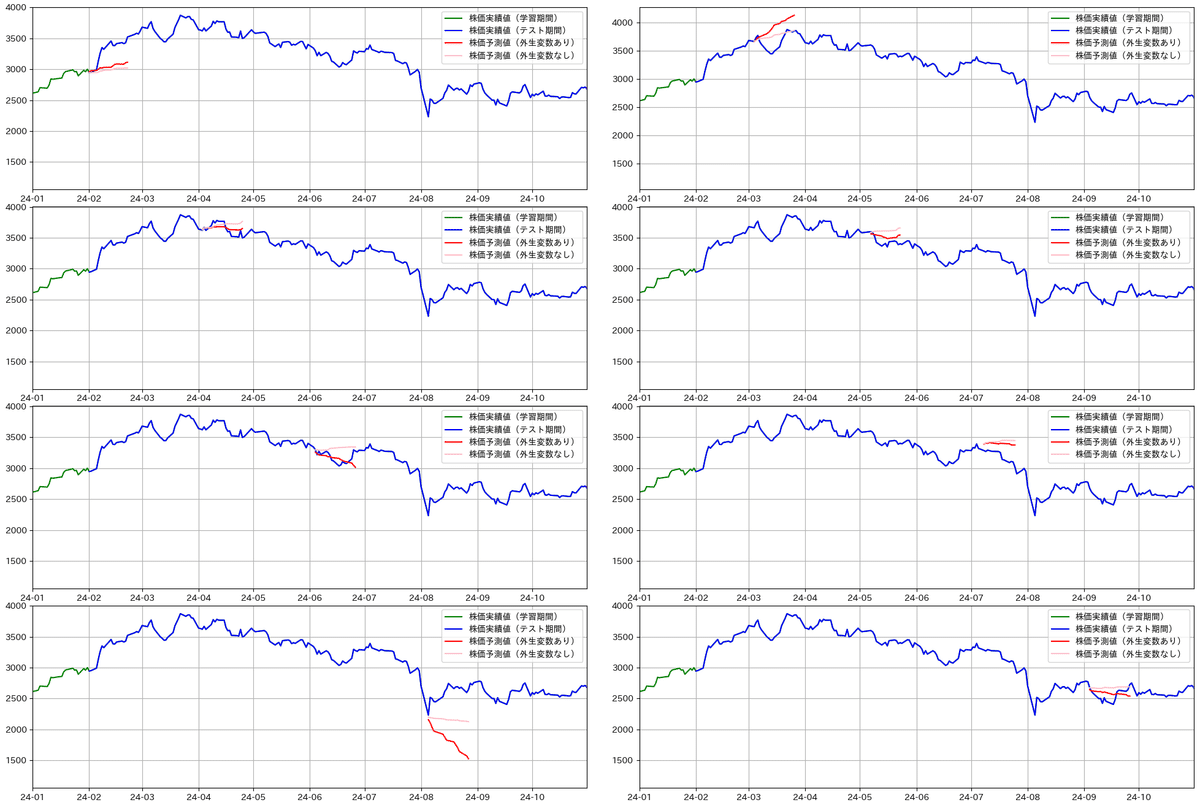
チャートの予測値をみてどう評価されるでしょうか？　4,5,6,7,9月は実績値と割と近い動きをしているように見えます。これに対して2,3,8月の乖離が大きいです。これは以下のように株価に影響を与える明白な材料（ショック要因）があったことによると考えられます。

2月の実績値上昇の背景：2月6日の同社2024年3月期決算が大幅な増収増益の発表があり株価は急上昇しました。　
3月の実績値下落の背景：3月8日発表の米雇用統計の結果ＦＲＢによる早期の利下げ観測により円高・ドル安が進んだ結果自動車株はのきなみ下落しました（参考：日経ＱＵＩＣＫニュース ）。
8月の実績値上昇の背景：これは8月2～5日発生の日経平均株価大暴落の反動での急上昇です。

回帰（AR）やMA（移動平均）は、過去の平均的な挙動を統合して予測を行いますので、雇用や物価のようにマクロ的な数値として積み上げられた指標の分析に適していると思います。一方、株価は、不随意に発生する環境要因や、多数のトレーダーの「読み・思惑」といった数値化の難しいショック要因に強く影響されます。過去データとして振り返って見てしまえば、このコードの時系列処理手法はそれなりに悪くない予測をしているように思えます。しかし、ショックはいつ発生するのかわかりませんので、時系列分析をベースにして株価を予測して実際の取引を行うのは相当リスクがあると筆者は感じます。

ここから先は今後ためしてみたいことです。

マルチエージェントシミュレーション（MAS）という手法があります。これは別稿（Mesaでマルチエージェントシミュレーションを試してみる）で紹介していますのでご一読ください。株式トレードに直接携わる人たちの取引行動をエージェントとしてモデル化したいと考えています。そのために実際の金融・経済指標を外生変数として利用します。この環境の下でエージェントの行動をシミュレートし、エージェントの行動の結果を獲得資産の分布等いくつかの指標を定義して観察してみることに興味があります。

シミュレーションの結果は、現実の株価の予測に役立つかどうかはさておき、なにかおもしろい創発的なパターンが現れるのではないかと想像しています。検討が進んだタイミングでまた別途情報共有していきます。

以上です。