
補足説明 分位数
投稿記事集「数理的手法を使っていろいろ予測したい」のなかで引用した公式や定義、定理類について補足する記事です
分位数とは
確率変数がとりうる値の区間(データセット)を一定の考え方で分割したとき、その分割位置の値を分位数(Quantile)と呼ぶ.よく使われる分割方法には次のものがあります.
中央値:
データセットの中央値(Median)を分位数と決めます。データセットの要素数Nが偶数の場合には中央の値がデータセット内に無いので等分割線の上下2個の値の平均値が中央値になることに注意します.パーセンタイル:
データセットを昇順に並べて100等分してできる分位数をNパーセンタイル(N-percentile)と呼びます.例えば25パーセンタイルはデータセットの 下から25% 以下の境界を指します.
四分位数
NパーセンタイルのNとして25,50,75をとり全データを4区域に分類したときの各区切り線を四分位数といいます.それぞれ第1四分位数,第2四分位数,第3四分位数とも呼びます.簡単なデータセットを例として以下に図解してみました.この図解にある四分位数の決め方は高等学校の指導要領に記載されている方法のようです.
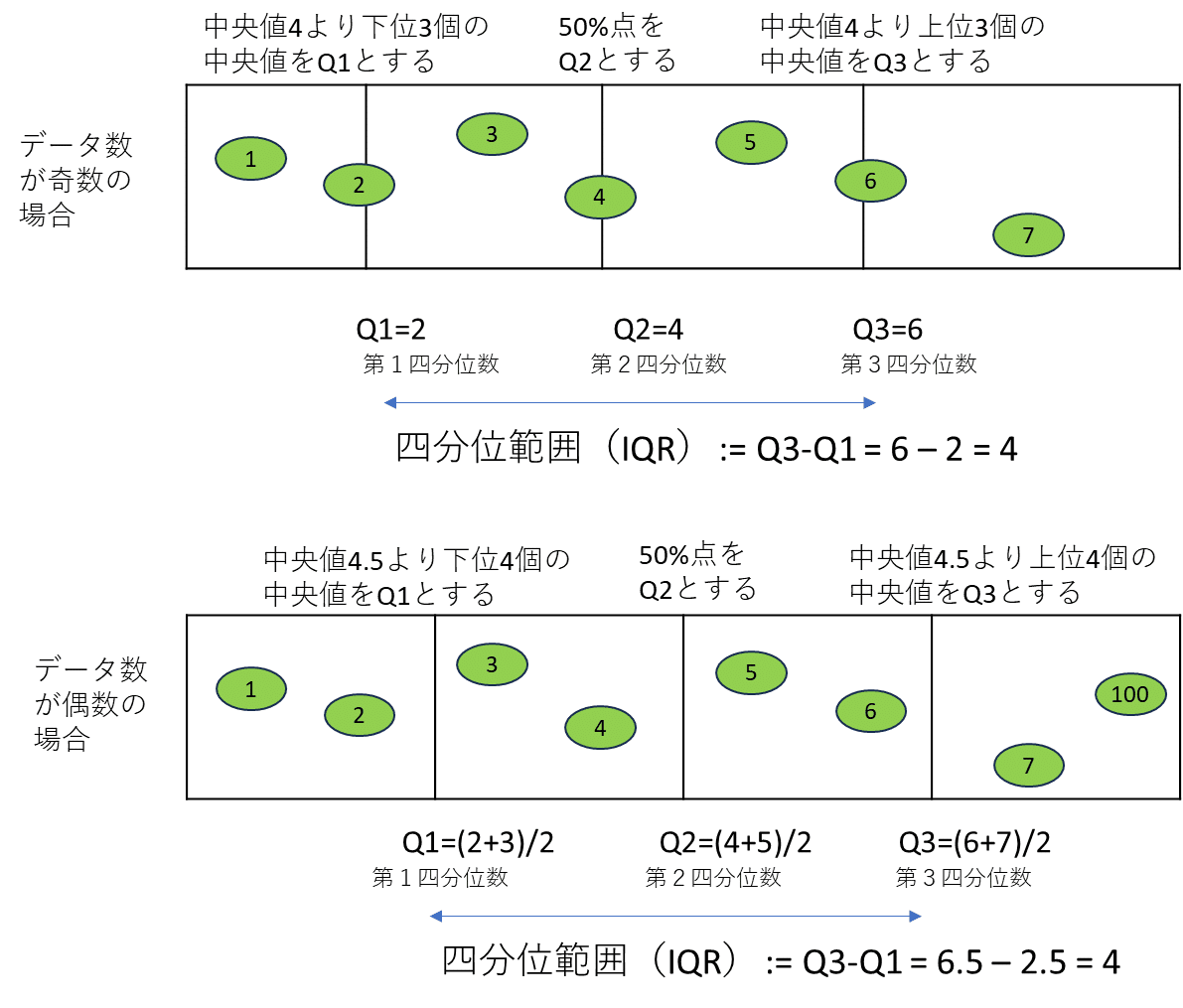
四分位数はデータの外れ値を検出したいときにも利用することができます.例えば以下のようにIQRの1.5倍幅から外れるデータを外れ値とします.
data < Q1 - 1.5 * IQR
data > Q3 + 1.5 * IQR
matplotlibの箱ひげ図(boxplot関数)を使うと,パーセンタイルと外れ値を可視化することができます.
boxplotは,データの第 1 四分位 (Q1) から第 3 四分位 (Q3) まで広がり、中央値に線が引かれた箱(box)を描きます.同時にボックスから四分位範囲 (IQR) の 1.5 倍以内にある最も遠いデータポイントまで伸びたひげ(whisker)を描きます.さらにヒゲの先端を越えたデータポイントを外れ値(outliner)として描きます。以下にサンプルコードと実行した結果を記載します.
# reg_plot_boxplot.py
# docs: https://matplotlib.org/stable/api/_as_gen/matplotlib.pyplot.boxplot.html
import matplotlib.pyplot as plt
import numpy as np
import japanize_matplotlib
np.random.seed(42)
# サンプルデータセットを3グループ生成する
data = [np.random.normal(loc=i*5, scale=1, size=100) for i in range(3)]
# 2個目のグループに外れ値のデータを追加してみる
outliers = np.random.normal(loc=5, scale=2, size=5)
data[1] = np.concatenate([data[1], outliers])
#箱ひげ図をつくる
# notch Trueにすると中央値の信頼性区間を示す窪みを描画する
# vert Trueにすると縦方向に描画する
plt.boxplot(data, labels=['Group 1', 'Group 2', 'Group 3'], notch=False, vert=False)
plt.title('箱ひげ図')
plt.xlabel('値')
plt.ylabel('グループ')
plt.grid(True)
plt.tight_layout()
plt.show()
numpyとexcelのパーセンタイル計算差異
nをデータ配列の要素数、pをパーセント100分率としたときパーセンタイル位置は、前出の高校指導要領の定義はともかくとして
$$
\begin{aligned}
PercentileLocation = (n + 1) * (P / 100) \cdot\cdot\cdot(1)
\end{aligned}
$$
という定義をどこかの資料で読みました.私はこれが定義かと単純に思い込んでいました.これに従うと8要素のデータ[1,2,3,4,5,6,7,100]に対して25パーセンタイル位置は
(8+1)*25/100 = 2.25
実際excelのPERCENTILE関数は(Pが10未満あるいは90超の場合以外は)この値を返します.しかしながらそうはならない定義もあります.numpyにpercentile関数があるので計算してみると、np.percentile(data, 25)は「2.75」を返すのです.
この理由はnumpyの計算式が式(1)ではなく、以下を採用しているからです.
$$
\begin{aligned}
PercentileLocation= (n - 1) * (P / 100) + 1 \cdot\cdot\cdot(2)
\end{aligned}
$$
式(2)を使うとnumpy.percentileが返す値が得られます.
(8-1)*25/100 + 1 = 2.75
式(1)の計算方法はexcelのPERCENTILE.EXC関数と同じで、式(2)の計算方法はexcelのPERCENTILE.INC関数と同じです.ただしPERCENTILE.EXC関数ではパーセンテージの指定が1/(N+1)以下およびにN/(N+1)以上では#NUM!を返します.
データセットの値が小さなレンジと大きなレンジで式(1)を使ってエラーが返るようなケースでは式(2)を用いることでエラーを回避できるところがポイントらしい.
numpyやPERCENTILE.INCでのパーセンタイル定義の図解を以下に示します.前出の定義と比べてみれば相違がわかると思います.

パーセンタイルの定義方法がたくさんできた経緯は良く知らないのですが,データセット数が大きければどの定義でも差異が小さくなるので一貫した使い方をしていればOKということのようです.
正規分布の四分位数
確率変数が標準正規分布に従う場合の四分位数の位置を以下の図で示す.
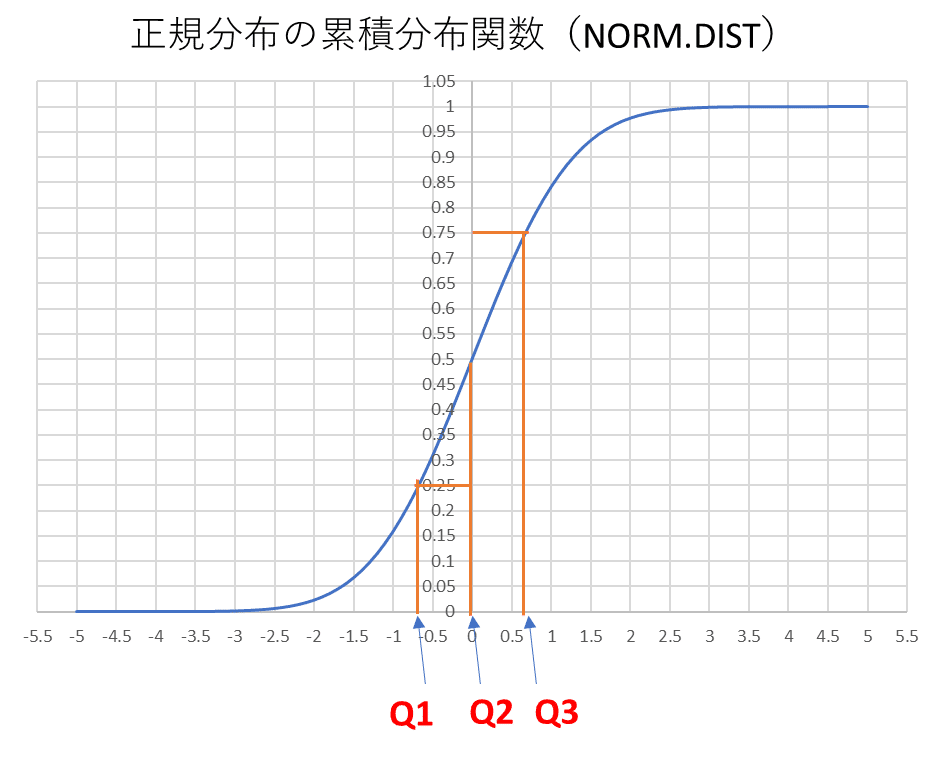
四分位位置の計算は例えばexcelのnorm.inv関数を使うことで簡単に得ることができる.

QQプロット
Q-Q (分位数-分位数) プロットは、指定したデータセットが特定の理論的分布(典型的には正規分布)に従っているかどうかを評価するためのツールです.理論的分布の分位数を横軸に、残差の分布の分位数を縦軸とした散布図を描きます.
以下に簡単なイメージを書いてみました.分位数の位置の比較を図示することで観測データの分布関数と理論的分布関数の差異を視覚的に理解することに役立つと思います.
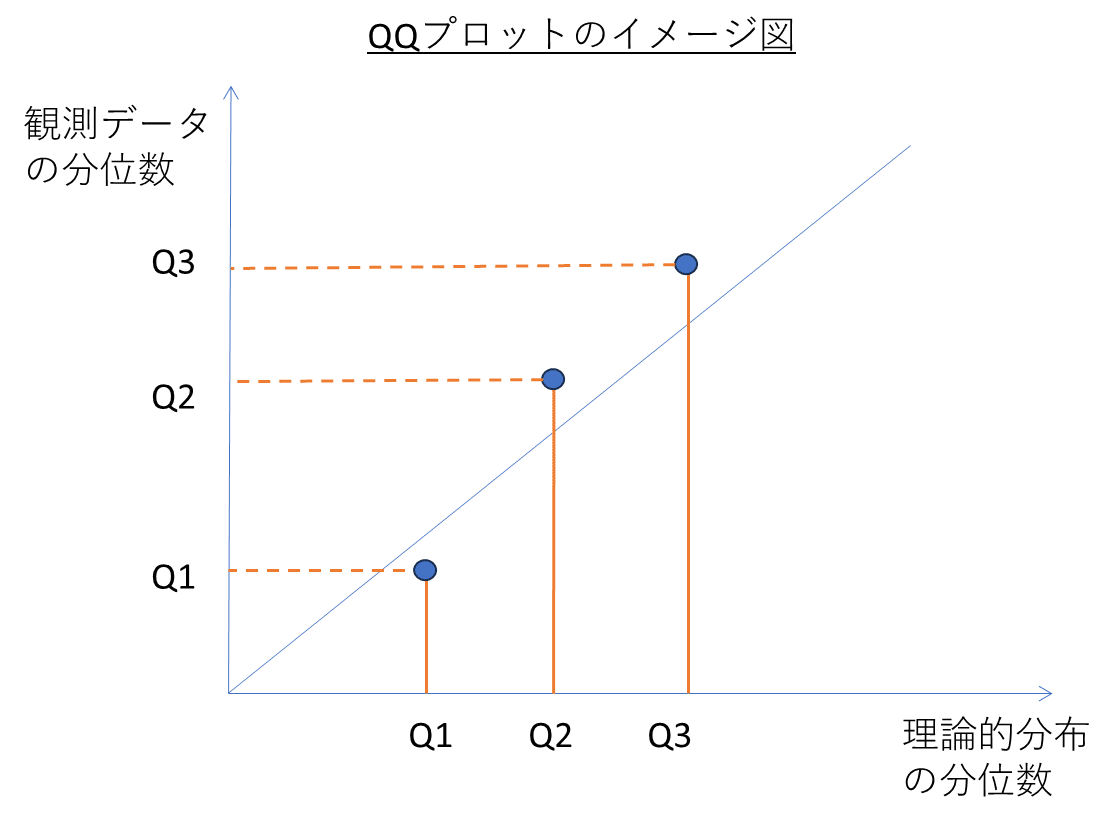
statsmodelsのqqplot関数を例として、プロットの特徴を説明します.
API参照先:statsmodels.api
statsmodels.graphics.gofplots.qqplot(
data,
dist=<scipy.stats._continuous_distns.norm_gen object>,
distargs=(),
a=0,
loc=0,
scale=1,
fit=False,
line=None,
ax=None,
**plotkwargs)dataは標本データを格納した一次元配列.
distは比較の元になる理論的分布です.省略すると標準正規分布が使用されます.
distargs,a,loc,scaleはfitがFalseの場合にdistへ渡されるオプションです.
fitがFalseで,さらにlineを"45"にセットすると標本データの分布が理論分布に一致しているかどうかをプロットで見ることができます.
fitがTrueの場合,理論分布のパラメータは推定値がセットされます.
lineパラメータの各オプションは以下
"45"
45度の参照用直線をプロットする."s"
xを理論分布の分位数の配列としたとき,標本データの標準偏差m,平均bを算出し,y = x・m + bを参照用直線としてプロットする.標本データが平均b,標準偏差mの理論分布に従っていれば散布図の各点はこの直線上にプロットされることになる."r"
標本データから作成した回帰直線を参照用直線としてプロットする。"q"
第1四分位数と第3四分位数を通る参照用直線をプロットする。
以下にstatsmodelsのサンプルコード(微修正版)を記載します.
# reg_check_plot_longley.py
# slitely modified version of sample program by statsmodels docs.
#
from matplotlib import pyplot as plt
import statsmodels.api as sm
#example from docstring
data = sm.datasets.longley.load()
data.exog = sm.add_constant(data.exog, prepend=True)
mod_fit = sm.OLS(data.endog, data.exog).fit()
res = mod_fit.resid
left = -1.8 #x coordinate for text insert
fig = plt.figure()
# line='45'
ax = fig.add_subplot(2, 2, 1)
sm.graphics.qqplot(res, line='45', fit=True, ax=ax)
ax.set_xlim(-2, 2)
top = ax.get_ylim()[1] * 0.75
txt = ax.text(left, top, "line='45', \nfit=True", verticalalignment='top')
txt.set_bbox(dict(facecolor='k', alpha=0.1))
# line='s'
ax = fig.add_subplot(2, 2, 2)
sm.graphics.qqplot(res, line='s', fit=False,ax=ax)
top = ax.get_ylim()[1] * 0.75
txt = ax.text(left, top, "line='s', \nfit=False", verticalalignment='top')
txt.set_bbox(dict(facecolor='k', alpha=0.1))
# line='q'
ax = fig.add_subplot(2, 2, 3)
sm.graphics.qqplot(res, line='q', fit=True,ax=ax)
top = ax.get_ylim()[1] * 0.75
txt = ax.text(left, top, "line='q', \nfit=True", verticalalignment='top')
txt.set_bbox(dict(facecolor='k', alpha=0.1))
# line='r'
ax = fig.add_subplot(2, 2, 4)
sm.graphics.qqplot(res, line='r', fit=True,ax=ax)
top = ax.get_ylim()[1] * 0.75
txt = ax.text(left, top, "line='r', \nfit=True", verticalalignment='top')
txt.set_bbox(dict(facecolor='k', alpha=0.1))
fig.tight_layout()
plt.show()
結果のプロット

---
