2020年東京大学理系第5問
こんにちは。しろ@です。
自分が受験した年の受験校の問題を全部取り上げるシリーズ第1弾(東大)、今回は2020年東京大学理系第5問です!
問題
問題は次の通りです。
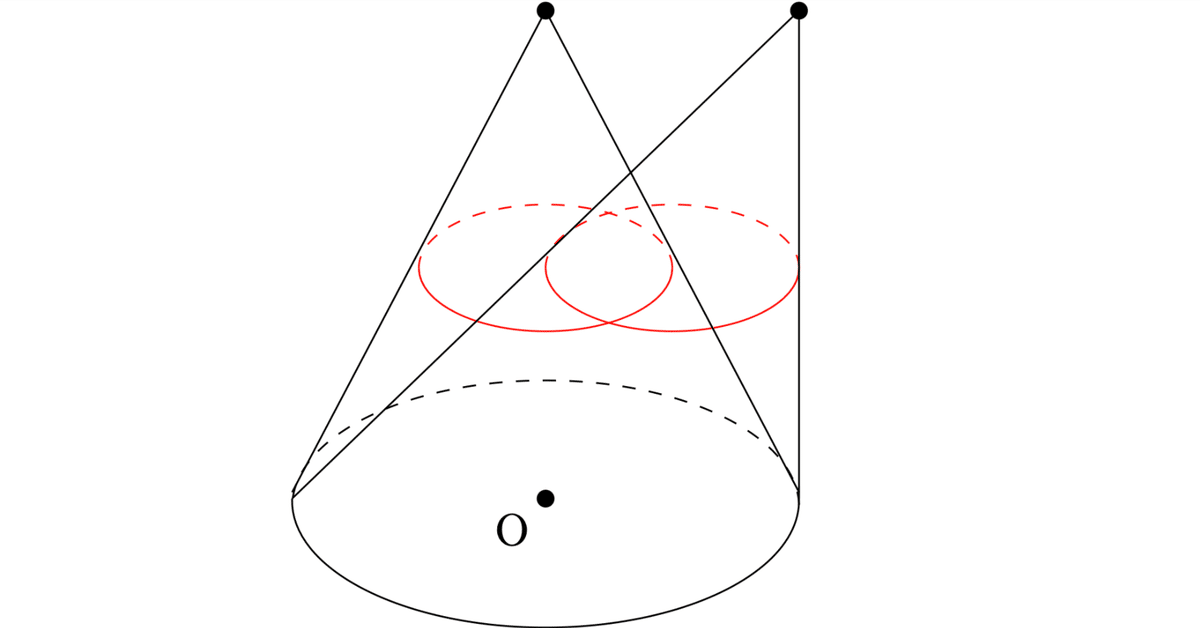
座標空間において、$${xy}$$平面上の原点を中心とする半径$${1}$$の円を考える。この円を底面とし、点$${(0, 0, 2)}$$を頂点とする円錐(内部を含む)を$${S}$$とする。また、点$${\mathrm{A}(1, 0, 2)}$$を考える。
(1) 点$${\mathrm{P}}$$が$${S}$$の底面を動くとき、線分$${\mathrm{AP}}$$が通過する部分を$${T}$$とする。平面$${z=1}$$による$${S}$$の切り口および、平面$${z=1}$$による$${T}$$の切り口を同一平面上に図示せよ。
(2) 点$${\mathrm{P}}$$が$${S}$$を動くとき、線分$${\mathrm{AP}}$$が通過する部分の体積を求めよ。
サムネにする数式がないではないか!$${\LaTeX}$$で何か描くか…でも立体だしな…いやそんなことはどうでもいい。
問題の状況設定は次のようになっています。

まず、(1)です。$${\mathrm{P}}$$が$${S}$$の底面を動き回るとき、$${S}$$は$${\mathrm{B}(0, 0, 2)}$$を頂点とする円錐で、$${T}$$は$${\mathrm{A}(1, 0, 2)}$$を頂点とする円錐もどきになります。これらの立体の平面$${z=1}$$による切断面を求めます。これは簡単にイメージできると思います。
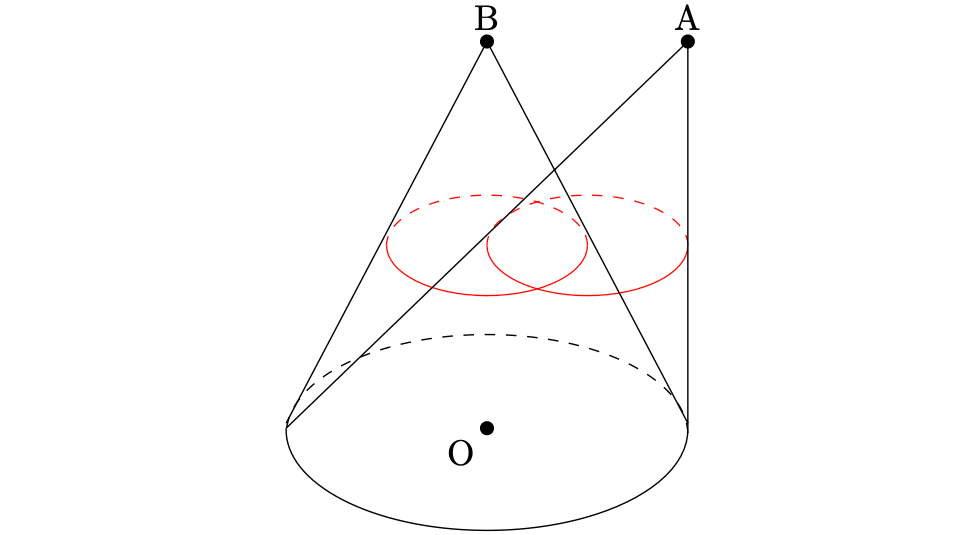
これで解答でもよいのですが、ちょっと直感的すぎます。計算で求められるなら計算しておきましょう。
(2)は、$${\mathrm{P}}$$が$${S}$$全体を動き回ります。$${z=k\quad(0\leqq k\leqq2)}$$による切断面を求めて、$${k=0}$$から$${k=2}$$まで積分すればよいのですが…
解答


解説
いかにも東大らしい問題(イカ東)!積分で体積を求める問題は、教科書だと回転体ばかり扱われて、断面積を積分するタイプの問題は最初にちょっとやるだけで蔑ろにされがちなイメージ。
(1)の解答を詳しく書きすぎてしまったので全体として長くなってしまいました。というわけで、まず、(1)から。方針としては次のようになります。
$${\mathrm{P}}$$の座標をパラメータを使って表す。
直線$${\mathrm{BP}}$$と直線$${\mathrm{AP}}$$の方程式をそれぞれ求める。
その方程式に$${z=1}$$を代入して切り口の方程式を求める。
まず、$${\mathrm{P}}$$の座標を設定します。$${S}$$は$${xy}$$平面上の単位円の周と内部なので、極座標の考え方を使って、
$$
\mathrm{P}(r\cos\theta, r\sin\theta, 0)\quad(0\leqq r\leqq1, 0\leqq\theta<2\pi)
$$
と書けます。続いて、直線$${\mathrm{BP}}$$と直線$${\mathrm{AP}}$$の方程式を求めます。ベクトルを使って直線の方程式を求めるときは、①通る点の座標、②方向ベクトルの2つとパラメータが1つ必要になります!
さて、最後に$${z=1}$$を代入します。そうすると直線の方程式を求めるときに出てきたパラメータが1つに決まります。これを代入すると、$${x, y}$$が2つのパラメータ$${r, \theta}$$で表されます。$${\sin^2\theta+\cos^2\theta=1}$$を用いて$${\theta}$$を消去すると、$${r}$$を残して$${x, y}$$が1つの式にまとまります。あとは$${r}$$を$${0\leqq r\leqq1}$$で動かせば完了です。
さて、肝心の(2)です。体積を求める問題は東大では頻出です。基本的な考え方は、平面$${z=k}$$による断面積(あるいは$${x=k}$$や$${y=k}$$など)をパラメータ$${k}$$が動く範囲で積分する、です。したがって、まずは平面$${z=k}$$による断面積を求めます!さすがに$${x=k}$$や$${y=k}$$はないかな。円錐を縦に切るのはちょっと…
断面積の求め方の方針は、(1)で挙げた3点と同じです。まず、点$${\mathrm{P}}$$の座標を設定したいのですが、今回は$${z}$$座標も動くので、必要なパラメータがたくさんあります。具体的には、
$$
\mathrm{P}(r\cos\theta, r\sin\theta, p)\quad\left(0\leqq r\leqq\displaystyle\frac{2-p}{2}, 0\leqq\theta\leqq2\pi\right)
$$
と書けます。$${r}$$の上限値は相似比を使えば簡単に求められます。問題なのは$${p}$$の動く範囲です。今回は$${z=k}$$による断面積を考えているので、$${p>k}$$だと直線$${\mathrm{AP}}$$は$${z=k}$$と交点を持ちません。したがって、$${p}$$の動く範囲は$${0\leqq p\leqq k}$$となります!
$${\mathrm{P}}$$の座標が設定できたので、直線$${\mathrm{AP}}$$の方程式を求めます。これは(1)と同じです。ここでもパラメータ(解答では$${u}$$)が出てくるので、必要になるパラメータは$${k, r, \theta, p, u}$$の合計5個です。超いかつい。それぞれの動く範囲を明確にすることが重要です!
直線の方程式が分かったので、$${z=k}$$を代入します。パラメータがごちゃごちゃしすぎて訳わからないので、(1)でやったことをなぞっていきましょう。そうすると、$${u=\displaystyle\frac{2-k}{2-p}}$$に決まります。
これを代入すると、$${x, y}$$が$${k, r, \theta, p}$$で表せます。次に、$${\sin^2\theta+\cos^2\theta=1}$$を用いて$${\theta}$$を消去すると、$${x, y}$$が$${k, r, p}$$を残して1つの式にまとまります。具体的には、その方程式はある円を表します。
さらに、$${0\leqq r\leqq1}$$より円の周と内部(円板)を表すことが分かり、$${0\leqq p\leqq k}$$より円板が$${x}$$軸に平行に動きます。半径は変わらないのでラッキー。
あとは断面積を求めればオッケー!パラメータ$${k}$$だけを残して表現できます。最後のお仕事はその断面積を$${k=0}$$から$${k=2}$$まで積分すること。ただの多項式の積分なので簡単に求められます。
最後にコメント
(2)は結構大変でしたねー。個人的な難易度は「やや難」です!標準とするものも多い気がしますが。第4問、第6問に次ぐ難しさがあると思います。合格者平均をとる受験生なら完答できるレベルかな。$${\mathrm{P}}$$が円錐内全体を動くので座標設定するのが難しく、$${z=k}$$と線分$${\mathrm{AP}}$$が交点を持たなければならない点を考慮するのも大変です。
自分が受験したときは、(2)の断面積の形状を間違え(具体的には、(1)のような円板2つの合併だと思ってしまった)てしまい、$${z=k}$$における断面積を求めることができずにそこで断念する形となった気がします。
積分で体積を求める系の問題は東大では頻出なので、東大受験生にとっては良い訓練になると思います。これくらいの問題が解けたら、この類の求積問題には自信を持っていいと思います。
今回はここまで。次回は2020年東京大学理系第6問を取り上げます!いよいよ最後の問題ですね。東大の次は早稲田にしようかな…慶應にしようかな…
最後までお読みいただきありがとうございました。もしよろしければ、次回以降の記事もお読みいただけると嬉しいです。
それでは、また次の記事で。
2024.02.23
しろ@
