ハッピーな数？―数たちの知られざる性質―

こんにちは。和からの数学講師の岡本です。みなさんは数を見て「ハッピーだ！」なんて感じることありますか？僕はあります。例えば、不意に目に入った数が素数だったらなんだかうれしいです

その他にも、ロマンティック数学ナイトのプレゼン時間でおなじみの「完全数」。（完全数とは、その数以外の約数を全て足し和わせると元の数に一致するような特殊な数です。弊社で開催している数学のプレゼン交流会「ロマンティック数学ナイト」の一人当たりのプレゼン時間は３番目の完全数である496秒を採用しています。）

このような「特別な性質」を持った数には特別な感情を抱きます。今日ご紹介するのは、「ハッピー数」と言われる数についてです。名前からしてハッピーですね！一体どんな数なのでしょうか！

１．ある操作

まず、皆さんになんでもいいので数を一つ選んでもらいます。例えば57など、なんでも構いません。次に選んだ数の各桁の数を全て２乗してあげます。57を選んだ場合、5と7をそれぞれ２乗して25と49を値作り出します。その後、それらの数を足し合わせます。57を選んだ場合、25+49=84となります。この操作で数57は、新しく84へと移り変わりました。以下、この操作のことを「𝐹₂」と書くことにします。

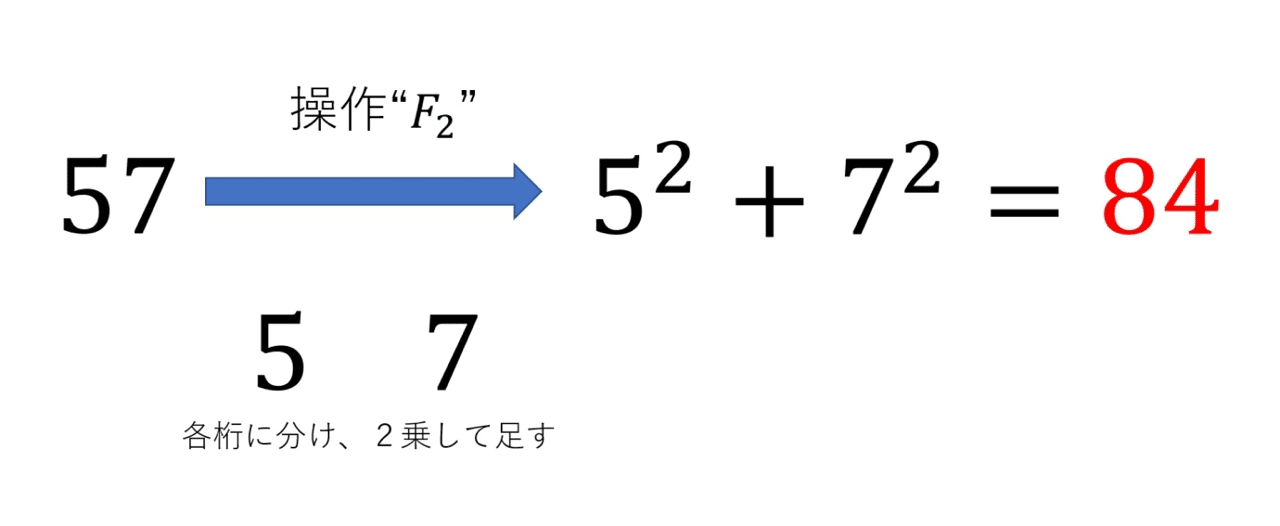
続いて今の操作𝐹₂をもう一度繰り返します。つまり、84に対してもう一度同じ計算を行います。8と4の２乗の和は64+16=80となり、84は80へと移ります。

みなさんはこの操作𝐹₂をずーーーっと繰り返してみてください。初めに57を選んだので、このまま続けていきます。

２．行き着く先は？

いかがでしたか。ずーっと続けると「あるパターン」に陥ると思います。57を選んだ場合、操作𝐹₂を続けると4に移りました。その後操作を続けると16, 37, 58, 89,…となり、途中に現れた、89に戻ってきました。つまり、「無限ループ」に陥ってしまったのです。

もしかするとこの操作を行って1になった方もいらっしゃるかもしれません。例えば23を選ぶと、4+9=13, 1+9=10, 1+0=1となり、１度1に到達してしまうとそこから動きません！つまり、「ゴール」にたどり着いたのです。

実はどんな数でも、「各桁を２乗して足す」という操作を繰り返していくことで、「4を含むサイクル」に陥るか、「１」に到達するかの２通りしかないことが知られています！

何度か操作𝐹2を施して「１」というゴールにたどりつく数のことを「ハッピー数」といいます！実際、ほとんどの数が「４を含むサイクル」に陥てしまうので、ある意味「１」にたどり着く数は“貴重”なのです。こういった意味で「ハッピー数」と名前が付けられています。

３．２通りしかないことの証明

前節では「４を含むサイクル」に陥るか、「１」に到達するかの２通りしかないという驚くべき結論をご紹介しましたが、やはりなぜなのか気になりますよね。ここで簡潔にその証明をしていこうと思います。

→続きはこちらから

岡本の数学アート作品、デザイングッズはこちらから

和からではご自身のペースで学びたいことを学びたいだけ学ぶことができます。算数や数学の苦手意識克服、お仕事で使う計算から実務に役立つデータ分析まで、幅広く対応いたします。ご興味がある方はぜひ一度無料セミナー、無料個別カウンセリングにご相談ください。

<文/岡本健太郎>