
美しきタイリングの世界~鬼滅の刃やエヴァンゲリオンでも使われる幾何学模様~
今回は「タイリング」の美しさについてお話していきます。街を歩いてみると、そこら中に「模様」があふれかえっています。街だけでなく、大人気漫画「鬼滅の刃」、「新世紀エヴァンゲリオン」などにも、多くの美しい幾何学模様が使用されています。今回はこれらの模様について詳しく見ていきましょう。
この記事の主な内容
1.模様のパターンを楽しむ
2.作り手の気持ちを考える
3.数学を使って考えることができる
4.さいごに
1.模様のパターンを楽しむ
街に出ると様々な模様に出会うことができます。たとえば、壁の装飾など。

東京駅の改札口を見上げると。

レンガ造りは繰り返し模様となっています。

模様を楽しむオススメスポット「東京ジャーミィ」。

どれも美しいですね!
2.作り手の気持ちを考える
では、次に模様を作る側の視点で考えてみましょう。上でみたタイリング(=平面に敷き詰めること)や繰り返し模様というのは、全て1から描いているのでしょうか?そんなことはありません。一部を描き終えたあと、「繰り返す」ことによって模様が描かれていきます。レンガもそうで、その都度形に合うレンガを作るのではなく、最初から同じ大きさのレンガ(コピー)を使って一気に組み上げていくのです。例えば、正方形をコピーすることで、「格子模様」が出来上がります。2色で色分けを行えば、市松模様と呼ばれる模様になり、現在人気爆発中の漫画「鬼滅の刃」における主人公・炭次郎のトレードマークとして話題になっています。
ちなみに、「市松模様」とは、江戸時代の人気歌舞伎役者「初代佐野川市松」のファッションから名前が付いています。当時のファッションリーダーだったようです。また、同じく江戸時代に女性の間で流行した「麻の葉模様」というものもあります。これは正三角形がベースで非常に美しい模様となっています。こちらも漫画「鬼滅の刃」の主人公の妹・禰豆子のトレードマークとなっています。
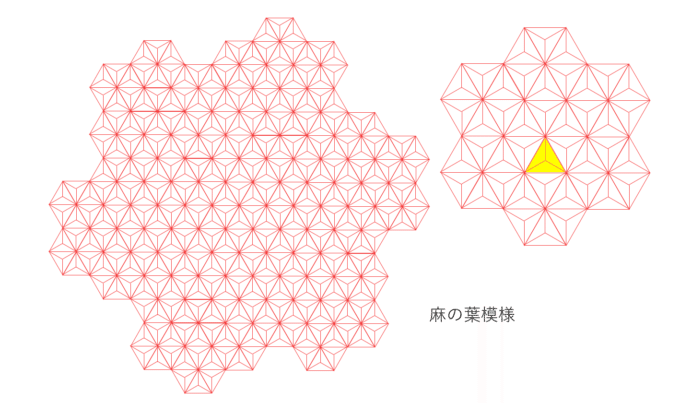
麻の葉は生命力が高いので縁起物として子どもの着物にも使われました。
しかし、どんな形でもきれいにタイリングできるのでしょうか?例えば、正五角形だとどうでしょうか?
3.数学を使って考えることができる
正方形や正三角形はタイリングできますが、実は正五角形ではうまくタイリングできません。図のように角度が合わなくなってしまいます。このように「タイリング」というものをすこし考えてみると、「タイリング可能な形」と「タイリング不可能な形」に分かれることに気が付きます。

では、正多角形のみで考えると、どんな図形がタイリング可能でしょうか?
これには、簡単ではありますが数学が関連してきます。その数学的な考察を行えば、タイリング可能な正多角形は、なんと「正三角形」「正方形」「正六角形」のみであることがわかります。

数学っておもしろいですよね!こんなこともわかっちゃうのですから!
なお、正六角形のタイリングは「ハニカム構造」と呼ばれ、以前マスログで解説いたしました。興味のある方がご覧ください。
さらに、この正六角形のタイリングは様々なデザインとして利用されています。漫画「鬼滅の刃」でも数多く登場しますし、今月映画公開予定(だった)の「エヴァンゲリオン」の作中でも、正六角形のタイリングが多く現れます。ぜひ注目してみましょう!(敵に正八面体も登場します)

4.さいごに
いかがでしたでしょうか?今回は日常の様々な模様や、繰り返りのタイリングについて簡単にご紹介してきました。次回はタイリングについてもう少し考察し、多角形のタイリングの数学的な説明を紹介していきます。
和からでは、こうした「数学的なデザイン」の捉え方や考え方に関するセミナーを開催しております。興味のある方は是非ご参加ください!
漫画で模様を探してみるのもおもしろいかもしれません。
新世紀エヴァンゲリオン 貞本義行(著) KADOKAWA
鬼滅の刃 吾峠呼世晴(著) 集英社
<文/岡本健太郎>
