
久留米大学附設中2024年度入学試験算数について講評および解説
2024年度に行われた久留米大学附設中入試の解答解説をざっくりですが、作成しました。
問題PDFについては以下、四谷大塚のサイトからダウンロードしてください。
講評
大問1
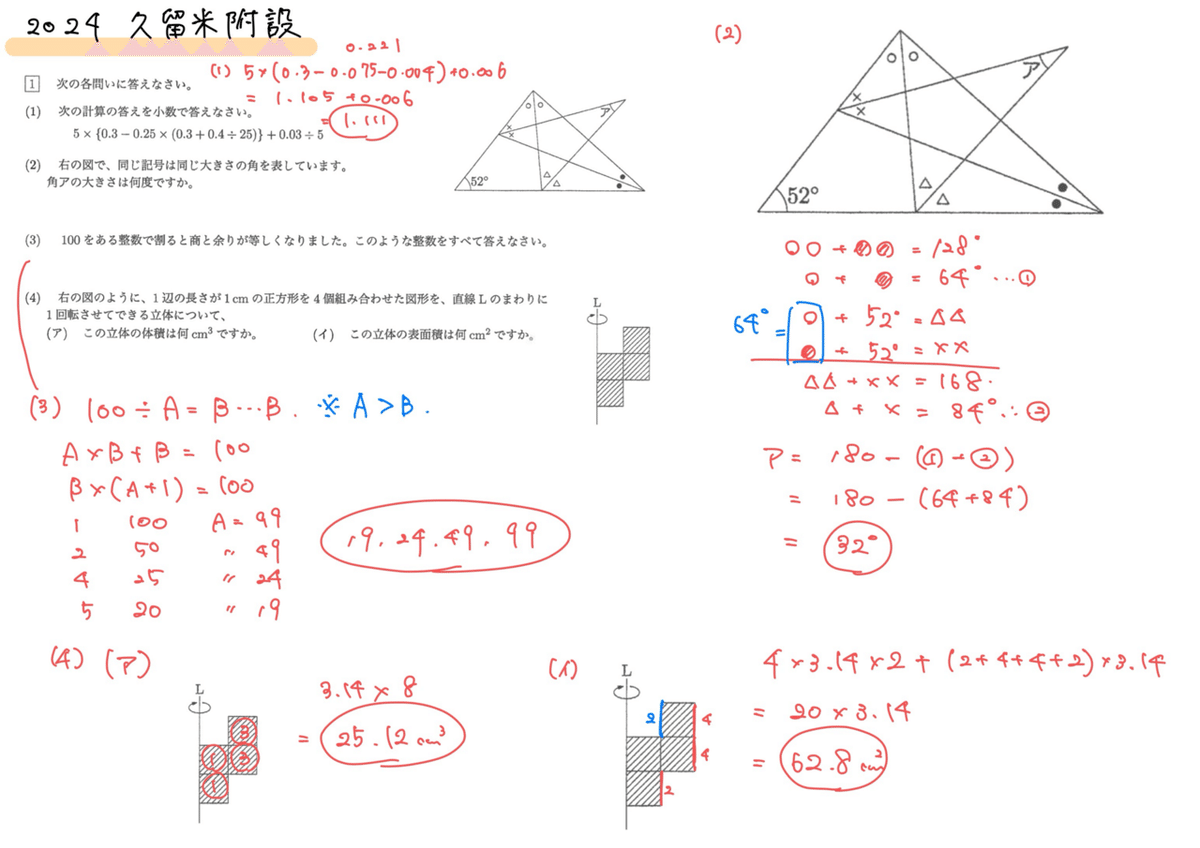
小数で答える計算問題から始まり、回転体など図形が絡む問題も散りばめられている。(2)の角度の問題をできるだけスピーディーに解きたい。また(3)の問題は漏れなく確実に完答したい問題だった。
大問2

うるう年についての問題。(1)は正答率がかなり高いと予想される。(2)も2100年を除外することに注意すれば難なく正解できる。(3)は丁寧に筆算を行うこと、また閏年を考慮することに注意する。
大問3
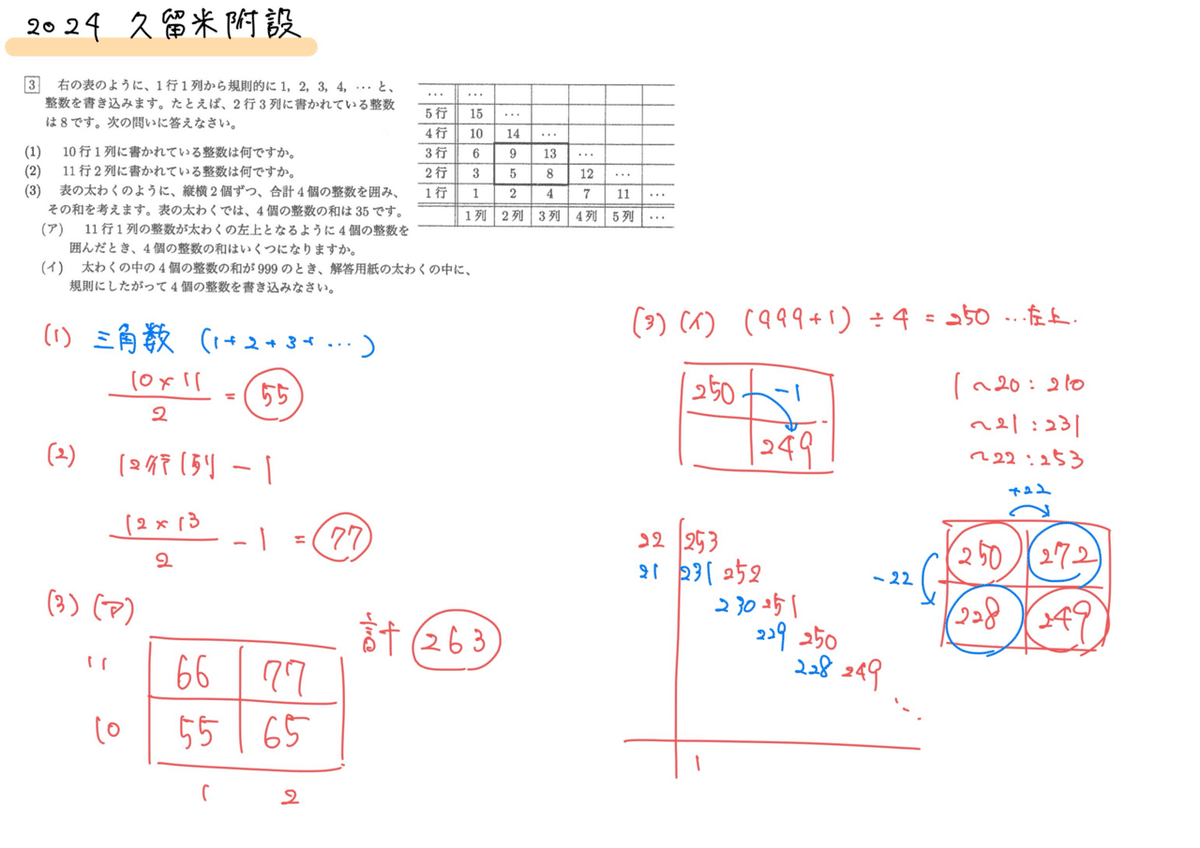
三角数が表に並べられた問題。(1)(2)は難しくないので確実に正解したい。(3)の(ア)も(1)(2)の答えを利用すれば比較的スムーズに解答までたどり着ける。(イ)については地道に『○行1列』の数字を調べて辿っていく。
大問4
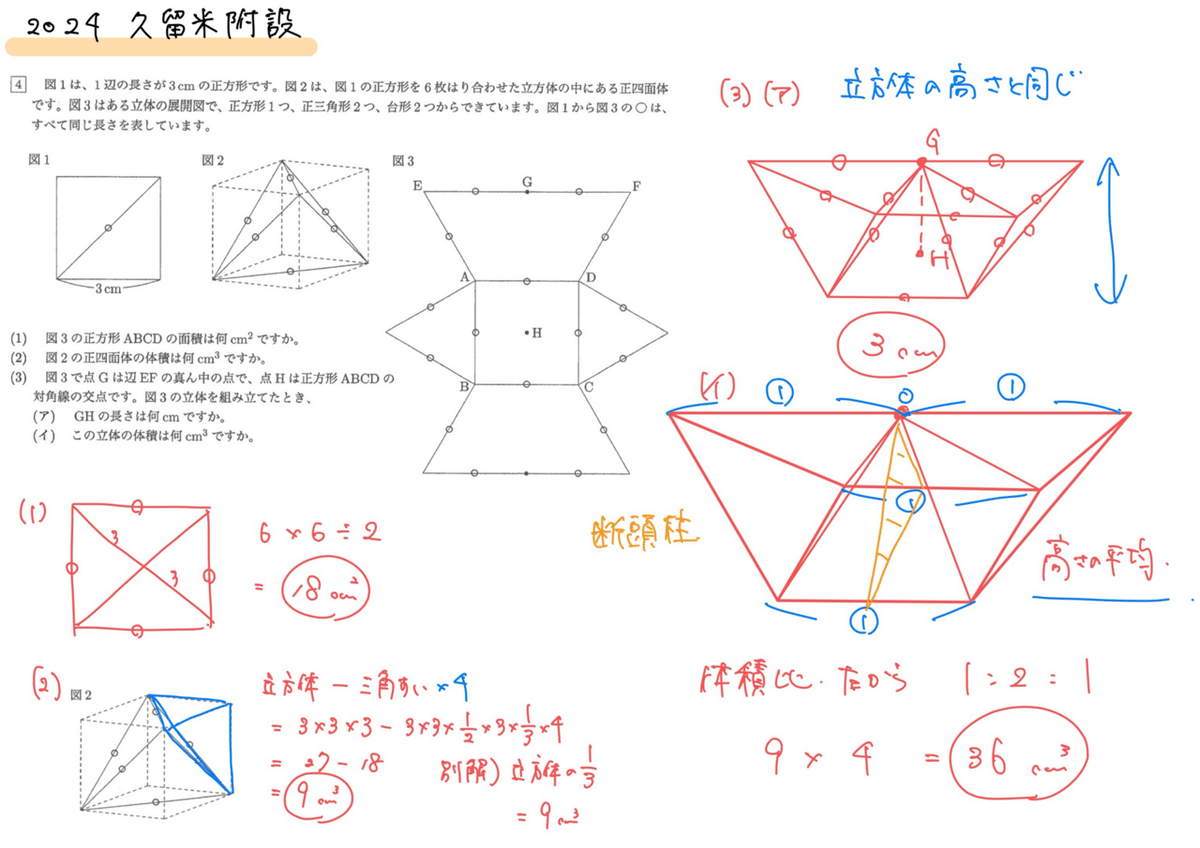
空間図形についての問題。(1)は正方形の面積="対角線×対角線÷2"を利用して解く。慌てていると誤答する可能性あり。(2)は立方体の3分の1で瞬殺。(3)(ア)図2の立体と同じ立体に気づければ瞬殺。(3)(イ)は断頭柱体の体積の求め方(『断面積×高さの平均』)を使う。真ん中の正四角すいが両端の正四面体の2倍の体積になっている。
大問5
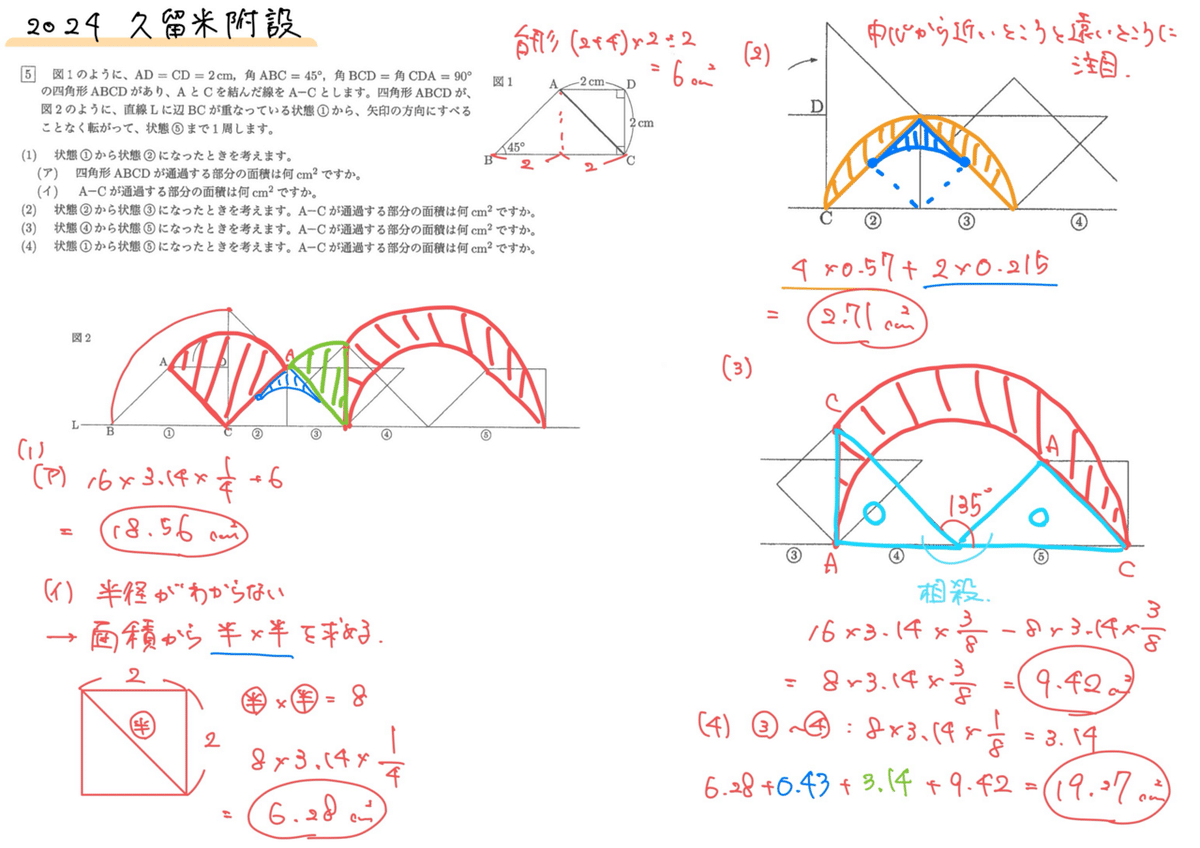
図形の回転移動についての問題。難易度がずば抜けて高い設問はない。(1)〜(4)まで丁寧に作図しながら解いていく。一点ポイントとしてはおうぎ形の面積を求める際の『半径×半径』を正方形の面積を利用して出すこと。
以上、ご参考までに。間違いがあればご指摘ください。
