
【マーケティング基礎】ABテストの全体像をわかりやすく
はじめに
ビジネスにおいて何らかの施策を行った時、効果があったかどうかを検証するシーンは数多くあると思いますが、そんな時にABテストは非常に役に立ちます。セールスやマーケティングなどの分野では頻繁にABテストは用いられていますし、それ以外の分野でも幅広く活用できる手法だと思います。
完全な理解のためには統計理論の理解も必要ですが、本稿では活用用途をはじめとした全体像を正しく理解することにフォーカスし、統計や数学的な説明は最小限にしてわかりやすく説明していきたいと思います。
ABテストとは何か?
ABテストとは2つ以上の施策を同時並行で実施し、どちらが効果があったかを統計的裏付けをもって検証する手法で、様々なシーンで活用されています。例えば、ネット広告などで「表現を一部変えたもの」と「変えていないもの」をランダムにユーザーへ表示し、どちらが高い効果が得られるかを検証する、といったかんじです。

医療の世界でも使われていて、エビデンスレベルでもかなり高い検証手法とされています。

なぜABテストが必要?
ざっくり言えば「どっちの施策がイケているかを統計的根拠をもって判定したい」という場面で必要です。
例えばメールマーケティングのレスポンス率を比較する検証があったとします。 テキトーにピックアップした2つの集団に対して「文面A」「文面B」それぞれ送りました、と。
「文面A」は2%、「文面B」は3%のレス率でした。
「よっしゃ!文面Bの方が効果があったので、次回もこれでいこう!」
でもこれって「たまたま偶然Bが良かった」という可能性はありませんか?
もし偶然だったら、誤った意思決定をしてしまいます。そうならないように「偶然ではない、意味のある差があった」ことを裏付ける根拠があると安心感・納得感のある「正しい」意思決定ができるようになります。その根拠のためには統計的なアプローチが必要になります。
どんなメリットがあるか?
まず、「着実な改善の積み重ねができる」ことが挙げられます。
ABテストによって「何を変えるとどのくらい効果が改善されるか」が明確になるので、成功したパターンを更にABテストし、そこで成功したパターンをABテスト、、、と繰り返していくことにより、ブラッシュアップしていくことが可能になります。
次に、「複数パターンを同時並行で比較検証できる(工夫すれば)」という点もメリットです。
ABテストはテストパターンを工夫すれば複数パターンを一度に検証できます。すなわち、ABテストの試行回数が増えるため、改善に要するリードタイムの短縮が可能です。
理解が必要なポイント
ABテストを理解するのに必要なポイントは以下の4つです。
無作為抽出(ランダムサンプリング)
サンプルサイズ設計
テストパターン設計
有意差の検定
無作為抽出(ランダムサンプリング)
ABテストは比較する集団(テストグループ)がそれぞれランダムである必要があります。なぜか?それは各グループの属性の偏りを排除するためです。
例えば、メールマーケティングで2,000人に対して、1,000人ずつ2グループに分けてレスポンス率のテストをするとします。ターゲットとなる人達は様々な属性を持ってます。性別、年代、居住地、職業、役職、メールをみる習慣の有無、、、、挙げればキリがありません。これら無数の属性ごとに反応率が変わってくる可能性があります。
例えばメールをみる習慣がない人よりもある人の方がレス率は高くなるかもしれないし、職業によっても違いがあるかもしれません。もし2つに分けたグループの片方に、レスに有利な属性が偏っていた場合(=その属性の構成比が高かった場合)、メールの内容を変えたことによる効果なのか、そもそも属性の偏りによる効果なのかが判断できません。
これではABテストが成り立たないのです。では、どうすればいいか?
すべての属性を調査して、各属性が均等な構成比になるように調整できればいいですが、現実的にはすべての属性を洗い出すことは絶対にムリです(属性は無数にあるわけですから)そこで、無作為抽出(ランダムサンプリング)という手法を用います。
無作為抽出されたグループは、すべての属性の構成比が、母集団の構成比とほぼ一致します。一致の度合いは抽出するサンプル数(サンプルサイズ)が多いほど高まります(詳細は後述)
どうやって無作為抽出を行うかについては、どのツールを使うかにもよりますが、例えばExcelリストで行うことも可能です。具体的な手順についてはこちらの記事を参照してもらえれば分かると思います(とても簡単です)
個人的には、母集団から無作為抽出したグループは母集団の「把握できていない」全ての属性まで全て同じ構成比になっているという点が実に不思議で、初めて無作為抽出したリストを眺めた時にとても感動したのを覚えています。
なぜそうなるのかは理論の理解が必要ですが、例えば水に食塩を入れてめちゃくちゃ混ぜたら、その水全体の濃度と、そこから少量だけ取り出した水の濃度はほぼ同じになりますよね?それと同じようなものです(たぶん)そういうもんだと理解しておけば十分です。
サンプルサイズ設計
サンプルサイズとはサンプルの数のことです。
例えば、ある商品の販促メールを顧客へ一斉配信する施策が企画していたとします。商品の製造リードタイムや在庫なども考慮すると、この販促によって一気に注文がくると対応できないリスクがあるため、まずはどのくらい反響(配信数に対する受注率)があるかを見極める必要がある、と考えました。
以前、別の商品で販促メールを送った時は受注率1%だったというデータがあります。今回もおそらく1%前後の反響があるんじゃないかとは思うものの、できるだけ正確に把握したい。
受注率がどのくらいか確かめるためには、どのくらいの配信数(サンプルサイズ)があれば問題ないでしょうか?
なんとなく「多ければ多いほど精度は高い」と思う人が多いのではないでしょうか?実はそれは正解でもあり、不正解でもあります。

このグラフはコイントスで表が出る確率を、試行回数を増やし続けた場合にどうなるかを示したものです。表が出る確率は50%ですが、試行回数が少ないうちは50%からかなりブレているのがわかります。
なぜか?それは「偶然」の影響を受けてしまうからです。
理屈上は2回中1回は表になるはずですが、偶然の影響で0回(0%)の場合もあるし、2回(100%)の場合も発生しますよね。しかし、試行回数を増やし続けると、徐々にその確率は50%へ収束する性質があります。これを「大数の法則」といいます。
見ての通り、ある一定数に達するとほぼ50%に収束し、それ以降は試行回数を増やしても精度はほとんど変わらなくなります(ちなみに試行回数ではなく、一度にトスするコインの数に置き換えても同じ結果になります)
この例ではサンプルサイズ=(試行回数 or コインの数)と捉えて下さい。よくみると、この50%を基準に上下にぶれている誤差が、サンプルサイズが増えていくにつれて小さくなり、次第に収束していくことが分かります。
つまり、サンプルサイズが増えるほどに誤差は0に近づいていく性質があるのです。逆に言えば、表の出る確率が50%であることを確かめるために必要なサンプルサイズは、この誤差が許容できる水準を決めてしまえば自ずと決まります。
これを先ほどの例に当てはめてみます。これから送るメールのレス率がどのくらいなのかは、送ってみないことにはわかりませんが、「大数の法則」からレス率が許容誤差内に収まる適切なサンプルサイズが存在するであろう、ということは分かると思います。ただ、それを求める方法があるのか、、、、実はあるんです。
統計理論を応用すると、いくつかの条件を設定することで適切なサンプルサイズを計算できます。

テストパターン設計
いよいよテストパターン設計に入ります。ここが最も重要です。ABテストは2つ以上の施策を同時並行で実施し、どちらが効果があったかを統計的裏付けをもって検証する手法です。ポイントは3つあります。
① 比較するグループは無作為抽出する(グループ同士の属性を均質化)
均質な状態にしておかないと施策効果か属性の偏りによるものか判断できなくなるため
② 検証するに十分なサンプルサイズを設計して実施する
サンプルサイズが少ないと誤差が大きくなりすぎて検証・比較が不可能になるため
③ 比較する「違い」を1点に絞る
ABテストは1点の違いしか検証できないため
①②は説明してきましたので、③について具体的に説明します。
ABテストで検証できるのは1点の違いのみです。

上図のように、両施策の違いが1つだからこそ、効果の差はその違いによるものだといえるわけです。

もし、上図のように違いが2点(■と▲)あった場合、この場合では■+▲の影響で+1%ということはわかりますが、■と▲のそれぞれがどのくらい影響しているのかはわからなくなります。例えば、広告において画像を変えたことによる効果検証がしたいのに、キャッチコピーも変えたりすると、どっちがどう影響しているかわからなくなるわけですね。意図的にそうするのは問題ないですが、そうではないなら「違いは1点にする」という基本を押さえておきましょう。
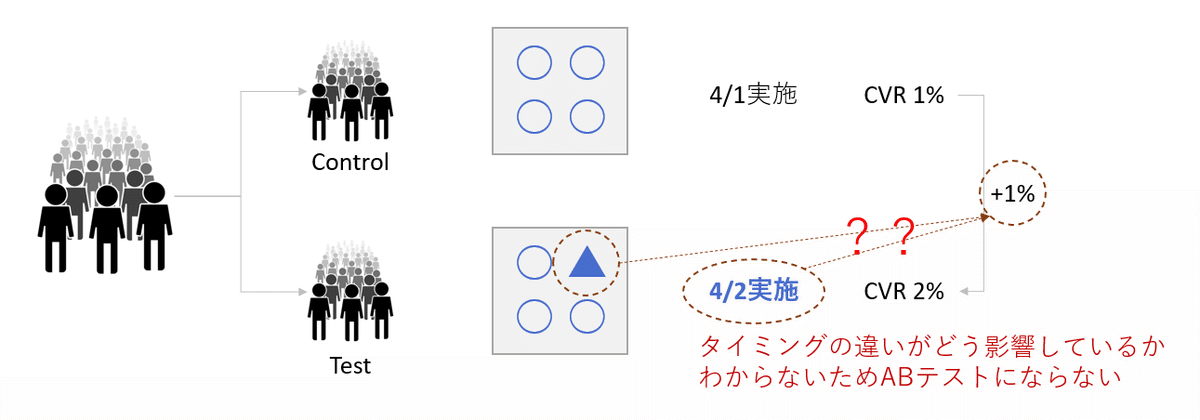
ちなみに、あえて同じ施策をタイミングをずらすABテストもあります(タイミングテスト)例えばメールマーケティングでは送信タイミングが午前・午後のどっちが反応がいいかをテストするといったことはあります。

これらのポイントを踏まえれば、複数のABテストも可能になります。この場合においても、必ず違いは1点となるようにパターンを設計する必要があります(パターンが増えるとサンプルサイズが不足したり、コストがかかったりするので注意)
有意差の検定
最後にABテストの結果の検証方法です(実はこれが一番難しいかも、、、、)実際にABテストによって得られた実績ですが、実測値は必ず誤差が生じます。
どういうことかというと、「大数の法則」でも触れましたが、サンプルサイズが小さいほど誤差が大きく、大きいほど誤差が小さいという法則があります。その性質を利用して、「想定される比率の予測値」「許容誤差」を指定してサンプルサイズを設計しているわけですが、あくまで予測値ですので実測値とは完全に一致しません。ここでサンプルサイズ設計の公式をみてみましょう。

この公式は「比率」「誤差」「サンプルサイズ」の3つの変数で成り立っています。テスト後においては「比率」「サンプルサイズ」は実績値であるため、それらをこの式に代入すると誤差が求められます。
例えばABテストによって以下のような結果が得られたとします。パターンAでは反応率p1、パターンBでは反応率p2、AよりもBの方が反応率が良いわけですが、本当にこれは「AよりもBの方が効果が高い」といえるのか?という話です。

さきほど説明した通り、実測値には誤差があります。もし、それぞれの誤差範囲が重なる場合、それは結果が逆転してしまう可能性があることを意味しています。

では「偶然ではない差」であるためには、誤差範囲が重ならないことが絶対条件になるのでしょうか? 答えはNOです。誤差範囲が重なっていても統計的に「偶然ではない」と判断できるケースがあります。
その判断をする手法として「統計的検定」というものがあり、この検定を行って差が「偶然ではない」という根拠付けを行うのですが、こちらについては別の記事で紹介しますので今回の説明は割愛させて頂きます。
ABテスト実施までの流れ
最後にこれまで説明してきたABテスト実施までの流れをまとめます。
1) ABテストの実施条件を言語化する
2) テストパターン設計
a) サンプルサイズ設計
b) ターゲットリストの抽出
c) 無作為抽出(ランダムサンプリング)
3) テスト実施⇨検証
1) ABテストの実施条件を言語化する
実施条件を明確にし、テストパターン設計を具体化します。

2) テストパターン設計
a) サンプルサイズ設計
想定される反応率、許容誤差から必要となるサンプルサイズを設計します。

b) ターゲットリストの抽出
ターゲットリストをデータベースから抽出します。

c) 無作為抽出(ランダムサンプリング)
ターゲットリストをテストするグループへ分割します。その際、無作為抽出によってランダム化し、(a)で求めたサンプルサイズ以上の数を確保できるように注意します。また、各グループへ実施するそれぞれの施策の「どの違い」を検証するのかを明確にして施策設計します。

3) テスト実施⇨検証
テストによって得られた結果(反応率の差異)が「偶然ではない差異」であることを統計的に検定を行います(今回は割愛)

いかがだったでしょうか?
ABテストは非常に有用な手法なので覚えておいて損はないと思います。
長文にお付き合い頂きありがとうございました。
