
PID制御とは?
この記事ではPID制御と呼ばれる、温度などの出力を制御する技術について解説を試みます。
実は最近のエスプレッソマシンには、お湯の温度を正確にコントロールするためにPID制御が使われているものがあります。お湯の温度はエスプレッソの味に多大な影響を与える要因の一つですので、それをコントロールすることは重要な課題でした。
エスプレッソマシン以外でもPIDを使っているものとして焙煎機や電気ケトルなどがあります。PIDまで使わなくても美味しいコーヒーは淹れれると思うのですが、こだわっていろいろ新しいモノを作ること自体が楽しいのかもしれません。

コーヒーの機器を例に挙げましたが、物理の実験機器にもPID制御は古くから使われています。本当に精密な温度制御が必要な場合には$${10^{-4}}$$から$${10^{-6}}$$K(ケルビン)という精度で制御をすることもあるそうです。
では、そんな偉大な技術の仕組みを解説していきましょう。僕自身の専門は制御理論などとはほとんど関係ないのですが、がんばって解説します。前提知識として高校数学(微分積分あたり)があるとわかりやすいと思います。
基本的な考え方
図のように、物体というのは入力に対して応答をして、出力がなされます。当たり前のように聞こえますが、この応答の性質を議論するだけでも本が一冊書けてしまうので、ここでは簡単に線形応答を仮定します。

時間$${t}$$の関数として、入力を$${x(t)}$$、出力を$${y(t)}$$とすると、線形応答をする物体では次のような関係(畳み込み)が成り立ちます。
$$
y(t) = \int_0^\infty g(t') x(t-t') dt'
$$
これをラプラス変換すると次のようになります。
$$
Y(s) = G(s) X(s)
$$
ここで関数$${f(t)}$$のラプラス変換を$${F(s) = \int_0^\infty f(t) e^{-st} dt}$$と定義しました。よくわからない場合は、ただこうやって書き換えておくと便利なんだなくらいで大丈夫です。実際、最初の式では積分で表されていたのがラプラス変換をかけるとただの掛け算で表されていることに気づくと思います。
制御の目標は、決められた出力ができるように、応答$${G(s)}$$をうまく設計することにあります。そのためにフィードバックという手法を使う必要が出てくるのです。フィードバックは図のように「応答を決めるためにその時点での出力を参照する」ということを意味します。
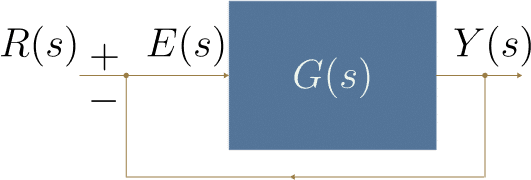
目標値:$${r(t)}$$
その時点での出力:$${y(t)}$$
その時点での誤差:$${e(t) = r(t) - y(t)}$$ (これが入力となる)
フィードバックの場合の入力は誤差$${e(t)}$$(ラプラス変換後は$${E(s)}$$と書く)であるので、入力と出力の関係を書くと、
$$
Y(s) = G(s) E(s)
$$
となります。ここから出力$${Y(s)}$$と目標値$${R(s)}$$の関係が
$$
Y(s) = \frac{G(s)R(s)}{1+G(s)}, \quad E(s) = \frac{R(s)}{1 + G(s)}
$$
となることがわかります。ここからすぐに$${G(s)}$$を大きくすれば$${Y(s)}$$と$${R(s)}$$が近くなるような気がしてきます。そこで、どのように$${G(s)}$$を決めたら素早く・正確に目標温度に到達するかということを考えることになります。
応答G(s)の決め方
さて、ここからは応答 $${G(s)}$$をどのように決めるかを説明するわけですが、その前にそもそもPIDが何の省略なのかを説明していませんでした。それぞれ以下の単語から来ています。
Proportional (比例)
Integral(積分)
Differential(微分)
つまりPID制御を日本語にすると「比例積分微分制御」になるわけです。必殺技の名前かな?
実はPID制御というのはその名の通り、応答$${G(s)}$$を、誤差$${E(s)}$$に比例する部分、積分・微分する部分の合計にしてしまうというものです。ではそれぞれの部分の働きについて見ていきましょう。
P:比例制御
比例制御の場合は入力の誤差$${E(s)}$$に比例するように出力$${Y(s)}$$をします。数式にすると次のようになります。
$$
Y(s) = K_p E(s)
$$
これは目標との差が大きければ大きいほど出力を大きくするというもので、とても自然な制御の方法だと言えます。しかし、この方法では誤差が0であるとき出力も0になってしまい、不安定な制御になってしまいます(鉛筆の尖った方を下にして立てないといけないような状況です)。温度を一定に保つために常に誤差が必要になり、いつまでも誤差が0にはなりません。これは以下のような計算で確かめられます。
$$
\lim_{t\to\infty} e(t) = \lim_{s\to0}sE(s) = \lim_{s\to0}\frac{sR(s)}{1 + G(s)} = \frac{1}{1+G(0)}
$$
ここで最初の等号でラプラス変換の「最終値の定理」を用い、目標値をステップ関数($${r(t) = 1, \; R(s) = 1/s}$$としました。今$${G(0) = K_p}$$なので、これが有限である限り誤差はいくら待っても0にならないことを意味しています。
I:積分制御
比例では不十分だということがわかったので、今度は次のような制御を考えてみます。
$$
y(t) = K_p e(t) + K_i \int_0^t e(t') dt' = K_p\left( e(t) + \frac{1}{T_i} \int_0^t e(t') dt'\right)
$$
$${K_i = K_p/T_i}$$としました。第2項が積分制御の部分で、これは以前までの誤差の積み重ね(積分)に対応して出力を決めることを意味しています。積分からの寄与を加えることで、現時点での誤差が0でも出力が0にならずに、より安定して制御できるようになります。
ラプラス変換の公式:$${\int_0^t f(t') dt' \to F(s)/s}$$を用いると上の式は次のように書き換えられます。
$$
Y(s) = K_p\left(1 + \frac{1}{T_i s} \right) E(s)
$$
D:微分制御
では最後に微分からの寄与を入れた場合を考えます。先ほど積分の寄与があるとより安定して制御ができるようになると言いましたが、積分の寄与は応答がある意味で「遅い」、言い換えると位相を後ろにずらすことに相当するので、すぐさま目標値に到達するには不利に働きます。そこで逆に位相を前にずらすことに相当する微分の寄与を入れることで、より素早く目標値に到達するようにします。
微分の寄与を加えた制御は次のようになります。
$$
y(t) = K_p e(t) + K_i\int_0^t e(t') dt' + K_d\frac{d e(t)}{dt} = K_p\left(e(t) + \frac{1}{T_i}\int_0^t e(t') dt' + T_d \frac{de(t)}{dt}\right)
$$
$${K_d = K_p T_d}$$です。これをラプラス変換の公式:$${df(t)/dt \to s F(s) }$$を用いて書き直すと、
$$
Y(s) = K_p \left( 1 + \frac{1}{T_i s} + T_d s \right) E(s)
$$
となります。微分制御はその瞬間の変化の大きさに対応して出力の大きさを決めるというもので、より迅速に目標値に近づける効果があります。
以上3つの要素からなる制御をまとめると次のように書くことができます。
$$
Y(s) = G(s) E(s),\quad G(s) = K_p\left(1 +\frac{1}{T_i s} + T_d s\right)
$$
これは$${G(0) = \infty}$$となり、時間無限大($${t\to\infty}$$)での誤差がきちんと0に行ってくれていることがわかります。実際の応用では上で出てきた定数($${K_p, T_i, T_d}$$)を制御したい物体に応じて決定して、最良の制御ができるように設計します。今は$${E(s)}$$と$${Y(s)}$$が制御装置$${G(s)}$$だけで結ばれているとしましたが、例えば物体が外界と接触することによる温度変化(熱が逃げるなど)を考慮して設計する必要が出てきます。
そもそもなんで積分とか微分を使って制御ができるのかというと、電子回路においてオペアンプというものを使えば簡単に電圧の積分や微分を出力する機構が作れるからです。(もちろん最近の機器はオペアンプなどの大きな部品は使っていませんが)
まとめ
以上でPID制御の簡単な説明はおしまいです。僕は思いました。PID制御って日常生活でもやってるなあって。
何か物事を決める時、「今の状況」「今までの経験」「それをした時に起こる変化」を考えたりすると思うのですが、これはまさに「比例」「積分」「微分」を考慮して次の行動を決めているっていうことですよね。まさにPIDの思考ですね。
もしかしたらいつかPIDをネタにしたトンデモ本が出るかもしれませんね。
※「最終値の定理」ってかっこよすぎないか。。。
