マイクラで100段のピラミッドを作る時に必要なブロックの数（解説）

問題はこちら：

答え：58219個

　健治君が建設しようとしているピラミッドに必要なブロックの総数は○○個になります。数え方は色々あると思いますが、まずは工夫した方法の一つを紹介し、その後で漸化式をベースにした計算式を求める方法を解説します。

解説1：ピラミッドを上から潰してみよう

　健治君が作ろうとしている100段の巨大ピラミッド。これをある高さの所で輪切りにした図をまずは見てみましょう：

　以後説明しやすいようにこの輪切り図を構成するブロックに名前を付けます。ピラミッドの外側となるブロックを辺ブロック、一段上のブロックの足場になる緑色のブロックを足場ブロックと呼ぶ事にします。

　では一番高い所にある頂点のブロックから順に輪切りにして、何かうまい方法が無いか検討してみましょう：

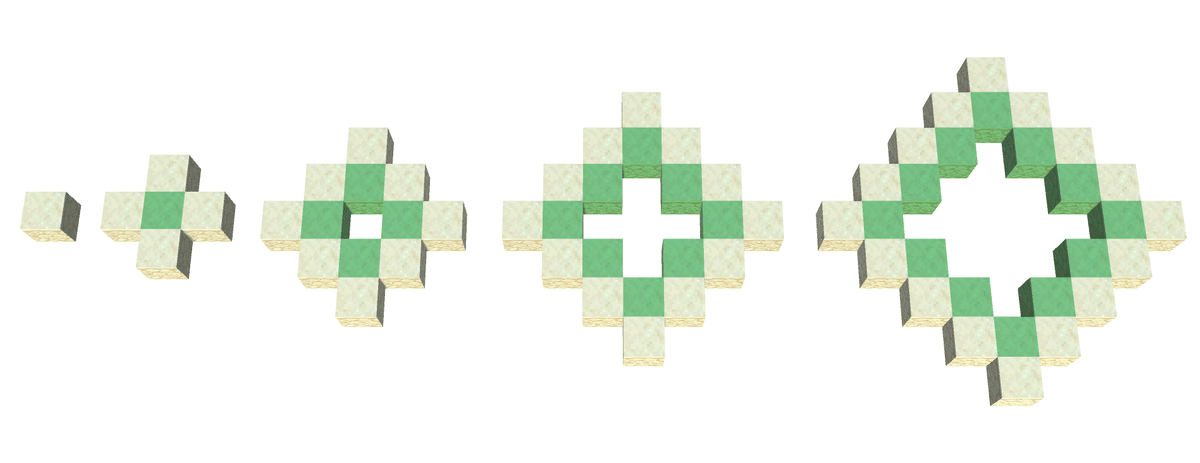
まずピラミッドの頂点には辺ブロックが1個だけあります。勿論足場ブロックはありません。
その下2段目で最初の足場ブロックが出現します。1段目用の足場ブロックが1つです。その上下左右に1個ずつ辺ブロックがくっつきます。
3段目は2段目の足場ブロック4個とその外側を包む8個の辺ブロックからなります。ここで初めて中空部が出現します。
4段目は3段目の足場8個とそれを外側から包む12個の辺ブロック。
5段目は足場ブロックが12個と辺ブロックが16個と増えていきます。
これが5段目以降も最下段の一つ前の99段目まで続きます。
最後100段目は底面になるので、外側と足場に加えてその内側もブロックで埋まります。底面だけはちょっと特別ですね。

　さて、ここで上図の緑の足場ブロックを一旦消して、辺ブロックだけに注目してみます。格段の辺ブロックを重ねて上から見てみましょう：

上図は見やすいように色分けしています。中心が1段目、その周りのオレンジなのが2段目…と重ねると、嬉しい事に綺麗に敷き詰められます。これは最下段である99段目まで同様に続けられますので、結局1～99段目までの辺ブロックは99段目の一辺が99個の正方形型の底面の個数と同じである事がわかります。

　次に緑の足場ブロックのみに注目してみましょう。1段目には足場ブロックがありませんが、2段目以降を見ると、これは辺ブロックとまったく同じピラミッド型になっているのがわかります！つまり上の重ね合わせができるんですね。ただし2段目が頂点、3段目が辺ブロックの2段目と同様…とその段数は辺ブロックより一つ下がります。つまり足場ブロックは1～99段あって、重ね合わせる事で98段目の正方形型底面の個数と一致するわけです。

　辺ブロックが99段目の正方形底面、足場ブロックが98段目の正方形底面の個数とそれぞれ同じになり、100段目にも正方形底面があります。ここからピラミッドで使われるブロックの個数は98～100段目の3段分の正方形底面の個数を数え上げれば求まるんです！

解説2：正方形底面の数え方

　正方形底面は100段目なら一辺が100個のブロックになっています。ただし斜めに配置されているので100×100ブロックというわけではありません。そういう正方形底面にあるブロックの個数を数える方法を検討するため、例として5段目の正方形底面で考えてみましょう：

5段目の正方形型底面は上図左のように5×5の塊と右図の4×4の塊に分ける事ができます。双方を重ね合わせると5段目の正方形底面になりますよね。つまり5段目の正方形底面の個数は、

このように求められます。段数×段数に(段数-1)×(段数-1)を足せば良いという事です。

解説3：ピラミッドのブロック数を求めよう

　解説1でピラミッドに使われるブロック数は98、99、100段目の正方形型底面の個数になる事を見てきました。そして解説2で正方形型底面の数え方もわかりました。これでブロック総数を求められますね。すなわち、

全部で58219個必要である事が分かりました。

　約6万個のブロックをマイクラの世界で集めて来るのはとても大変です。マイクラ経験者の方がイメージしやすい言い方をすれば、ラージチェスト17個分です。またその膨大なブロックをピラミッド型に並べて積み上げて行くのもこれまた大変な作業です。100段のピラミッドを作る健治君の計画…中々の作業になりそうですが、マイクラ民は何日かけてもやっちゃうんですよね～(^-^;。つまりマイクラ民にとってこれは「現実的」な規模ですww

深掘1：ブロック総数の一般化

　100段だけではなく任意の段数でのブロック数を求める式を作ってみましょう。と言ってもこれまでの解説でほぼ式が出来上がっていますので、それを記述するだけです。

　段数をmとした時、m段目の正方形型底面のブロック個数Nmは、

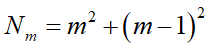
です。m段のピラミッドを作る時、ブロックの総数は下3段の正方形型底面の個数の和でした。ここからブロックの総数N(m)は、

このような2次方程式で計算できる事が分かります。上式にm=100を入れて計算すると解説で求めた58219個が出てきます。

深掘2：ピラミッドの中がみっちり詰まっていたら？

　健治君のピラミッドは中空でしたが、仮にこれが中までみっちりブロックで詰まっているピラミッドだったら、100段でどれだけのブロックが必要になるか計算してみましょう。

　深堀1にあるようにm段目の正方形底面の個数は、

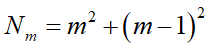
です。ブロックが詰まったピラミッドのm段目までのブロック総数をT(m)とすると、これはm=1～100までのNmの和になるので、

このようにΣで表現できます。上式を乗数で分類して整理すると、

上式で個数を求められる事がわかりました。100段だと…

約67万個にもなってしまいます！ラージチェスト194個分。ひえー。これは流石に現実的ではない規模かもしれません。

　中空で表面にブロックが並ぶ場合個数N(m)は2次関数でしたが、中までブロックが詰まっているT(m)は段数に対して3次関数となりました。これは「面積は2乗、体積は3乗」という概念ともちゃんと一致しています。面白いですよね。

　エジプトにあるギザの大ピラミッドなどは、今回の健治君のような斜めな正方形底面ではなくて将棋やチェス盤のようにマス目状に石を並べた底面になっています。その場合m段目の石の個数は単純にm²になるので、m段目までの総数は高校でならう2乗和の式そのままで、

となります。ちなみにギザの大ピラミッドは203段あるそうで、綺麗に石が並んでいるとした場合、m=203を上式に入れると約281万個と概算出来ます。実際は230万個ほどと推定されているようですが、それを人の手で積み上げたわけですから凄いですよね。

ではまた(^-^)/