30x6cmの箱は28x23cmの段ボール箱に入るか？（解説）

問題はこちら：

答え：入る！（高さ22.15cm）

　送りたい箱は、問題の段ボール箱に斜めに傾ける事で納める事が可能です。段ボール箱の高さが23cmなのに対して、斜めにした箱の上端までの高さは22.15cm。結構ギリギリです(^-^;

　実際僕がこれに直面した時も、段ボール箱や送る箱のサイズは問題とは異なりますが、神がかり的に高さギリギリセーフでしてほっとしたのを覚えています。

　この斜めにした箱の高さをどう求めるか？これが今回の問題の肝です。じっくり解説します。

解説：直角三角形の相似から方程式を立てよう

　送りたい箱が水平にも垂直にも入らないわけで、斜めに入れるしかない事はすぐにわかりますね。とすると必然的に送りたい箱の対角線が段ボール箱の側面に接する事になります（これ、後で重要になります）。そこで各辺の長さを以下のように文字で表してみます：

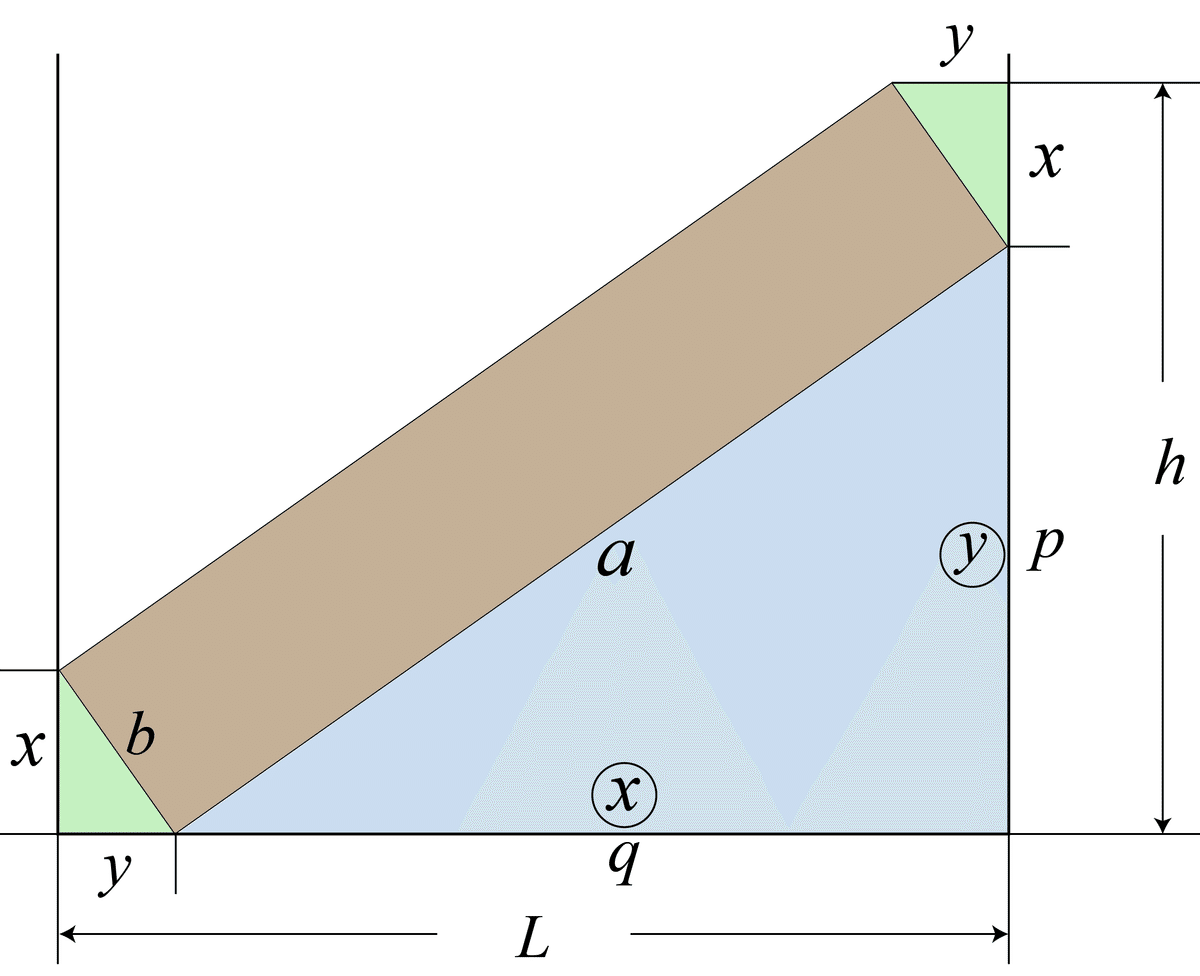
　段ボール箱の底辺の長さをLとします。また送る箱の長い方をa、短い方をbとします。これらは既知の値です。一方未知の値も定義しておきます。左隅に出来る小さな直角三角形の縦をx、横をyとし、青い三角形の高さをp、底辺をqとします。図には右上にも緑色の三角形がありますが、これは左下の緑色三角形と合同です。また緑と青の三角形は相似になっています。最終的に計算したい高さはhと表す事にします。

　まず高さhを他の文字で置き換える所から始めます。その為に青三角形の高さpを求めます。青三角形は唯一斜辺がaと分かっているので、同じく斜辺がbの緑三角形との相似比から、

ここからhは、

と書き表せます。式中にある定数値a/bですが、表記簡略のため以後

と置き換える事にします。

　高さhを求めるにはxとyが求まれば良い事がわかりました。そこで次に段ボール箱の底辺Lに注目します。図から、

です。qは先程と同様に青い三角形の相似比から、

です。ここから、

このようにyを底辺Lとxで書き表す事が出来ました。ところで、このyは緑色の直角三角形の1辺なので、三平方の定理から、

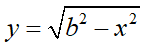
と表す事も出来ます。yについて2つ式が出来たので、等号で結んで整理すると、

このようなxについての2次方程式が導けます。x以外の値はすべて既知の定数なので、解の公式でxを解く事で具体的な長さが求まります。実際に展開してみましょう：

このようになります。式に±があるのでxが何故か2つ出て来る…これが意味する所は後述する事にして、とりあえず緑三角形の高さxが求まりました。ここから高さhを逆算します：

という事で高さhを段ボールの底辺の長さL、送る箱の縦幅aと縦幅bで計算する式が出来ました。まぁ…綺麗ではないですね(^-^;

　この式に今回の問題の条件であるL=28cm、a=30cm、b=6cmを代入すると、

2つの高さが算出されてきます。上が±のマイナス側、下がプラス側です。このどっちが欲しい高さなのか？これはxの値を求めて、それをy=L-rxの式に代入するとわかります。x、yはそれぞれ：

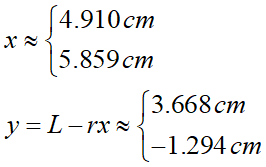
こう計算されます。結果yの下の方がマイナスになってしまいました。ここから上の(x,y)セットが妥当と分かります。よって送る箱の上端までの高さは22.15cmで段ボール箱の高さが23cmなので、無事収まる事がわかりました。

深掘：不採用側はいったい？

　今回採用したのはマイナス側の高さでした。では不採用だったプラス側の高さってそもそも何なのでしょうか？これはですね、以下の図をご覧下さい：

　斜めに入れる時に「送る箱の対角線が段ボールの側面に接する」というのが条件になっていました。冒頭で太文字にしていたあれです。送る箱には対角線が2つありますよね。正しい方は双方の対角線が段ボール内に収まります。でも上図のようにもう一方の対角線が段ボールの外に飛び出してしまうパターンが考えられまして、不採用側はこれだったんです。

　仮にxのプラス側を採用した場合にどこで矛盾が生じるか検証してみましょう。

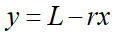
この関係式の右辺がマイナスになるかを調べます：

最終的に一番下のような関係式が出てきました。Lは段ボールの箱の底の長さで、aは送る箱の長い方の長さです。今回の問題ではL<aだったので、上式は成立しています。つまりxのプラス側を採用するとyが常にマイナス値になってしまうという事なので、こちらは常に不採用側になるわけです。

　今回の問題、僕が実際に箱を送ろうとして遭遇してしまった問題なのですが、僕は高さを知りたいのもありましたが、実は送る箱を下から支える青い三角形の形の緩衝材を段ボール板で作りたくて、チマチマと計算したというのが事の顛末です。スペースが広すぎて手元にあるプチプチが足りなくて青三角形型のスペーサーを作らざるを得なく、しかも送る箱を入れるとスペース部分が隠れて見えない…。だから青三角形の辺の長さを計算で求めるしかなかったんです(^-^;

　身近な思わぬ所でこういう計算が出て来た時にどうにかして答えを導く。そういうのが身を助ける事もあるという実例でした。ではまた(^-^)/