社会人のための学び直し数学【高校数学三角関数編その６】

6．加法定理②

　$${\mathrm{sin}x}$$ の加法定理を考えます。
前回は $${\mathrm{cos}x}$$ の加法定理

$${\mathrm{cos}(α-β)=\mathrm{cos}α\mathrm{cos}β+\mathrm{sin}α\mathrm{sin}β}$$　―(☆)

から始めましたが，今回もこの式から始めます。

　まずは準備から。

図 6-1

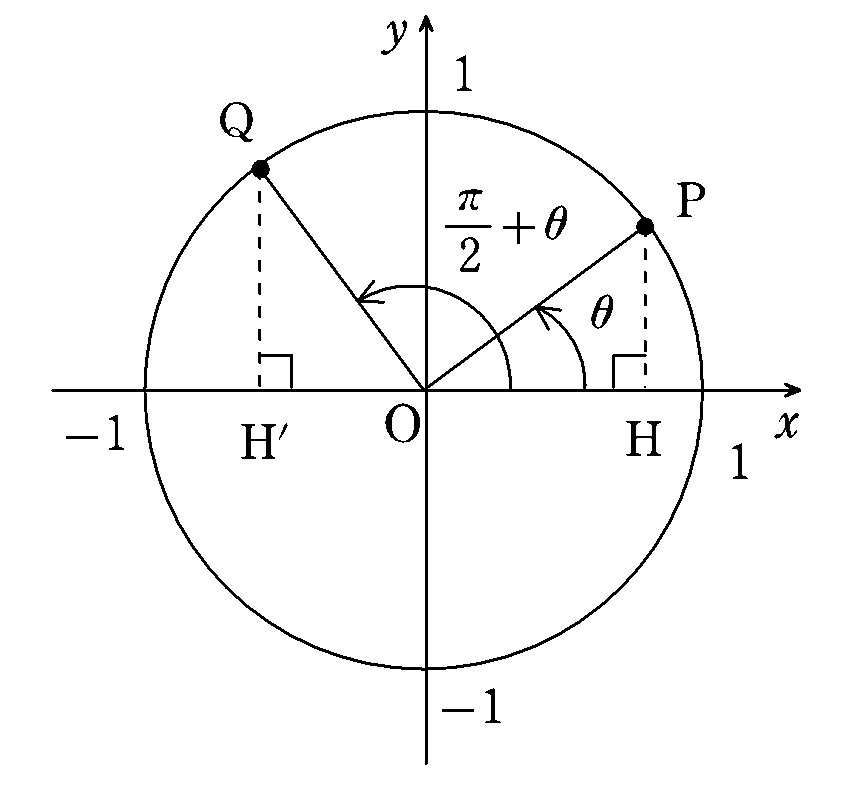
図 6-1 で動径 $${\mathrm{OP}}$$ および $${\mathrm{OQ}}$$ と $${x}$$ 軸の正の向きとのなす角をそれぞれ $${θ}$$，$${\cfrac{π}{2}+θ}$$ とし，円周上の点 $${\mathrm{P}}$$ および $${\mathrm{Q}}$$ から $${x}$$ 軸に下した垂線の足をそれぞれ $${\mathrm{H}}$$，$${\mathrm{H'}}$$ とします。
このとき点 $${\mathrm{P}}$$ の座標は

$${(\mathrm{cos}θ，\mathrm{sin}θ)}$$

点 $${\mathrm{Q}}$$ の座標は

$${\left(\mathrm{cos}(\frac{π}{2}+θ)，\mathrm{sin}(\frac{π}{2}+θ)\right)}$$

となります。また，$${△\mathrm{OPH}}$$ は $${\mathrm{OP}}$$ を斜辺とする $${∠\mathrm{POH}=θ}$$ の直角三角形で，$${y}$$ 軸の正の向きと動径 $${\mathrm{OQ}}$$ のなす角が $${θ}$$ であることに注意すれば，$${△\mathrm{OQH'}}$$ は $${\mathrm{OQ}}$$ を斜辺とする $${∠\mathrm{OQH'}=θ}$$ の直角三角形です。もちろん $${△\mathrm{OPH}}$$ と $${△\mathrm{OQH'}}$$ は合同な三角形です。すると，対応する辺の長さと，点 $${\mathrm{P}}$$，点 $${\mathrm{Q}}$$ の座標を見比べることで

$${\mathrm{cos}(\frac{π}{2}+θ)=-\mathrm{sin}θ}$$
$${\mathrm{sin}(\frac{π}{2}+θ)=\mathrm{cos}θ}$$

の成り立ちが確認できます。そして，点 $${\mathrm{P}}$$，点 $${\mathrm{Q}}$$ が円周上のどこにあっても $${∠\mathrm{POQ}=\cfrac{π}{2}}$$ が成り立つ限り，図 6-1 と同等の位置関係が動径 $${\mathrm{OP}}$$ および $${\mathrm{OQ}}$$ の間に見出せるので

$${\mathrm{cos}(\frac{π}{2}+θ)=-\mathrm{sin}θ}$$
$${\mathrm{sin}(\frac{π}{2}+θ)=\mathrm{cos}θ}$$

は一般に成り立ちます。
準備終了。

　加法定理 (☆) はどんな角 $${α，β}$$ に対しても成り立つので $${α}$$→$${\cfrac{π}{2}+α}$$ と書き換え，2 つの角 $${\cfrac{π}{2}+α}$$，$${β}$$ に対して書いてみると，

$${\mathrm{cos}(\frac{π}{2}+α-β)=\mathrm{cos}(\frac{π}{2}+α)\mathrm{cos}β+\mathrm{sin}(\frac{π}{2}+α)\mathrm{sin}β}$$

となります。すると，準備で説明した式を使って

$${\mathrm{cos}(\frac{π}{2}+α-β)=\mathrm{cos}\left(\frac{π}{2}+(α-β)\right)=-\mathrm{sin}(α-β)}$$
$${\mathrm{cos}(\frac{π}{2}+α)=-\mathrm{sin}α，\mathrm{sin}(\frac{π}{2}+α)=\mathrm{cos}α}$$

であるから

$${-\mathrm{sin}(α-β)=-\mathrm{sin}α\mathrm{cos}β+\mathrm{cos}α\mathrm{sin}β}$$

より

$${\mathrm{sin}(α-β)=\mathrm{sin}α\mathrm{cos}β-\mathrm{cos}α\mathrm{sin}β}$$

が導けます。
また，この式で $${β}$$ → $${-β}$$ と書き換え，

$${\mathrm{cos}(-β)=\mathrm{cos}β，\mathrm{sin}(-β)=-\mathrm{sin}β}$$

を使うと

$${\mathrm{sin}(α+β)=\mathrm{sin}α\mathrm{cos}β+\mathrm{cos}α\mathrm{sin}β}$$

も導けます。

　結局，$${\mathrm{cos}x}$$，$${\mathrm{sin}x}$$ の加法定理は

$${\mathrm{cos}(α-β)=\mathrm{cos}α\mathrm{cos}β+\mathrm{sin}α\mathrm{sin}β}$$　ー①
$${\mathrm{cos}(α+β)=\mathrm{cos}α\mathrm{cos}β-\mathrm{sin}α\mathrm{sin}β}$$　―②
$${\mathrm{sin}(α-β)=\mathrm{sin}α\mathrm{cos}β-\mathrm{cos}α\mathrm{sin}β}$$　―③
$${\mathrm{sin}(α+β)=\mathrm{sin}α\mathrm{cos}β+\mathrm{cos}α\mathrm{sin}β}$$　―④

の 4 つの式です。

　この 4 つの加法定理を使って，三角関数の公式をいくつか作ってみます。
①，③ で $${α=0}$$，$${β＝θ}$$ として，$${\mathrm{cos}0=1}$$，$${\mathrm{sin}0=0}$$ を使うと
　　$${\mathrm{cos}(0-θ)=\mathrm{cos}0\mathrm{cos}θ+\mathrm{sin}0\mathrm{sin}θ=\mathrm{cos}θ}$$
　　$${\mathrm{sin}(0-θ)=\mathrm{sin}0\mathrm{cos}θ-\mathrm{cos}0\mathrm{sin}θ=-\mathrm{sin}θ}$$
すなわち，$${\mathrm{cos}(-θ)=\mathrm{cos}θ}$$，$${\mathrm{sin}(-θ)=-\mathrm{sin}θ}$$ です。
①，③ で $${α=π}$$，$${β=θ}$$ として，$${\mathrm{cos}π=-1}$$，$${\mathrm{sin}π=0}$$ を使うと
　　$${\mathrm{cos}(π-θ)=\mathrm{cos}π\mathrm{cos}θ+\mathrm{sin}π\mathrm{sin}θ=-\mathrm{cos}θ}$$
　　$${\mathrm{sin}(π-θ)=\mathrm{sin}π\mathrm{cos}θ-\mathrm{cos}π\mathrm{sin}θ=\mathrm{sin}θ}$$
すなわち，$${\mathrm{cos}(π-θ)=-\mathrm{cos}θ}$$，$${\mathrm{sin}(π-θ)=\mathrm{sin}θ}$$ です。
②，④ で $${α=π}$$，$${β=θ}$$ として，$${\mathrm{cos}π=-1}$$，$${\mathrm{sin}π=0}$$ を使うと
　　$${\mathrm{cos}(π+θ)=\mathrm{cos}π\mathrm{cos}θ-\mathrm{sin}π\mathrm{sin}θ=-\mathrm{cos}θ}$$
　　$${\mathrm{sin}(π+θ)=\mathrm{sin}π\mathrm{cos}θ+\mathrm{cos}π\mathrm{sin}θ=-\mathrm{sin}θ}$$
すなわち，$${\mathrm{cos}(π+θ)=-\mathrm{cos}θ}$$，$${\mathrm{sin}(π+θ)=-\mathrm{sin}θ}$$ です。
②，④ で $${α=\cfrac{π}{2}}$$，$${β=θ}$$ として，$${\mathrm{cos}\cfrac{π}{2}=0}$$，$${\mathrm{sin}\cfrac{π}{2}=1}$$ を使うと
　　$${\mathrm{cos}(\frac{π}{2}+θ)=\mathrm{cos}\frac{π}{2}\mathrm{cos}θ-\mathrm{sin}\frac{π}{2}\mathrm{sin}θ=-\mathrm{sin}θ}$$
　　$${\mathrm{sin}(\frac{π}{2}+θ)=\mathrm{sin}\frac{π}{2}\mathrm{cos}θ+\mathrm{cos}\frac{π}{2}\mathrm{sin}θ=\mathrm{cos}θ}$$
すなわち，$${\mathrm{cos}(\frac{π}{2}+θ)=-\mathrm{sin}θ}$$，$${\mathrm{sin}(\frac{π}{2}+θ)=\mathrm{cos}θ}$$ です。

これらは，いままでに図を利用して導いた公式ですが，加法定理を使えば角度を書き換えるだけで導けるのです。

　さらに，公式をつくりましょう。
② で $${α=θ}$$，$${β＝θ}$$ とすると

$${\mathrm{cos}(θ+θ)=\mathrm{cos}θ\mathrm{cos}θ-\mathrm{sin}θ\mathrm{sin}θ＝\mathrm{cos}^2θ-\mathrm{sin}^2θ}$$

すなわち，$${\mathrm{cos}2θ=\mathrm{cos}^2θ-\mathrm{sin}^2θ}$$ です。
ここで，$${\mathrm{sin}^2θ=1-\mathrm{cos}^2θ}$$ あるいは $${\mathrm{cos}^2θ=1-\mathrm{sin}^2θ}$$ であることを使えば

$${\mathrm{cos}2θ=2\mathrm{cos}^2θ-1}$$ または $${\mathrm{cos}2θ=1-2\mathrm{sin}^2θ}$$

となります。これを $${\mathrm{cos}x}$$ の倍角の公式といいます。

④ で $${α=θ}$$，$${β＝θ}$$ とすると

$${\mathrm{sin}(θ+θ)=\mathrm{sin}θ\mathrm{cos}θ+\mathrm{cos}θ\mathrm{sin}θ＝2\mathrm{sin}θ\mathrm{cos}θ}$$

すなわち，$${\mathrm{sin}2θ=2\mathrm{sin}θ\mathrm{cos}θ}$$ です。これは $${\mathrm{sin}x}$$ の倍角の公式です。

$${\mathrm{cos}x}$$ の倍角の公式を $${\mathrm{cos}^2θ}$$ や $${\mathrm{sin}^2θ}$$ について解く（$${\mathrm{cos}^2θ}$$ や $${\mathrm{sin}^2θ}$$ を求める形にする）と

$${\mathrm{cos}^2θ=\cfrac{1+\mathrm{cos}2θ}{2}，\mathrm{sin}^2θ=\cfrac{1-\mathrm{cos}2θ}{2}}$$

となります。角度 $${2θ}$$ の半分の角度 $${θ}$$ を導いた形になっているので，これを半角の公式といいます。$${\mathrm{cos}x}$$ や $${\mathrm{sin}x}$$ を文字式のように見た場合の 2 次の形（2 乗したもの）が，1 次の形で表されているのがポイントです。

　このように，加法定理で角度を書き換えることで，三角関数のさまざまな公式を導くことができます。下の練習問題では 3 倍角の公式を導いてみましょう。

【練習問題】$${\mathrm{cos}3θ}$$ を $${\mathrm{cos}θ}$$ を用いて表せ。
［ヒント］② で $${α＝2θ}$$，$${β＝θ}$$ として，
　$${\mathrm{cos}2θ=2\mathrm{cos}^2θ-1}$$，$${\mathrm{sin}2θ=2\mathrm{sin}θ\mathrm{cos}θ}$$，$${\mathrm{sin}^2θ=1-\mathrm{cos}^2θ}$$
を使って変形する。

【答】$${\mathrm{cos}3θ=4\mathrm{cos}^3θ-3\mathrm{cos}θ}$$