
社会人のための学び直し数学【高校数学三角関数編その5】
5.加法定理①
前回までに,三角関数の正弦定理・余弦定理を見てきました。今回から 2 回にわたって三角関数の加法定理を考えます。一般に加法定理とは,関数 $${f(x)}$$ に関して $${f(x+y)}$$ を $${f(x)}$$ や $${f(y)}$$ で表す定理ですが,三角関数では $${\mathrm{cos}(x+y)}$$,$${\mathrm{sin}(x+y)}$$ 等を $${\mathrm{cos}x}$$,$${\mathrm{sin}x}$$,$${\mathrm{cos}y}$$,$${\mathrm{sin}y}$$ で表す定理になります。
最初に
$${\mathrm{cos}(α-β)=\mathrm{cos}α\mathrm{cos}β+\mathrm{sin}α\mathrm{sin}β}$$
から見ていきましょう。ここで $${0<α-β<π}$$ であるとします。
これは $${α-β}$$ を内角にもつ三角形を考えるためです。
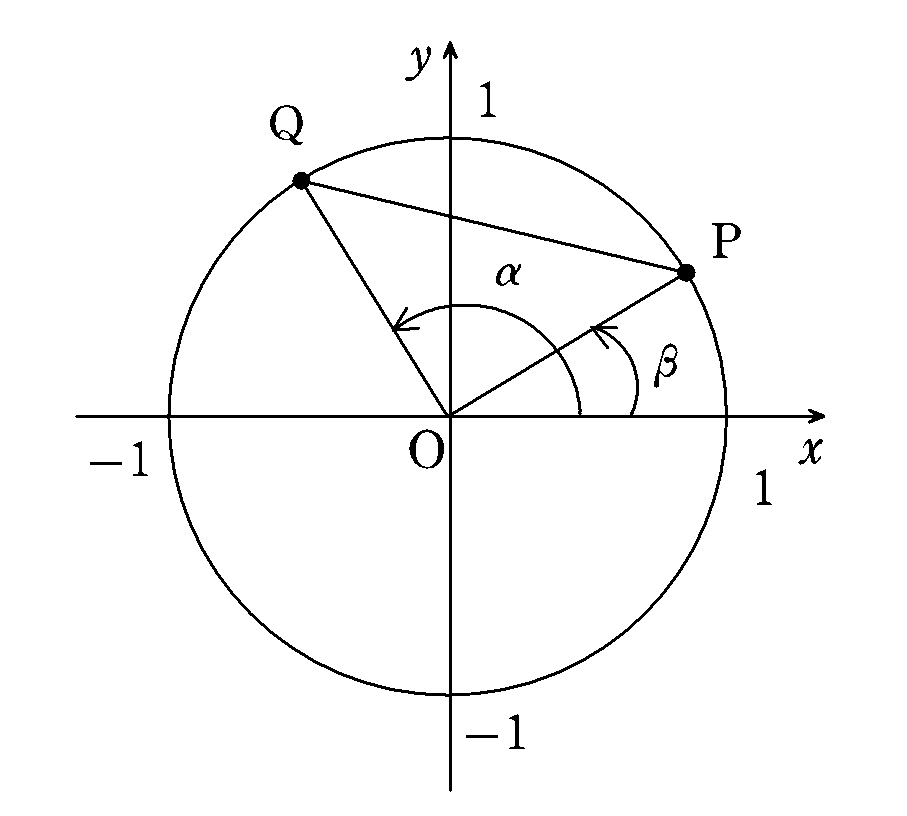
図 5-1 で点 $${\mathrm{P}}$$,点 $${\mathrm{Q}}$$ は単位円(半径が 1 の円)の円周上にあり,動径 $${\mathrm{OP}}$$ および動径 $${\mathrm{OQ}}$$ と $${x}$$ 軸の正の向きのなす角がそれぞれ $${β}$$,$${α}$$ なので三角関数の定義より,点 $${\mathrm{P}}$$ の座標は $${(\mathrm{cos}β,\mathrm{sin}β)}$$,点 $${\mathrm{Q}}$$ の座標は $${(\mathrm{cos}α,\mathrm{sin}α)}$$ となります。したがって,2 点 $${\mathrm{P}}$$,$${\mathrm{Q}}$$ 間の距離の 2 乗は
$${\mathrm{PQ}^2=(\mathrm{cos}α-\mathrm{cos}β)^2+(\mathrm{sin}α-\mathrm{sin}β)^2}$$
であり,$${\mathrm{cos}^2α+\mathrm{sin}^2α=1}$$,$${\mathrm{cos}^2β+\mathrm{sin}^2β=1}$$ を使えば
$${\mathrm{PQ}^2=2-2(\mathrm{cos}α\mathrm{cos}β+\mathrm{sin}α\mathrm{sin}β)}$$ ―①
です。
ところで,$${∠\mathrm{POQ}=α-β}$$ であり,$${0<α-β<π}$$ だったので $${△\mathrm{OPQ}}$$ が描けて,この三角形に余弦定理を適用すると
$${\mathrm{PQ}^2=1^2+1^2-2\mathrm{cos}(α-β)=2-2\mathrm{cos}(α-β)}$$ ―②
となります。
すると,①,② の右辺はともに $${\mathrm{PQ}^2}$$ の表現ですから
$${2-2(\mathrm{cos}α\mathrm{cos}β+\mathrm{sin}α\mathrm{sin}β)=2-2\mathrm{cos}(α-β)}$$
が成り立ち,結果
$${\mathrm{cos}(α-β)=\mathrm{cos}α\mathrm{cos}β+\mathrm{sin}α\mathrm{sin}β}$$ ―(☆)
です。
さらに,角度を広げることを考えます。そのための準備をしておきましょう。

図 5-2 で動径 $${\mathrm{OP}}$$ と $${x}$$ 軸に関して対称にとったのが動径 $${\mathrm{OP}'}$$ です。このとき動径 $${\mathrm{OP}}$$ と $${x}$$ 軸の正の向きとのなす角を $${θ}$$ とすると,動径 $${\mathrm{OP}'}$$ のなす角は必ず $${-θ}$$ となります。そして図からわかるように
$${\mathrm{cos}(-θ)=\mathrm{cos}θ}$$,$${\mathrm{sin}(-θ)=-\mathrm{sin}θ}$$
が一般に成り立ちます。また,動径 $${\mathrm{OP}}$$ と原点に関して対称にとったのが動径 $${\mathrm{OP}''}$$ です。このとき $${\mathrm{OP}}$$ と $${\mathrm{OP}''}$$ の間の角は必ず $${π}$$ となるので,図から分かるように
$${\mathrm{cos}(π+θ)=-\mathrm{cos}θ,\mathrm{sin}(π+θ)=-\mathrm{sin}θ}$$
が一般に成り立ちます。
また,$${\mathrm{cos}(π-θ)=-\mathrm{cos}θ}$$,$${\mathrm{sin}(π-θ)=\mathrm{sin}θ}$$ が成り立つことは前回で説明済みです。ただし,そのときの説明では $${0<θ<π}$$ と角度を制限しましたが,図を描くことで一般に成り立つことが確認できるでしょう。
以上で準備終了。
まず,$${α-β=π}$$ から見ていきましょう。このとき $${α=π+β}$$ なので (☆) の左辺は
$${\mathrm{cos}π=-1}$$
(☆) の右辺は
$${\mathrm{cos}(π+β)\mathrm{cos}β+\mathrm{sin}(π+β)\mathrm{sin}β}$$
=$${-\mathrm{cos}^2β-\mathrm{sin}^2β}$$
=$${-(\mathrm{cos}^2β+\mathrm{sin}^2β)=-1}$$
となり,(☆) は成り立っています。同様に左辺と右辺をそれぞれ変形することで $${α-β=0}$$,すなわち $${α=β}$$ のときも (☆) が成り立つことが確認できます。
次に,$${π<α-β<2π}$$ を見ていきましょう。
このとき,$${0<2π-(α-β)<π}$$ なので,2 つの角 $${π-α}$$ と $${-π-β}$$ については (☆) が成り立ちます。なぜなら
$${π-α-(-π-β)=2π-(α-β)}$$
となるからです。
よって,
$${\mathrm{cos}(2π-(α-β))=\mathrm{cos}(π-α)\mathrm{cos}(-π-β)+\mathrm{sin}(π-α)\mathrm{sin}(-π-β)}$$
です。この式を (※)式 としておきましょう。
ところで,三角関数はその定義上,任意の角度 $${α}$$ に対して,$${n}$$ を整数としたときに
$${\mathrm{cos}(α+2nπ)=\mathrm{cos}α,\mathrm{sin}(α+2nπ)=\mathrm{sin}α}$$
が成り立ちます。したがって
$${\mathrm{cos}(2π-(α-β))=\mathrm{cos}(-(α-β))=\mathrm{cos}(α-β)}$$
です。
また,$${\mathrm{cos}(π-α)=-\mathrm{cos}α,\mathrm{sin}(π-α)=\mathrm{sin}α}$$ であることと
$${\mathrm{cos}(-π-β)=\mathrm{cos}(-(π+β))=\mathrm{cos}(π+β)=-\mathrm{cos}β}$$
$${\mathrm{sin}(-π-β)=\mathrm{sin}(-(π+β))=-\mathrm{sin}(π+β)=\mathrm{sin}β}$$
を使うと (※)式 は (☆) と一致して $${π<α-β<2π}$$ での成立も示せました。
したがって,すべての角度 $${α}$$,$${β}$$ に対して
$${\mathrm{cos}(α-β)=\mathrm{cos}α\mathrm{cos}β+\mathrm{sin}α\mathrm{sin}β}$$ ―(☆)
が成り立つのです。
[参考]$${n}$$ を整数として $${\mathrm{cos}((α-β)+2nπ)=\mathrm{cos}(α-β)}$$ なので
$${0≦α-β<2π}$$ に対して成立することが示せれば十分です。
続いて
$${\mathrm{cos}(α+β)=\mathrm{cos}α\mathrm{cos}β-\mathrm{sin}α\mathrm{sin}β}$$
を見てみましょう。
これは (☆) において,$${β=-β}$$ とおき,
$${\mathrm{cos}(-β)=\mathrm{cos}β,\mathrm{sin}(-β)=-\mathrm{sin}β}$$
であることを使えば,すぐに確認できます。
まとめると,三角関数 $${\mathrm{cos}x}$$ の加法定理は
$${\mathrm{cos}(α-β)=\mathrm{cos}α\mathrm{cos}β+\mathrm{sin}α\mathrm{sin}β}$$
$${\mathrm{cos}(α+β)=\mathrm{cos}α\mathrm{cos}β-\mathrm{sin}α\mathrm{sin}β}$$
となります。
【練習問題】$${\mathrm{cos}\cfrac{π}{12}}$$ の値を求めよ。
[ヒント]$${\cfrac{π}{12}=\cfrac{π}{3}-\cfrac{π}{4}}$$ です。
【答】$${\cfrac{\sqrt{6}+\sqrt{2}}{4}}$$
いいなと思ったら応援しよう!

