
社会人のための学び直し数学【高校数学三角関数編その3】
3.正弦定理
単位円周上に点を取り,その点と原点を結んだ半径が $${x}$$ 軸の正の向きとなす角を $${θ}$$ とすると,点の座標は
$$
(\mathrm{cos}θ,\mathrm{sin}θ)
$$
と書けることが前回の内容でした。
今回,そして次回の 2 回の記事では $${θ}$$ を $${0≦θ≦π}$$ に限定し,図形の計量をおこなう上で強力な道具となる,2 つの定理を紹介します。
今回は正弦定理です。
準備として,中学数学で学習する円周角の定理を確認しておきましょう。(円周角の定理の証明については,中学数学の円周角に関する記事の中で取り上げます。)
次の図3-1で点 $${\mathrm{O}}$$ は円の中心,点 $${\mathrm{A,B,P}}$$ はそれぞれ円周上の点です。

点 $${\mathrm{A}}$$ から反時計回りに円周をなぞって点 $${\mathrm{B}}$$ に至る円周の一部を弧 $${\mathrm{AB}}$$ とし,弧 $${\mathrm{AB}}$$ を含まない円周上の任意の点を $${\mathrm{P}}$$ とすると,$${∠\mathrm{AOB}}$$ が弧 $${\mathrm{AB}}$$ に対する中心角,$${∠\mathrm{APB}}$$ が弧 $${\mathrm{AB}}$$ に対する円周角です。このとき,弧 $${\mathrm{AB}}$$ に対する中心角の大きさと円周角の大きさの間に $${∠\mathrm{AOB}=2∠\mathrm{APB}}$$ という関係が成り立ちます。これが円周角の定理です。まとめると「同じ弧に対する円周角は全て等しく,その大きさは中心角の半分になる」です。
もう一つ準備です。角度 $${θ}$$ の範囲を $${0<θ<\cfrac{π}{2}}$$ とし(この範囲の角度を鋭角といいます)て,三角関数 $${\mathrm{sin}θ,\mathrm{cos}θ}$$ と直角三角形との関連を確認しておきます。
角度 $${θ}$$ の範囲を $${0<θ<\cfrac{π}{2}}$$ の範囲に限るのであれば,座標平面の第 1 象限(座標平面上で $${x>0,y>0}$$ となっている部分)に,図3-2のような直角三角形を描くことができます。

この直角三角形を,辺の長さと三角関数 $${\mathrm{sin}θ,\mathrm{cos}θ}$$ の値がどのように関連するか,さらに角度 $${θ}$$ と三角関数 $${\mathrm{sin}θ,\mathrm{cos}θ}$$ との位置関係がどうなるのかがわかるように描いた図が図3-3です。
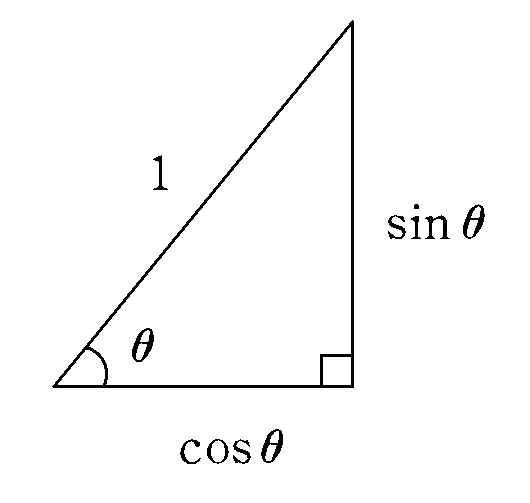
言葉で表現すれば,斜辺の長さが 1 の直角三角形では,その一つの鋭角 $${θ}$$ と向かい合う辺の長さが $${\mathrm{sin}θ}$$ で,鋭角 $${θ}$$ を挟んでいる斜辺でない方の辺の長さが $${\mathrm{cos}θ}$$ になるということです。
そして,角度 $${θ}$$ を固定して図3-3の直角三角形の斜辺の大きさを $${r}$$ 倍に拡大すれば,これは元の直角三角形と相似な直角三角形なので,斜辺以外も $${r}$$ 倍に拡大されて,図3-4の直角三角形になります。

言葉で表現すれば,斜辺の長さが $${r}$$ の直角三角形では,その一つの鋭角 $${θ}$$ と向かい合う辺の長さが $${r\mathrm{sin}θ}$$ で,鋭角 $${θ}$$ を挟んでいる斜辺でない方の辺の長さが $${r\mathrm{cos}θ}$$ になるということです。
それでは,正弦定理の説明に入りましょう。三角形の 3 つの頂点が全て円周上にあるとき,この三角形は円に内接するといい,円は三角形の外接円です。
ここで,図3-5のように,$${△\mathrm{ABC}}$$ の内部に外接円の中心がある場合を考えましょう。また,頂点 $${\mathrm{A}}$$ と向かい合う辺 $${\mathrm{BC}}$$ の長さを $${a}$$ とし,$${∠\mathrm{BAC}}$$ を単に $${A}$$ と書くことにします。さらに,外接円の半径を $${R}$$ であるとします。

そして,点 $${\mathrm{A}}$$ をこの位置から円周上で点 $${\mathrm{C}}$$ に向けて時計回りに,辺 $${\mathrm{BA}}$$ が円の中心を通るようになるまで回転させ,その位置を $${\mathrm{A}'}$$ としましょう。

すると,円周角の定理から $${∠\mathrm{BAC}=∠\mathrm{BA'C}=A}$$ であり $${∠\mathrm{A'OB}=π}$$(弧 $${\mathrm{A'B}}$$ に対する中心角)なので,$${∠\mathrm{A'CB}=\cfrac{π}{2}}$$(弧 $${\mathrm{A'B}}$$ に対する円周角)となります。
すなわち $${△\mathrm{A'BC}}$$ は直角三角形なので,$${a=2R\mathrm{sin}A}$$ が成り立ち(直角三角形で $${a}$$ が角 $${A}$$ と向かい合う辺の長さになっていて,斜辺の長さが $${2R}$$ となることに注意),
$$
\cfrac{a}{\mathrm{sin}A}=2R
$$
となります。
この関係は $${△\mathrm{ABC}}$$ の残りの 2 つの内角と,その内角に向かい合う辺についても,同様に考えることができるので,$${∠\mathrm{ABC}=B}$$,$${∠\mathrm{BCA}=C}$$,$${\mathrm{CA}=b}$$,$${\mathrm{AB}=c}$$ とすれば
$$
\cfrac{a}{\mathrm{sin}A}=\cfrac{b}{\mathrm{sin}B}=\cfrac{c}{\mathrm{sin}C}=2R……(☆)
$$
が成り立ちます。これが正弦定理です。
実は,ここまでの $${△\mathrm{ABC}}$$ は必ず鋭角三角形(3 つの角が全て鋭角になる三角形)なので,説明が不十分です。
$${A=\cfrac{π}{2}}$$,さらに $${\cfrac{π}{2}<A<π}$$(この範囲の角度を鈍角といい,一つの内角が鈍角の三角形を鈍角三角形といいます)となる場合について説明をします。
まず,$${A=\cfrac{π}{2}}$$ の場合ですが,これは $${△\mathrm{ABC}}$$ が $${\mathrm{BC}=a=2R}$$ を斜辺とする直角三角形であり,$${\mathrm{sin}\cfrac{π}{2}=1}$$ なので (☆) が成り立つことは問題ないでしょう。
$${\cfrac{π}{2}<A<π}$$ のときはどうでしょうか?
これには,一つ準備が必要です。$${\mathrm{sin}(π-θ)=\mathrm{sin}θ}$$ という公式を確認しましょう。

図3-7で動径 $${\mathrm{OP}}$$ の角度は $${θ}$$ で,動径 $${\mathrm{OP}}$$ と $${y}$$ 軸に関して対称な動径 $${\mathrm{OQ}}$$ の角度は $${π-θ}$$ となります。この図から一目瞭然,$${\mathrm{sin}(π-θ)=\mathrm{sin}θ}$$ です。さらに$${\mathrm{cos}(π-θ)=-\mathrm{cos}θ}$$ も読み取れるはずです。準備終わり。
[参考]角度 $${θ}$$ が $${\cfrac{π}{2}<θ<π}$$ となっているときは,図3-7の $${\mathrm{P,Q}}$$ の角度を入れ換えればいいので,上の結論に変化はありません。

図3-8で $${∠\mathrm{BAC}=A}$$ とすると,$${A}$$ は鈍角( $${\cfrac{π}{2}<A<π}$$ )であり,$${∠\mathrm{BA'C}=π-A}$$ となります。なぜなら,点 $${\mathrm{A}}$$ を含まない弧 $${\mathrm{BC}}$$ に対する中心角と,点 $${\mathrm{A'}}$$ を含まない弧 $${\mathrm{CB}}$$ に対する中心角の和は $${2π}$$ なので,$${∠\mathrm{BAC}+∠\mathrm{CA'B}}$$ という弧 $${\mathrm{BC}}$$,弧 $${\mathrm{CB}}$$ に対する円周角の和は $${π}$$ となるからです。(円に内接する四角形 $${\mathrm{ABA'C}}$$ の特徴の一つともいえます。)
すると $${△\mathrm{BA'C}}$$ は鋭角三角形で,前述の通り
$$
\cfrac{a}{\mathrm{sin}∠\mathrm{BA'C}}=2R
$$
となるのですが,$${\mathrm{sin}∠\mathrm{BA'C}=\mathrm{sin}(π-A)=\mathrm{sin}A}$$ なので,
$$
\cfrac{a}{\mathrm{sin}A}=2R
$$
となります。また,ほかの 2 つの角度は鋭角で,これは説明済みです。よって正弦定理 (☆) が成り立ちます。
ところで,三角形があれば,それは鋭角三角形,直角三角形,鈍角三角形のいずれかですから,すべての三角形に対して正弦定理が成り立つのです。
【練習問題】$${△\mathrm{ABC}}$$ において $${\mathrm{BC}=1}$$,$${\mathrm{CA}=\sqrt{2}}$$,$${∠\mathrm{ABC}=\cfrac{π}{4}}$$ のとき $${∠\mathrm{CAB}}$$ を求めなさい。
【答】$${\cfrac{π}{6}}$$
【解説】
$${∠\mathrm{BAC}=θ}$$ として,下の図の三角形に正弦定理を適用する。

正弦定理から $${\cfrac{1}{\mathrm{sin}θ}=\cfrac{\sqrt{2}}{\mathrm{sin}\cfrac{π}{4}}}$$
両辺の逆数をとって $${\mathrm{sin}θ=\cfrac{\mathrm{sin}\cfrac{π}{4}}{\sqrt{2}}=\cfrac{\cfrac{1}{\sqrt{2}}}{\sqrt{2}}=\cfrac{1}{2}}$$
よって,$${θ=\cfrac{π}{6}}$$
[注] $${\mathrm{sin}θ=\cfrac{1}{2}}$$ となるとき,$${θ=\cfrac{π}{6},\cfrac{5}{6}π}$$ が考えられますが,三角形の内角の和は $${π}$$ であることから,$${θ=\cfrac{5}{6}π}$$ はあり得ません。
いいなと思ったら応援しよう!

