社会人のための学び直し数学【高校数学三角関数編その４】

４．余弦定理

　今回は余弦定理です。
　斜辺の大きさが $${r}$$ の直角三角形と，その一つの鋭角 $${θ}$$ の三角関数 $${\mathrm{sin}θ}$$，$${\mathrm{cos}θ}$$ の値との関係は，図 4-1 で確認できるように鋭角 $${θ}$$ と向かい合う辺の長さが $${r\mathrm{sin}θ}$$ で，鋭角 $${θ}$$ を挟んでいる斜辺でない方の辺の長さが $${r\mathrm{cos}θ}$$ です。

図 4-1

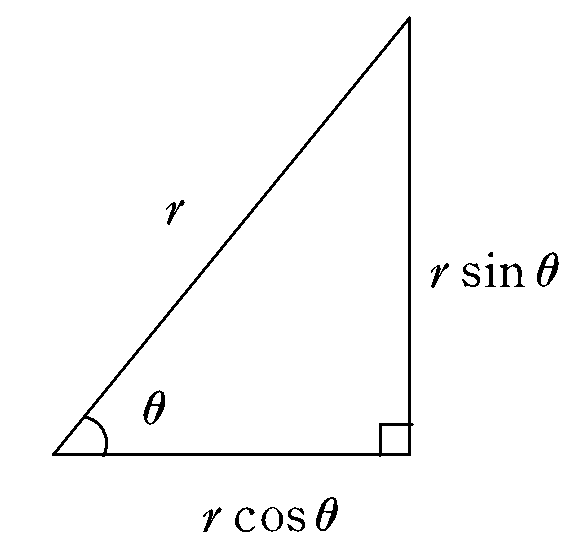
これを使うと，下の図 4-2 において

$${a=c}$$ $${\mathrm{cos}B+b}$$ $${\mathrm{cos}C}$$　―①

という式が導けます。

図 4-2

$${△\mathrm{ABC}}$$ の頂点 $${\mathrm{A}}$$ から辺 $${\mathrm{BC}}$$ に垂線 $${\mathrm{AH}}$$ を下ろし，$${\mathrm{BC}=a}$$，$${\mathrm{CA}=b}$$，$${\mathrm{AB}=c}$$ とし，頂点 $${\mathrm{A，B，C}}$$ での三角形の内角をそれぞれ $${A，B，C}$$ とします。すると直角三角形 $${\mathrm{ABH}}$$ で $${\mathrm{BH}}$$ は $${B}$$ を挟んでいる斜辺でない方の辺なので $${\mathrm{BH}=c}$$ $${\mathrm{cos}B}$$ であり，直角三角形 $${\mathrm{ACH}}$$ で $${\mathrm{CH}}$$ は $${C}$$ を挟んでいる斜辺でない方の辺なので $${\mathrm{CH}=b}$$ $${\mathrm{cos}C}$$ となります。よって，

$${a=\mathrm{BH}+\mathrm{CH}=c}$$ $${\mathrm{cos}B+b}$$ $${\mathrm{cos}C}$$

となって ① が成り立ちます。
そして，残りの頂点 $${\mathrm{B}}$$ や $${\mathrm{C}}$$ から向かい合う辺に垂線を下ろし，同様の考えから

$${b=a}$$ $${\mathrm{cos}C+c}$$ $${\mathrm{cos}A}$$　―②
$${c=b}$$ $${\mathrm{cos}A+a}$$ $${\mathrm{cos}B}$$　―③

が成り立ちます。
　ところで，図 4-2 のように頂点からその向かい合う辺に下した垂線の足（ここでは，垂線と辺の交点を垂線の足とよぶことにします）が辺上にある場合は，上述のとおりで納得できると思いますが，図 4-3 のように，垂線の足が辺の延長上にある場合はどうでしょうか。辺を延長する側の内角が鈍角になっている場合です。

図 4-3

図 4-3 では，辺の長さや角の表記は図 4-2 と同じとしますが，$${C}$$ が鈍角で $${\cfrac{π}{2}＜C＜π}$$ となっています。すると，

$${a=\mathrm{BH}-\mathrm{CH}}$$

であって，
　直角三角形 $${\mathrm{ABH}}$$ で $${\mathrm{BH}=c}$$ $${\mathrm{cos}B}$$
　直角三角形 $${\mathrm{ACH}}$$ で $${∠\mathrm{ACH}=π-C}$$ より $${\mathrm{CH}=b}$$ $${\mathrm{cos}(π-C)}$$
となっています。ところで前回 $${\mathrm{cos}(π-θ)=-\mathrm{cos}θ}$$ という公式を紹介しました。
したがって，
　$${a=c}$$ $${\mathrm{cos}B-b}$$ $${\mathrm{cos}(π-C)}$$
　　$${=c}$$ $${\mathrm{cos}B-(-b}$$ $${\mathrm{cos}C)}$$
　　$${=c}$$ $${\mathrm{cos}B+b}$$ $${\mathrm{cos}C}$$
であり，図 4-3 のような場合でも ① が成り立っていることがわかります。

［参考］$${C=\cfrac{π}{2}}$$ のときは $${\mathrm{cos}C=\mathrm{cos}\cfrac{π}{2}=0}$$ なので，この場合も ① は成立しています。

改めて，①～③ を書き出すと

$${a=c}$$ $${\mathrm{cos}B+b}$$ $${\mathrm{cos}C}$$　―①
$${b=a}$$ $${\mathrm{cos}C+c}$$ $${\mathrm{cos}A}$$　―②
$${c=b}$$ $${\mathrm{cos}A+a}$$ $${\mathrm{cos}B}$$　―③

となりますが，これを第一余弦定理といいます。

　さて，①～③ をもとにして，3 辺の長さが与えられた三角形で，三角関数の値を得る（ここでは特に $${\mathrm{cos}}$$ の値を得る）ための式を導いてみましょう。
三角関数は ①～③ の 3 つの式に，$${\mathrm{cos}A}$$，$${\mathrm{cos}B}$$，$${\mathrm{cos}C}$$ と 3 つあるので，これらの連立方程式として解けるはずです (未知数の数だけ式があれば，基本的には未知数が決定できます)。ここでは，$${\mathrm{cos}A}$$ を求める（3 つの式から $${\mathrm{cos}B}$$，$${\mathrm{cos}C}$$ を消去する）ことを考えましょう。
$${②×b-①×a}$$ より
　$${b^2-a^2=ab}$$ $${\mathrm{cos}C+bc}$$ $${\mathrm{cos}A-(ca}$$ $${\mathrm{cos}B+ab}$$ $${\mathrm{cos}C)}$$
ゆえに，

$${b^2-a^2=bc}$$ $${\mathrm{cos}A-ca}$$ $${\mathrm{cos}B}$$　―④

$${③×c+④}$$ より
　$${c^2+b^2-a^2=2bc}$$ $${\mathrm{cos}A}$$
よって，

$${\mathrm{cos}A=\cfrac{b^2+c^2-a^2}{2bc}}$$

と求められます。
$${\mathrm{cos}B}$$，$${\mathrm{cos}C}$$ についても同様に，

$${\mathrm{cos}B=\cfrac{c^2+a^2-b^2}{2ca}}$$

$${\mathrm{cos}C=\cfrac{a^2+b^2-c^2}{2ab}}$$

と求められます。
そして，これら 3 つの分母をはらって（分数の分母を式の両辺にかけて）少し整理すると

$${a^2=b^2+c^2-2bc}$$ $${\mathrm{cos}A}$$
$${b^2=c^2+a^2-2ca}$$ $${\mathrm{cos}B}$$
$${c^2=a^2+b^2-2ab}$$ $${\mathrm{cos}C}$$

となります。これが第二余弦定理です。普通，余弦定理といえばこちらの第二余弦定理を指していて，高校数学で学習する余弦定理は第二余弦定理のことです。
余弦定理（第二余弦定理）は三角形において，2 辺の長さと一つの角の値からもう一つの辺の長さを求めたり，3 辺の長さがわかっているときに三角関数の値を求めるため，ひいては内角の大きさを求めるために使います。

【練習問題】$${△\mathrm{ABC}}$$ において，$${\mathrm{BC}=1+\sqrt{3}}$$，$${\mathrm{CA}=2}$$，$${\mathrm{AB}=\sqrt{6}}$$ のとき $${∠\mathrm{ACB}}$$ の大きさを求めよ。

【答】$${∠\mathrm{ACB}=\cfrac{π}{3}}$$

【解説】$${△\mathrm{ABC}}$$ で $${\mathrm{BC}=a}$$，$${\mathrm{CA}=b}$$，$${\mathrm{AB}=c}$$，$${∠\mathrm{ACB}=C}$$ とすれば，余弦定理（第二余弦定理）の
　　$${\mathrm{cos}C=\cfrac{a^2+b^2-c^2}{2ab}}$$
から
　　$${\mathrm{cos}C=\cfrac{(1+\sqrt{3})^2+2^2-(\sqrt{6})^2}{2×(1+\sqrt{3})×2}}$$
となる。
これより
　　$${\mathrm{cos}C=\cfrac{4+2\sqrt{3}+4-6}{4(1+\sqrt{3})}}$$
すなわち
　　$${\mathrm{cos}C=\cfrac{2(1+\sqrt{3})}{4(1+\sqrt{3})}=\cfrac{1}{2}}$$
となる。よって，$${∠\mathrm{ACB}=C=\cfrac{π}{3}}$$ である。