#25 ポアソン分布の平均と分散の導出

こんにちは、まりなです。もう５月も終わりですね。つまり一年の5/12が終わるということです。分数にしてみましたが余計にわかんなくなっちゃいました。
先月末から今月初頭にかけてはGW毎日更新をなんとか達成出来たのですが、実は最終日上げた記事(オンライン授業のやつ)は本来ボツにする予定の記事でした。先輩風吹かしてる自分がなんか嫌だったので。この記事が本来最終日上げる予定だった記事なのですが最終日書いてる途中証明にミスを見つけて直すのが面倒になったので仕方なくボツにしかけてたあの記事を上げました。
まあでもフォロー外からもいいね貰えたし上げてよかったかな、どんな人がいいね押してくれたんだろうと見にいってみるとオンラインサロンとか経営コンサル系のアカウントで、#大学生 をつけても大学生に読んでもらえる訳では無いという学びを得ました。

本題に移りまして、確率論の話です。去年の後期厳しい確率論の講義あったなーと思い出し、復習がてら裳華房の統計学の教科書を読み返しながら、ネタになりそうな内容を探しているとポアソン分布の性質について面白いものがあったのでこれを記事にしました。

そういえばそんなのあったなと思いつつどう証明するのか回顧しました。

そもそもポアソン分布とは?

「試行回数が十分多く、確率pが十分小さい場合の二項分布」とよく紹介されます。二項分布はじゃあ何っていうと高校数学にも出てくる反復試行の確率のことですね。

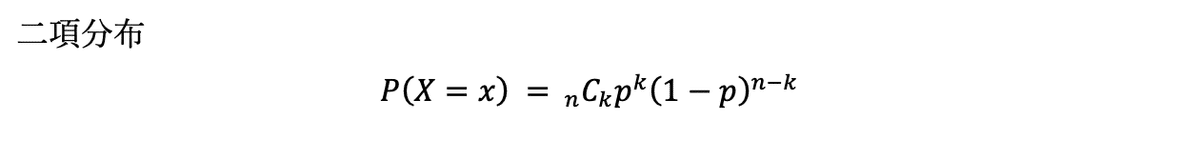
二項分布の式においてnp=λ(定数)とおいてn→∞(試行回数を十分多く), p→0(確率pを十分小さく) とするとポアソン分布が得られます。

平均・分散の基礎知識

「平均」はいわゆる期待値のことで「サイコロの出目の期待値は3.5」なんてよく言いますよね。これの計算式は (1+2+3+4+5+6)÷6 だと思っている方が多いと思いますが、平均(期待値)の厳密な定義に沿えば (1 * 1/6 + 2 * 1/6 + 3 * 1/6 + ・・・+6 * 1/6) となります。各「重み」(サイコロでは出目)にその確率(普通のサイコロならどの目も1/6ですね)をかけた値の和です。安いサイコロは重心が中心からずれているので本当は出目の期待値は3.5からずれているでしょうね。
確率論ではよくE(X)のように表します。

「分散」は高校数学でよく「データの散らばり具合」と習うかと思います。定義は教科書にのってるあの式

そしてよく知られた性質「２乗の平均ー平均の2乗」があるんでしたね。

分散は確率論ではV(X)のように表します。よってこの性質を確率論らしく書くとこうなります。

じゃあポアソン分布で計算してみよう

ポアソン分布でのkについての平均E(N)を求める過程を示します。サイコロ場合出目が6つなので6項足し合わせるだけでよかったのですがポアソン分布におけるkは試行回数であるためその上限がありません。よって平均は級数になります。

ここでこの式を具体的に書き下すとこうなりますよね

k=0の項は0になるのであってもなくても同じです。なのでk=1から和をとるのと変わらないので

実はこれが一番伝えたかったことなので(確率論の試験勉強をしていたときこの操作を思いつくのに1時間くらいかかりました...)ここで終わりにしたいくらいなのですが続けます。P(N=k)を実際に代入して計算すると

ここもまあまあ大事な操作ですね。(λx)^kを(λx)・(λx)^(k-1)とみなして分離します。すると級数の部分にk-1の形が多く出てきます。k=1からの和になっていますがk=0からに戻してこう書き換えられますね

すると級数の部分はe^(λx)のテイラー展開と全く同じ形になりました。よって

分散も導出してみます。「2乗の平均ー平均の２乗」を使いたいので2乗の平均E(N^2)を求めようとするのですがこれは計算できません。どうしてもkが残っていしまいます。ではどうするのかというとE(N(N-1))を計算します。

E(N)の場合と同様の手法で計算していくとまたE(N)の形が現れました。よって

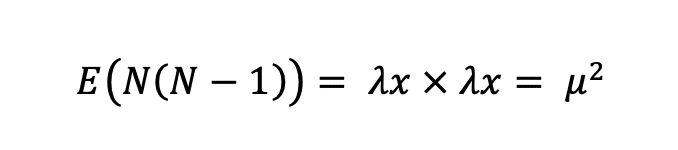
こうしてE(N(N-1))は意外とあっさり求められるのですが欲しかったのはE(N^2)でしたね。どうやってE(N^2)を得るのかというと、実は平均には線形性があります。あまり意識したことがないかと思いますがよく使っている技術です。中学生でも使っています。例えば151.5cm, 153.9cm, 149.3cm, 147.2cmのような身長のデータの平均を計算する時どうやって計算しますか。(151.5 + 153.9+・・・)÷4でも得られますが多くの人は「150cmを基準としたデータ[+1.5cm, +3.9cm, -0.7cm, -2.8cm]を作って平均を計算してその値に150cmを足す」という計算をするのではないでしょうか。これはまさに線形性を利用していますよね。数式で表すなら

E(h) = E(h'＋150) = E(h') + E(150) = E(h') + 150 

のようになり2式から3式への変形で確かに使っていますね。

よってE(N(N-1))は線形性を利用しE(N^2) - E(N)に変形できるのです。こうしてE(N^2)が得られます。

あとは「2乗の平均ー平均の２乗」するだけです。

となり、やっぱり分散もμでした。不思議ですね。

以上です。いかがでしたでしょうか。内容がニッチすぎかと思いましたが確率論に苦しめられている大学生は少なくないと思いまとめてみました。一助になれば幸いです。

それでは、最後まで読んでいただきありがとうございました。

P.S. もうお気づきの方もいらっしゃるかもしれませんが「スキ」を押すとランダムで鳥貴族のメニューが出るようにしました。よかったら押してみてください。