
【Blender Python】ガンマ関数を描く
ガンマ関数とは、階乗の概念を複素数全体に拡張した関数です。
Python には math ライブラリに gamma 関数がありますが、実数の正の値しか引数に取ることができません。
前回 Blender 内蔵の Python にインストールした SciPy ライブラリには複素数全体を引数に取れる gamma 関数があり、計算結果も複素数になります。
今回はこれを使ってガンマ関数を描画したいと思います。
Blender のバージョンは 2.93 LTS です。
1. ガンマ関数の絶対値
ガンマ関数の計算結果の複素数はそのままでは描画できないので、何らかの処理を行って実数にする必要があります。やり方には
・絶対値をとる
・実部をとる
・虚部をとる
の 3 種類があります。
まずは「絶対値をとる」からやってみましょう。
数式

コード
import numpy as np
import bpy
from scipy.special import gamma
# 既存要素削除
for item in bpy.data.meshes:
bpy.data.meshes.remove(item)
# x,y座標に応じてz座標を返す関数
def calc_z(x, y):
z = abs(gamma(x + 1j * y))
return(z)
# 分割数
x_len = 2000
y_len = 2000
# 範囲
x_min = -10
x_max = 8
y_min = -15
y_max = 15
lattice_x = np.linspace(x_min, x_max, x_len)
lattice_y = np.linspace(y_min, y_max, y_len)
verts = [[x, y, calc_z(x, y)] for y in lattice_y for x in lattice_x]
faces = [[x_len * y + x, x_len * y + x + 1, x_len * (y + 1) + x + 1, x_len * (y + 1) + x] for y in range(y_len - 1) for x in range(x_len - 1)]
msh = bpy.data.meshes.new("cubemesh") #Meshデータの宣言
msh.from_pydata(verts, [], faces) # 頂点座標と各面の頂点の情報でメッシュを作成
cube_obj = bpy.data.objects.new("cube_001", msh) # メッシュデータでオブジェクトを作成
bpy.context.scene.collection.objects.link(cube_obj) # シーンにオブジェクトを配置SciPy ライブラリから gamma 関数をインポートして、calc_z 関数内で使っています。
x 軸を実軸、y 軸を虚軸にしています。
実行結果

ガンマ関数の絶対値が描画できました。
3Dモデルなのでいろんな角度から見ることができますし、

このように裏側から見ることもできます。
この角度は他ではあまり見たことが無いんじゃないでしょうか。
2. ガンマ関数の実部
数式

コード
calc_z 関数の中身を
z = gamma(x + 1j * y).realに変えました。
実行結果

平行投影で横から見た図

横から見ると実数範囲のガンマ関数によく似た形が見えてきますね。

※ y = Γ (x) のグラフ(Wikipedia 「ガンマ関数」より)
平行投影で上から見た図

3. ガンマ関数の虚部
数式

コード
calc_z 関数の中身を
z = gamma(x + 1j * y).imagに変えました。
実行結果

実部の結果と似ていますね。
平行投影で横から見た図
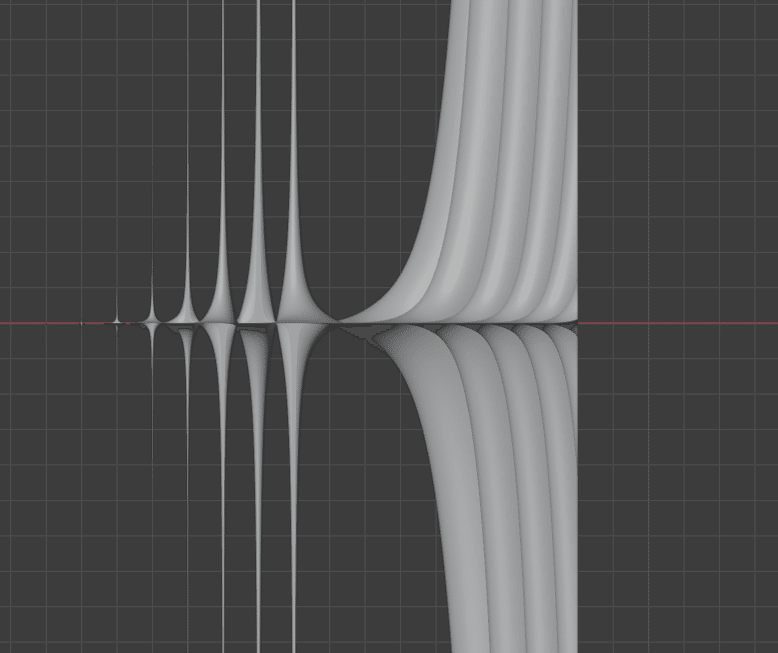
横から見ると実部の結果との違いがはっきりしますね。
平行投影で上から見た図

実部の結果と似ていますが、よく見比べると穴の形が違っていますね。
まとめ
SciPy ライブラリをインストールすることで出来ることが増えました。
他にもいろんなことをやっていきたいと思います。
