【数学】2次関数の解の配置

対象：定期試験以上

今回は　2次関数の解の配置問題(解の存在範囲)　の問題について学習しましょう

解の配置問題とは　2次関数で学ぶべき事項で
その後，3次方程式の概形に関わる問題や，三角・指数・対数等の関数の置き換えの場合，さらに領域等でも出てくる重要論点です

具体的な問題例としては

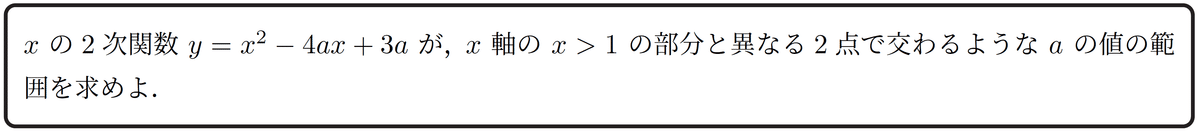
というようなもので，これら3つは表現が違いますが問題が同じです
よって，すべて解答が同じです

問題の条件が成り立つためには何が成り立てばよいか
を考え，連立不等式の問題となります
基本的には
判別式　　軸の位置　　端点の$${y}$$座標
を考えますが　その都度条件に合わせて考えましょう
上の問題は次の(i)の場合でした

他の頻出パターンも紹介します
「1個だけ」のときは　次の　(i)または(ii)　となります

ひとまとめにして　$${f(p)f(q)<0}$$　と表すこともできます

次は，2つ(重解含む)の場合で　(i)または(ii)となります

次は半直線上に少なくとも1個です

「少なくとも1個」を「2個のとき」「1個のとき」と場合分けしてもよいですが，軸の位置で場合分けしたほうがラクです．

文理問わず　国立大学2次等でよく出題されるのは次のものです

端点がうんぬん　が面倒なので　端点が解のときだけは特別扱いすればよいです

以上　解の配置問題のお話でした