【数学】集合の基礎理論

対象：定期試験以上

今回は　集合の基礎　について確認しましょう

条件を考えると　対応する集合を考えることができます
たとえば　「2の倍数」「自転車通学の人」などという条件を考えると
それぞれ集合ができますよね

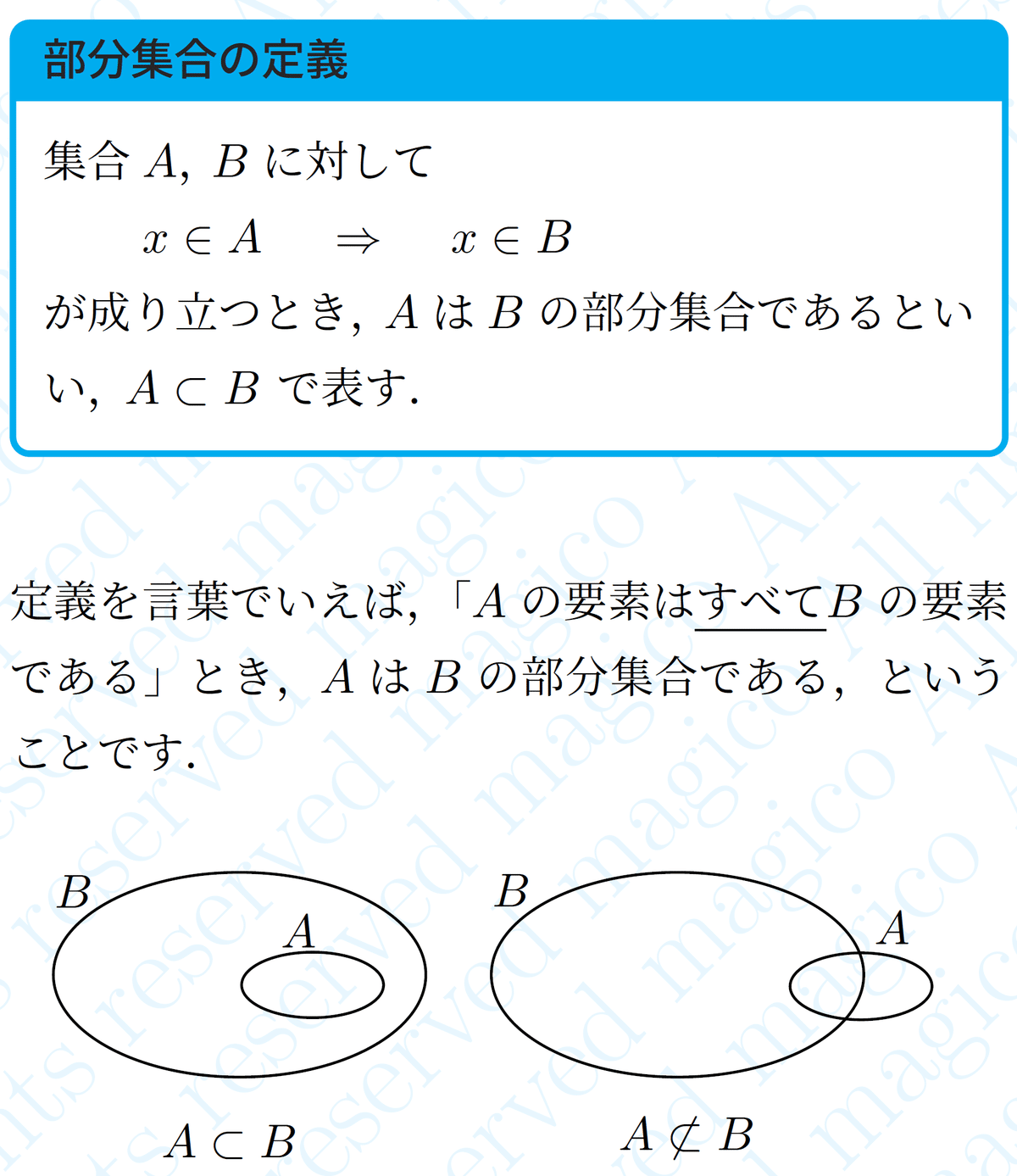
条件と集合は対応しているといいました
$${条件aを表す集合をA，条件bを表す集合をBとするとき}$$
　　　　$${「a \ \Rightarrow \ bが真」　\Leftrightarrow　「A\subset B」}$$
が成り立ちます

2つの集合が等しいことの言い換えです
「$${\subset}$$」の記号は　不等号で例えるなら等号付きの「$${\leqq ，\geqq}$$」と対応します
$${A\subset A}$$　は正しいです
自分自身も部分集合なんですね
全体と等しくなく，一部分であるという集合は真部分集合といいます

次は共通部分(積集合)　和集合についてです

そして　重要な分配法則

次は　空集合　補集合

空集合が任意の集合の部分集合となります

次の性質は記号ではなく意味で理解しましょう

最後に　ド・モルガンの法則(集合表現)　です

$${\overline{A\cup B}=\overline{A}\cap \overline{B}}$$　もベン図を描いて確かめてみてください