
【数学】共通接線02
対象:定期試験以上
前回に引き続き 共通接線の2回目 となります
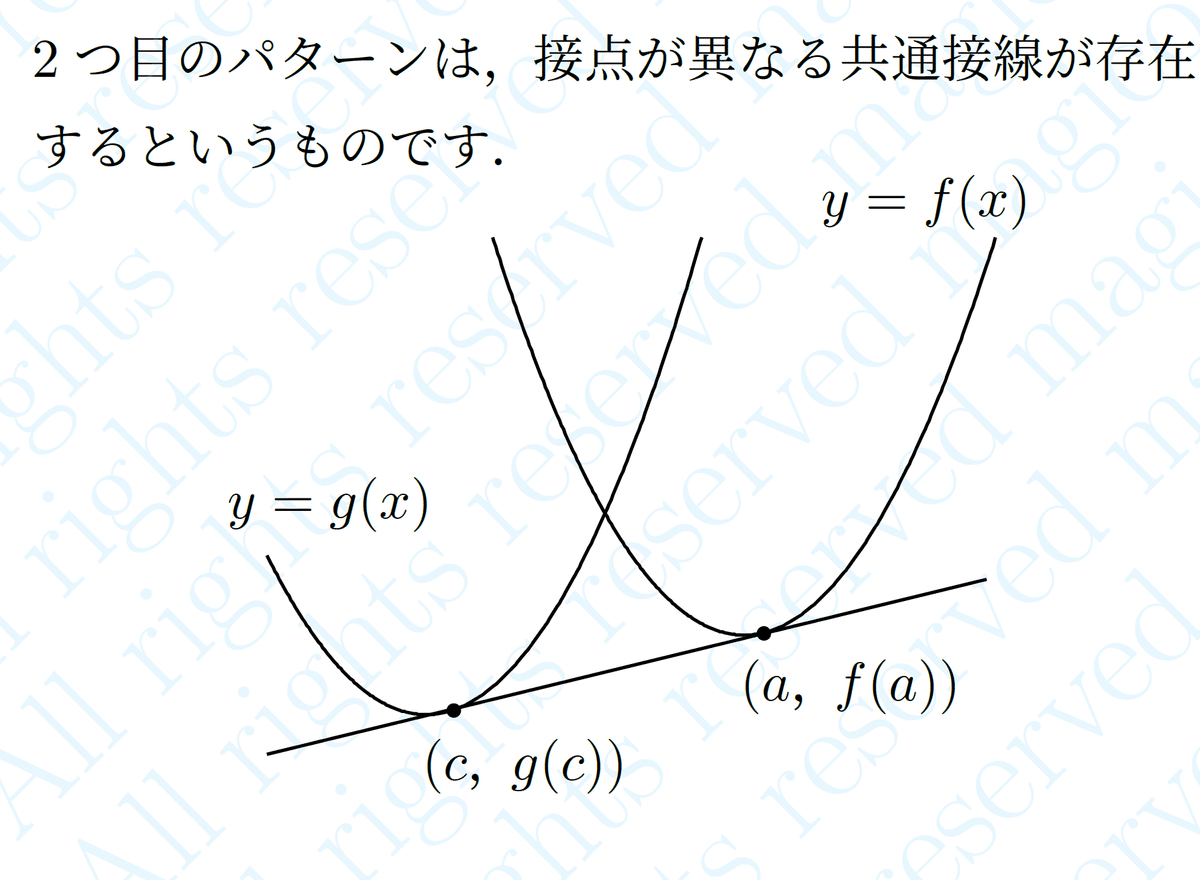
今回は 接点が異なる場合 についてです




上の2つ(I)(II)の解答とは異なり
共通接線を $${y=px+q}$$ と先において
双方と接すると考えて解くこともできます
接線$${y=px+q}$$が関数$${f(x)}$$と接する
$${\Rightarrow f(x)=px+q \ が重解をもつ}$$
を考えればよいですね
ただ 微分を利用して接線を先に作るほうが計算としてはラクです
さらに理系向けに話を続けると
この方法が利用できるのは$${f(x) \ が \ n \ 次関数や円などの2次曲線}$$の場合であり
理系の 数学IIIで様々な関数が出てきたときには 重解条件がつかえず
この議論が使えなくなります
そのときは 微分で接線を先つくる という
最初の(I)の方法となります
