【数学】区分求積法

対象：理系数学III

今回は　区分求積法　のお話です
極限が定積分と一致する　というアレですね
教科書にもあると思いますが　一応確認です

以上の2つをまとめると　結論として

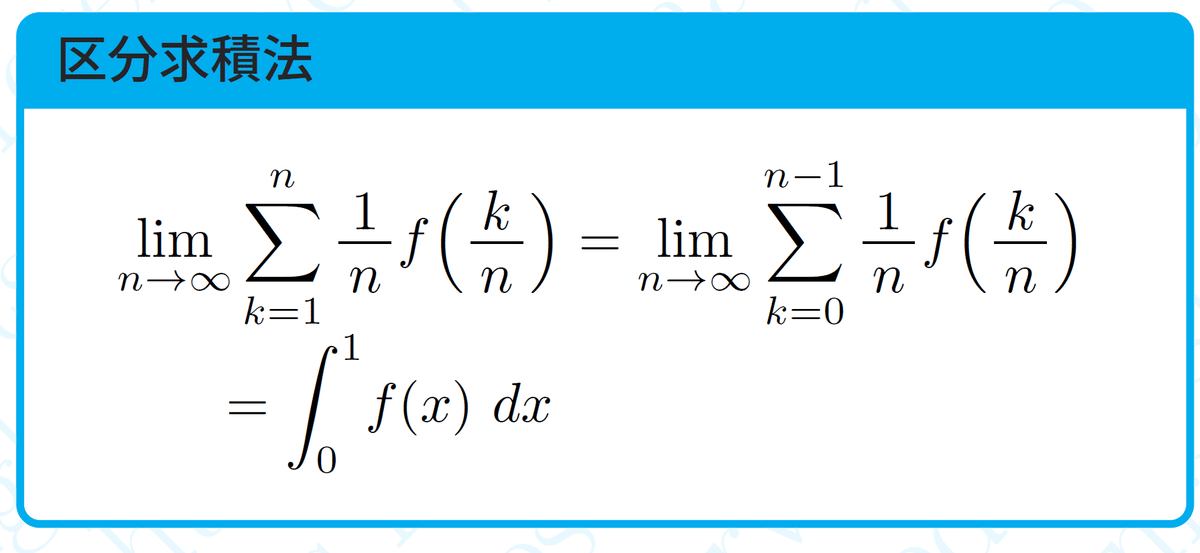
板1枚の幅が$${\dfrac{1}{n}}$$，枚数が$${n}$$枚というところが重要です

しかし，枚数がちょっとずれている(有限枚)程度では　極限には影響が出ません
例えば2枚多かったとすると

2枚の差は無視できるということです
さらに有限枚の差なら，どんなに大きくても無視できるところが
無限の面白いところ
10万枚増やしても　$${n\to \infty}$$　なら無視できます

$${n\to \infty}$$に対して　有限の値というのは無視できるんですね

ところが　$${n}$$枚増やして$${2n}$$枚になったのようなときには
話は変わってきます

板の幅が$${\dfrac{1}{n}}$$で$${2n}$$枚ですから
積分区間が$${[0，2]}$$となります
また，同じ$${n}$$枚であったとしても
スタートが違えば積分区間も変わってきますので注意

以上　区分求積法のお話でした